ABCD is square and CDE is an equilateral triangle outside the square. What is the value (in degrees) of ?
15
30
25
10
To solve the problem, we need to find the value of angle ∠BEC in the given configuration of a square ABCD and an equilateral triangle CDE outside the square.
1. Identify the Square and Triangle:
- Let ABCD be a square with each side of length X.
- Points C, D, and E form an equilateral triangle outside the square.
2. Determine the Angles in the Square:
- Since ABCD is a square, each angle in the square is 90∘.
- Therefore, ∠ABC=∠BCD=∠CDA=∠DAB=90∘.
3. Determine the Sides of the Equilateral Triangle:
- In the equilateral triangle CDE, all sides are equal. Thus, CD=DE=CE=X.
4. Calculate the Angles in the Equilateral Triangle:
- Each angle in an equilateral triangle measures 60∘.
- Therefore, ∠CDE=∠DCE=∠ECD=60∘.
5. Analyze Triangle BEC:
- In triangle BEC, we have:
- BC=X (side of the square)
- CE=X (side of the equilateral triangle)
- Thus, BC=CE, which means triangle BEC is isosceles with ∠CBE=∠CEB.
6. Calculate ∠CBE and ∠CEB:
- The sum of angles in triangle BEC is 180∘:
∠BEC+∠CBE+∠CEB=180∘
- Let ∠CBE=∠CEB=Y.
- Thus, we can write:
∠BEC+2Y=180∘
7. Determine Y:
- We know ∠ABC=90∘ and ∠CDE=60∘.
- Therefore, ∠CBE=90∘+60∘=150∘.
- Since ∠CBE+∠CEB=150∘, we have:
2Y=150∘⟹Y=75∘
8. Find ∠BEC:
- Substitute Y back into the equation:
∠BEC+2(75∘)=180∘
∠BEC+150∘=180∘
∠BEC=180∘−150∘=30∘
Final Answer:
Thus, the value of ∠BEC is 30∘.
---
- Let ABCD be a square with each side of length X.
- Points C, D, and E form an equilateral triangle outside the square.
- Since ABCD is a square, each angle in the square is 90∘.
- Therefore, ∠ABC=∠BCD=∠CDA=∠DAB=90∘.
- In the equilateral triangle CDE, all sides are equal. Thus, CD=DE=CE=X.
- Each angle in an equilateral triangle measures 60∘.
- Therefore, ∠CDE=∠DCE=∠ECD=60∘.
- In triangle BEC, we have:
- BC=X (side of the square)
- CE=X (side of the equilateral triangle)
- Thus, BC=CE, which means triangle BEC is isosceles with ∠CBE=∠CEB.
- The sum of angles in triangle BEC is 180∘:
∠BEC+∠CBE+∠CEB=180∘
- Let ∠CBE=∠CEB=Y.
- Thus, we can write:
∠BEC+2Y=180∘
- We know ∠ABC=90∘ and ∠CDE=60∘.
- Therefore, ∠CBE=90∘+60∘=150∘.
- Since ∠CBE+∠CEB=150∘, we have:
2Y=150∘⟹Y=75∘
- Substitute Y back into the equation:
∠BEC+2(75∘)=180∘
∠BEC+150∘=180∘
∠BEC=180∘−150∘=30∘
Thus, the value of ∠BEC is 30∘.
Topper's Solved these Questions
Similar Questions
In the given figure , ABCD is a square BCXYZ is a regular pentagon and ABE is an equilateral triangle . What is the value (in degrees) of ∠EBZ ?
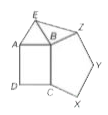
View SolutionIn the given figure, ABCD is a square, BCXYZ is a regular pentagon and ABE is an equilateral triangle. What is the value (in degrees) of ∠EBZ?
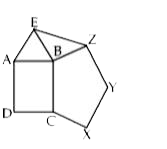
View Solution
Knowledge Check
ABCD is square and CDE is an equilateral triangle outside the square. What is the value (in degrees) of ∠BEC?
A15B30C25D10ABCD is a square and ABE is an equilateral triangle outside the square then
A∠ACE=12∠ABEB∠ACE=∠ABEC∠ACE=2∠ABEDNone of theseABCD is a square and AOB is an equilateral triangle. What is the value of ∠DOC?
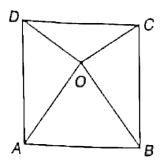 A120∘B150∘C125∘Dcan't be determined
A120∘B150∘C125∘Dcan't be determined
ABCD is square . BCE is equilateral Δ outside . Find ∠DEC
View SolutionABCD is a square. BEC is an equilateral triangle inside the square. If CE & BD intersects at O. Find ∠BOC=?
View SolutionABCD is a square and BCE is an equilateral triangle. Find the value of a,b and reflex ∠BED.
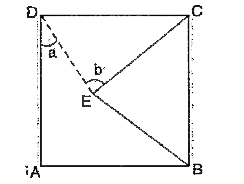
View SolutionIn the given figure, PQRS is a square and SRT is an equliateral triangle. What is the value (in digrees) of ∠SOR ?
View SolutionIn the given figure,ΔCDE is an equlatel triangle triangle formed on a side CD of a square ABCD.Show that ΔADE≅ΔBCE.
View Solution
