If AD, BE and CF are the medians of a ΔABC, then evaluate (AD2+BE2+CF2):(BC2+CA2+AB2).
The correct Answer is:(3:4)
To solve the problem of evaluating the ratio (AD2+BE2+CF2):(BC2+CA2+AB2), where AD, BE, and CF are the medians of triangle ABC, we can follow these steps:
1. Identify the sides of the triangle:
Let a=BC, b=CA, and c=AB.
2. Use the formula for the length of the medians:
The lengths of the medians can be expressed using the following formulas:
- AD=12√2b2+2c2−a2
- BE=12√2a2+2c2−b2
- CF=12√2a2+2b2−c2
3. Square the lengths of the medians:
- AD2=(12√2b2+2c2−a2)2=14(2b2+2c2−a2)
- BE2=(12√2a2+2c2−b2)2=14(2a2+2c2−b2)
- CF2=(12√2a2+2b2−c2)2=14(2a2+2b2−c2)
4. Combine the squared medians:
AD2+BE2+CF2=14((2b2+2c2−a2)+(2a2+2c2−b2)+(2a2+2b2−c2))
Simplifying this expression:
=14(4a2+4b2+4c2−(a2+b2+c2))
=14(3a2+3b2+3c2)=34(a2+b2+c2)
5. Calculate the sum of the squares of the sides:
BC2+CA2+AB2=a2+b2+c2
6. Form the ratio:
AD2+BE2+CF2BC2+CA2+AB2=34(a2+b2+c2)a2+b2+c2
Simplifying this gives:
=34
Final Result:
Thus, the required ratio is:
(AD2+BE2+CF2):(BC2+CA2+AB2)=34
Let a=BC, b=CA, and c=AB.
The lengths of the medians can be expressed using the following formulas:
- AD=12√2b2+2c2−a2
- BE=12√2a2+2c2−b2
- CF=12√2a2+2b2−c2
- AD2=(12√2b2+2c2−a2)2=14(2b2+2c2−a2)
- BE2=(12√2a2+2c2−b2)2=14(2a2+2c2−b2)
- CF2=(12√2a2+2b2−c2)2=14(2a2+2b2−c2)
AD2+BE2+CF2=14((2b2+2c2−a2)+(2a2+2c2−b2)+(2a2+2b2−c2))
Simplifying this expression:
=14(4a2+4b2+4c2−(a2+b2+c2))
=14(3a2+3b2+3c2)=34(a2+b2+c2)
BC2+CA2+AB2=a2+b2+c2
AD2+BE2+CF2BC2+CA2+AB2=34(a2+b2+c2)a2+b2+c2
Simplifying this gives:
=34
Thus, the required ratio is:
(AD2+BE2+CF2):(BC2+CA2+AB2)=34
Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - PROPERTIES AND SOLUTIONS OF TRIANGLES EXERCISE 7 : SUBJECTIVE TYPE QUESTIONS
10 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
21 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - PROPERTIES AND SOLUTIONS OF TRIANGLES EXERCISE 6 : SINGLE INTEGER ANSWER TYPE QUESTIONS
1 Video
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
51 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
If AD,BEandCF are the medians of a ΔABC,then(AD2+BE2+CF2):(BC2+CA2+AB2) is equal to
View SolutionIf AD,BEandCF be the median of a △ABC, prove that −−→AD+−−→BE+−−→CF=0
View SolutionIf D, E and F be the middle points of the sides BC,CA and AB of the ΔABC, then AD+BE+CF is
View SolutionIf G be the centroid of a triangle ABC, prove that, AB2+BC2+CA2=3(GA2+GB2+GC2)
View SolutionIn a triangle ABC,B=90∘ and D is the mid-oint of BC then prove that AC2=AD2+3CD2
View SolutionIn an acute angled triangle ABC, AD is the median in it. then :
AD2 =
View SolutionAD, BE and CF asre the medians of a triangle ASBC intersectiing in G. Show that △AGB=△BGC=△CGA=13△ABC.
View SolutionThe following figure shows a triangle ABC in which AD is a median and AE⊥BC. Prove that 2AB2+2AC2=4AD2+BC2 .
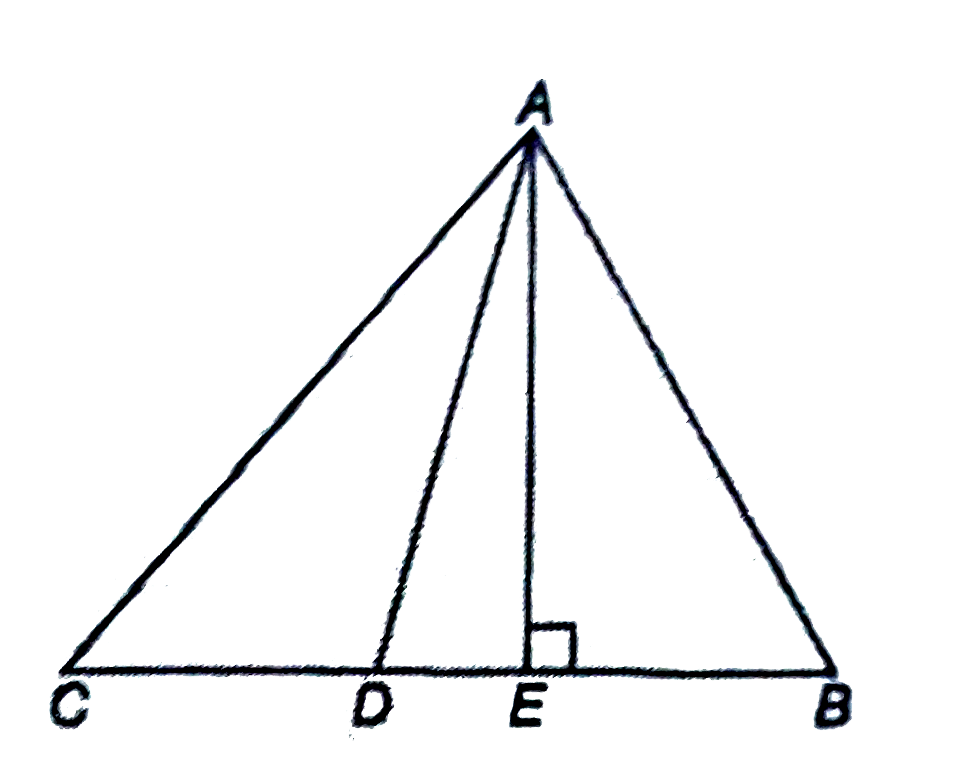
View SolutionLet AD be a median of the ΔABC. If AE and AF are medians of the triangle ABD and ADC, respectively, and BD=a/2 AD = m1,AE=m2,AF=m3, then a2/8 is equal to
View SolutionIf AD, BE and CF are the altitudes of ΔABC whose vertex A is (-4,5). The coordinates of points E and F are (4,1) and (-1,-4), respectively. Equation of BC is
View Solution