The great German naturalist and geographer Alexander von Humboldt observed that within a region species richness increased with increasing explored area, but only up to a limit. In fact, relation between species richness and area for a wide variety of taxa (angiosperm plants, birds, bats, freshwater fi ishes) turns out to be a rectangular hyperbola. Now find out correct equations shown in the graph.
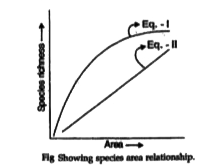
I - S−CAZ II -LogS=logC+ZlogA
I - LogS=logC+ZlogA, II - S−CAZ
I - S−CAZ+logC, II - LogS=logC+ZlogA
I - S−CAZ+logA, II - LogS=logC+ZlogA
The correct Answer is:A
Similar Questions
The relation between species richness and area for a wide variety of taxa (angiosperm plants, birds, bats, freshwater fishes) is a
View SolutionThe graph formed by plotting species richness against area for a wide variety of taxa (angiosperm plants, birds , bats , fresh water fishes , etc) turns out to be a
View Solution
Knowledge Check
The relation between species richness and area for a wide variety of taxa (angiosperm plants, birds, bats, freshwater fishes) is a
AParabolaBRectangular hyperbolaCEllipseDStraight lineThe graph formed by plotting species richness against area for a wide variety of taxa (angiosperm plants, birds , bats , fresh water fishes , etc) turns out to be a
AparabolaBstraight lineCRectangular hyperbolaDAny of the aboveWhich of the statement are in accordance with the observation of geographer Alexander von Humboldt ?
I. Within a region species, richness increases with increasing explored area but within a limit.
II. The relation between species richness and area is a rectangular hyperbole.
III. The richness of species decreases with the increasing explored area.
IV. There is no relation between the explored area and species richness .AI and II onlyBI , III and IVCII and IVDII and III
The relation between species richness and area for a wide variety of taxa turns out to be a rectangular hyperbola. Give a brief explanation.
View SolutionThe relation between species richness and area for a wide variety of taxa turns out to be a rectangular hyperbola. Give a brief explanation.
View SolutionWhich of the statement are in accordance with the observation of geographer Alexander von Humboldt ?
I. Within a region species, richness increases with increasing explored area but within a limit.
II. The relation between species richness and area is a rectangular hyperbola.
III. The richness of species decreases with the increasing explored area.
IV. There is no relation between the explored area and species richness .
View SolutionAlexander von Humboldt gave the relationship between the species richness and its geographical area . Which of the following is the correct logarithmic equation for his findings ?
View SolutionAlexander von Humboldt gave the relationship between the species richness and its geographical area . Which of the following is the correct logarithmic equation for his findings ?
View Solution
