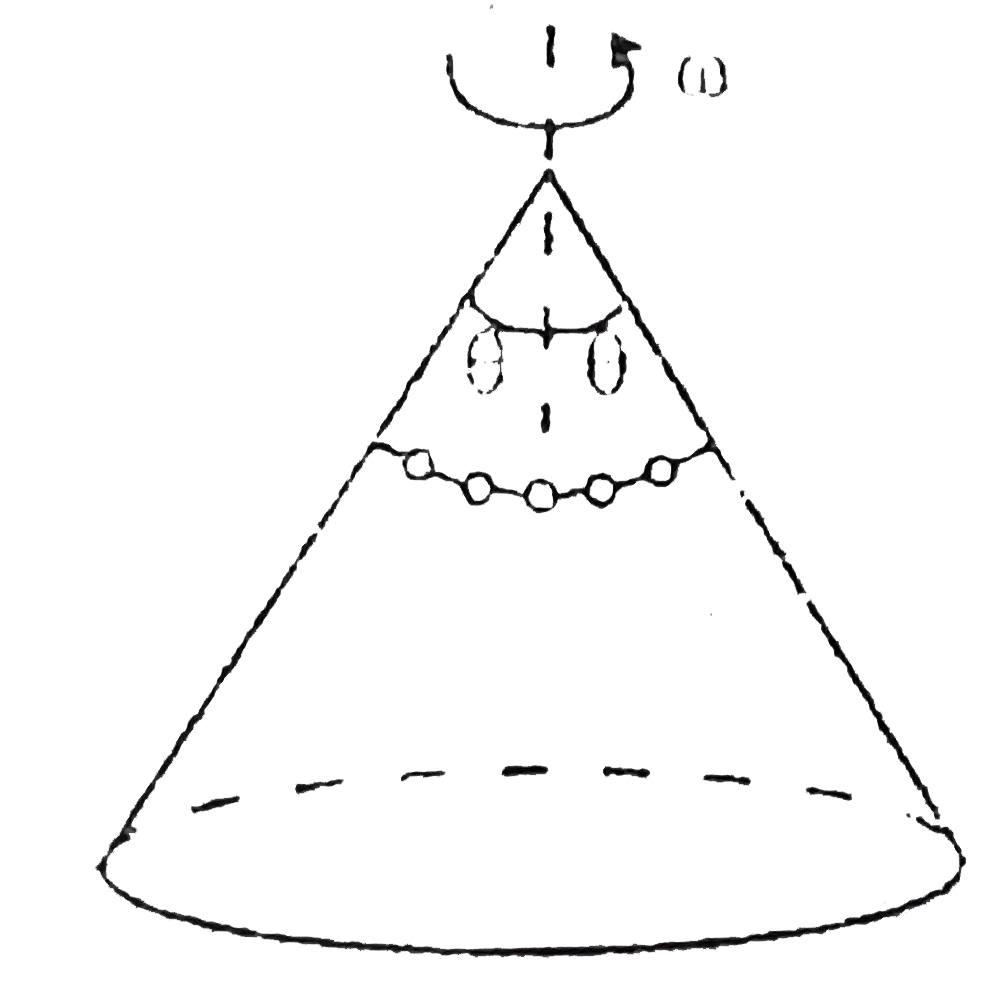
A chain of mass m forming a circle of radius R is slipped on a smooth round cone with half- angle $θ$ . Find the tension in the chain if it rotates with a constant angular velocity $ω$ about a vertical axis coinciding with the symmetry axis of the cone .

A

$(R ω^{2} + g cot θ) \frac{m}{2 π}$

B

$(R ω^{2} - g cot θ) \frac{m}{2 π}$

C

$(R ω^{2} + g cot θ) \frac{m}{π}$

D

$(R ω - g cot θ) \frac{m}{2 π}$

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:A

To find the tension in the chain that is rotating around a smooth cone, we can follow these steps:
Step 1: Understand the System
We have a chain of mass $m$ forming a circle of radius $R$ on a smooth cone with a half-angle $θ$ . The chain rotates with a constant angular velocity $ω$ about the vertical axis.
Step 2: Draw the Free Body Diagram (FBD)
Consider an infinitesimal mass element $d m$ of the chain. The forces acting on this mass element are:
- The weight $d m \cdot g$ acting downward.
- The tension $T$ acting along the chain.
- The normal force $d N$ acting perpendicular to the surface of the cone.
Step 3: Analyze Forces in Horizontal and Vertical Directions
1. Horizontal Forces: In the horizontal direction, the component of the tension providing the centripetal force is:
$2 T sin (θ) = d m \cdot ω^{2} \cdot R$
This can be named as Equation (1).
2. Vertical Forces: In the vertical direction, the weight of the mass element is balanced by the vertical component of the normal force:
$m g = d N \cdot cos (θ)$
This can be named as Equation (2).
Step 4: Relate Normal Force to Mass Element
From Equation (2), we can express the normal force $d N$ in terms of $m g$ :
$d N = \frac{m g}{cos (θ)}$
Step 5: Substitute Normal Force into Horizontal Forces Equation
Substituting $d N$ into Equation (1):
$2 T sin (θ) + \frac{m g}{cos (θ)} = d m \cdot ω^{2} \cdot R$
Step 6: Solve for Tension $T$
Rearranging the equation to isolate $T$ :
$T = \frac{d m \cdot ω^{2} \cdot R - \frac{m g}{cos (θ)}}{2 sin (θ)}$
Step 7: Integrate Over the Entire Chain
Since $d m = \frac{m}{2 π R} d θ$ (where $d θ$ is the infinitesimal angle subtended by the mass element), we can integrate over the full circle to find the total tension in the chain.
Final Expression for Tension
After integrating and simplifying, we find:
$T = \frac{R ω^{2} + g cot (θ)}{2 π}$
Conclusion
Thus, the tension in the chain is given by:
$T = \frac{R ω^{2} + g cot (θ)}{2 π}$

Updated on:7/8/2024

|

Class 12 PHYSICS JEE MOCK TEST 2

Similar Questions

Knowledge Check

A stone of mass M tied at the end of a string, is moving in a circular of radius R, with a constant angular velocity $ω$ . The work done on the stone, in any half circle I s
A $π M R^{2} ω^{2}$
B $2 M R^{2} ω^{2}$
C $M R^{2} ω^{2}$
Dzero

Recommended Questions

Home
Ask Doubt
Profile