One mole of a diatomic gas undergoes a thermodynamic process, whose process equation is P∝V2. The molar specific heat of the gas is
17R3
17R6
15R4
15R8
The correct Answer is:B
To find the molar specific heat of a diatomic gas undergoing a thermodynamic process described by the equation P∝V2, we can follow these steps:
Step 1: Understand the relationship
The given relationship P∝V2 implies that P=kV2 for some constant k. This suggests that we can express the relationship in terms of a polytropic process.
Step 2: Identify the polytropic process
In a polytropic process, the relationship can be expressed as:
PVn=constant
Comparing this with our equation P=kV2, we can rewrite it as:
PV−2=k
This indicates that n=−2.
Step 3: Use the formula for molar specific heat
The formula for the molar specific heat C in a polytropic process is given by:
C=Cv+R1−n
where Cv is the molar specific heat at constant volume, and R is the universal gas constant.
Step 4: Determine Cv for a diatomic gas
For a diatomic gas, the molar specific heat at constant volume Cv is:
Cv=5R2
Step 5: Substitute values into the specific heat formula
Now substituting Cv and n into the specific heat formula:
C=5R2+R1−(−2)
This simplifies to:
C=5R2+R1+2=5R2+R3
Step 6: Find a common denominator and combine the terms
To combine 5R2 and R3, we find a common denominator, which is 6:
C=15R6+2R6=17R6
Final Answer
Thus, the molar specific heat of the gas is:
C=17R6
The given relationship P∝V2 implies that P=kV2 for some constant k. This suggests that we can express the relationship in terms of a polytropic process.
In a polytropic process, the relationship can be expressed as:
PVn=constant
Comparing this with our equation P=kV2, we can rewrite it as:
PV−2=k
This indicates that n=−2.
The formula for the molar specific heat C in a polytropic process is given by:
C=Cv+R1−n
where Cv is the molar specific heat at constant volume, and R is the universal gas constant.
For a diatomic gas, the molar specific heat at constant volume Cv is:
Cv=5R2
Now substituting Cv and n into the specific heat formula:
C=5R2+R1−(−2)
This simplifies to:
C=5R2+R1+2=5R2+R3
To combine 5R2 and R3, we find a common denominator, which is 6:
C=15R6+2R6=17R6
Thus, the molar specific heat of the gas is:
C=17R6
Similar Questions
an ideal diatomic gas undergoes a polytropic process described by the equation P√V=constant . The molar heat capacity of the gas during this process is
View SolutionOne mole of an ideal monatomic gas undergoes a process described by the equation PV3= constant. The heat capacity of the gas during this process is
View SolutionTwo moles of an ideal mono-atomic gas undergoes a thermodynamic process in which the molar heat capacity 'C' of the gas depends on absolute temperature as C=RTT0, where R is gas consant and T0 is the initial temperature of the gas. (V0 is the initial of the gas). Then answer the following questions:
The equation of process is
View SolutionA certain amount of ideal monoatomic gas undergoes a process given by TV1/2= constant. The molar specific heat of the gas for the process will be given by
View SolutionOne mole of an ideal monatomic gas undergoes the process P=αT1/2, where α is constant . If molar heat capacity of the gas is βR1 when R = gas constant then find the value of β.
View SolutionAn ideal diatomic gas undergoes a thermodynamic process as shown in the P−V diagram. The process AB is isochoric while the process BC is isothermal. The total heat gein to the gas in the process is nearly (use ln2=0.7)
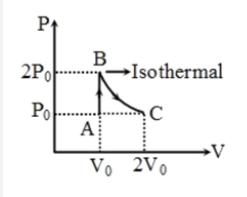
View SolutionA monatomic gas undergoes a thermodynamic process such that T∝V−27 (T = temperature and V = volume of the gas) As heat is supplied to the gas, choose INCORRECT option.
View SolutionA certain amount of an ideal monoatomic gas undergoes a thermodynamic process such that VT2= constat where V= volume of gas, T= temperature of gas. Then under process
View SolutionOne mole of an ideal gas undergoes a process such that P∝1T. The molar heat capacity of this process is 4R.
View SolutionOne mole of a monoatomic ideal gas undergoes the process A→B in the given P-V diagram. What is the specific heat for this process?
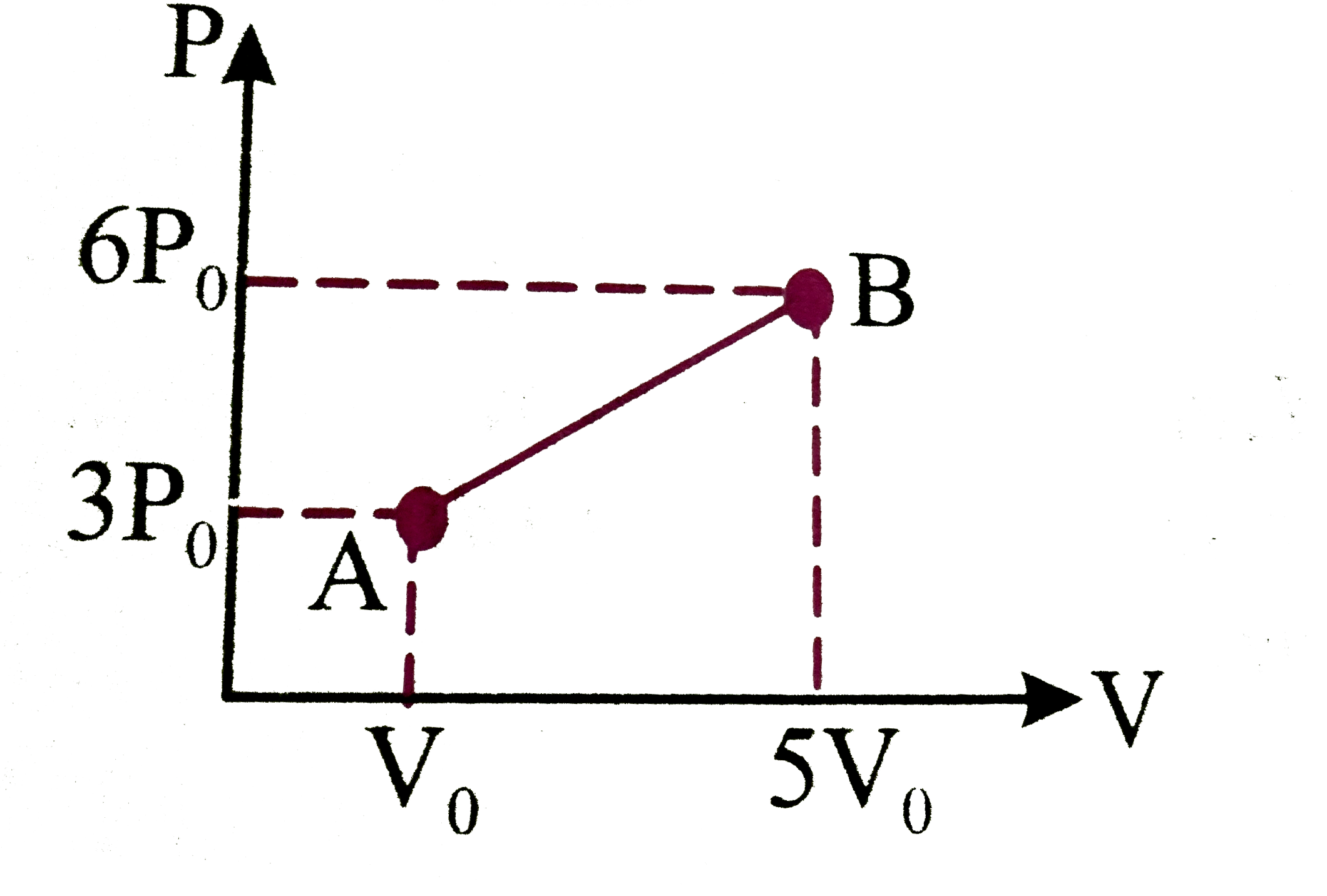
View Solution
