Two coplanar concentric circular coils of radii r and 2r, have the same number of turns n. The smaller coil carries a clockwise current i, while the larger coil carries an anticlockwise current 2i. The magnetic field induction at the centre is
3μ0ni4r
zero
μ0ni4r
μ0ni2r
The correct Answer is:B
To find the magnetic field induction at the center of two coplanar concentric circular coils with given parameters, we can follow these steps:
1. Identify the Parameters:
- Smaller coil (Coil 1) has radius r and carries a clockwise current i.
- Larger coil (Coil 2) has radius 2r and carries an anticlockwise current 2i.
- Both coils have the same number of turns n.
2. Magnetic Field Due to Coil 1:
- The formula for the magnetic field B at the center of a circular coil is given by:
B=μ0nI2R
- For Coil 1 (smaller coil):
B1=μ0ni2r
- Since the current is clockwise, the direction of the magnetic field B1 is directed downwards (into the plane).
3. Magnetic Field Due to Coil 2:
- For Coil 2 (larger coil):
B2=μ0n(2i)2(2r)=μ0ni2r
- Since the current is anticlockwise, the direction of the magnetic field B2 is directed upwards (out of the plane).
4. Combine the Magnetic Fields:
- The magnetic fields B1 and B2 act in opposite directions:
- B1 (downwards) = μ0ni2r
- B2 (upwards) = μ0ni2r
- Therefore, the net magnetic field Bnet at the center is:
Bnet=B2−B1=μ0ni2r−μ0ni2r=0
5. Conclusion:
- The magnetic field induction at the center of the coils is zero.
Final Answer:
The magnetic field induction at the center is 0.
---
- Smaller coil (Coil 1) has radius r and carries a clockwise current i.
- Larger coil (Coil 2) has radius 2r and carries an anticlockwise current 2i.
- Both coils have the same number of turns n.
- The formula for the magnetic field B at the center of a circular coil is given by:
B=μ0nI2R
- For Coil 1 (smaller coil):
B1=μ0ni2r
- Since the current is clockwise, the direction of the magnetic field B1 is directed downwards (into the plane).
- For Coil 2 (larger coil):
B2=μ0n(2i)2(2r)=μ0ni2r
- Since the current is anticlockwise, the direction of the magnetic field B2 is directed upwards (out of the plane).
- The magnetic fields B1 and B2 act in opposite directions:
- B1 (downwards) = μ0ni2r
- B2 (upwards) = μ0ni2r
- Therefore, the net magnetic field Bnet at the center is:
Bnet=B2−B1=μ0ni2r−μ0ni2r=0
- The magnetic field induction at the center of the coils is zero.
The magnetic field induction at the center is 0.
Similar Questions
Knowledge Check
The magnetic moment of a current I carrying circular coil of radius r and number of turns N varies as
A1r2B1rCrDr2A circular coil of radius 10 cm having 100 turns carries a current of 3.2 A. The magnetic field at the center of the coil is
A2.01×10−3TB5.64×10−3TC2.64×10−3TD5.64×10−3T
A circular coil of 200 mm diameter is made of 100 turns of thin wire and carries a current of 50 mA. Find the magnetic field induction at the centre of the coil.
View SolutionTwo concentric coplanar circular loops of radii r1 and r2 carry currents of respectively i1 and i2 in opposite direction (one clockwise and the other anticlockwise). The magnetic induction at the centre of the loops is half that due to i1 alone at the centre. if r2=2r1. the value of i2/i1 is
View SolutionA coil having N turns carry a current I as shown in the figure. The magnetic field intensity at point P is
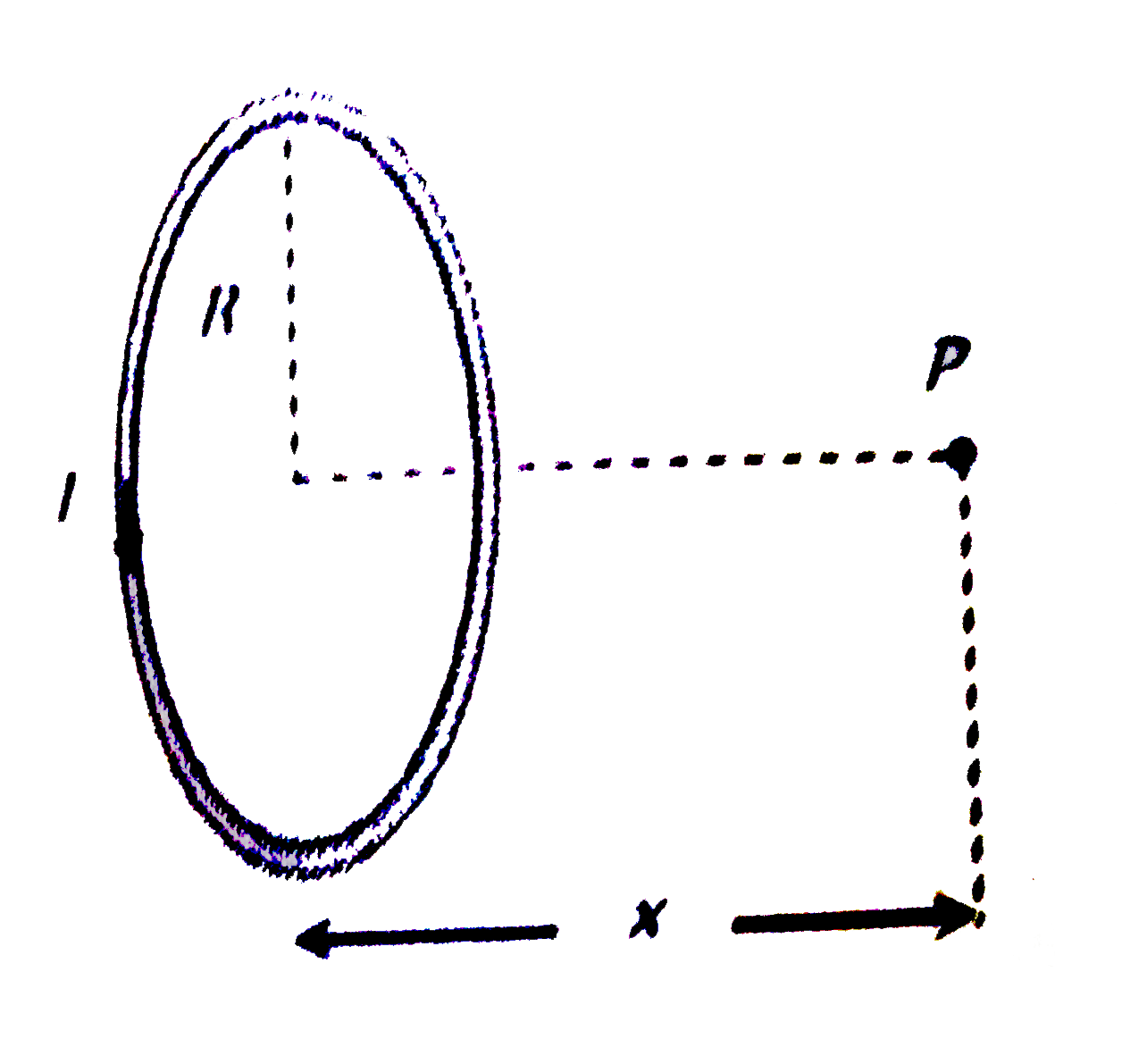
View SolutionTwo circular coils mounted parallel to each other on the same axis carry steady currents. If an observer between the coils reports. that one coil is carrying a clockwise current i1 While the other is carrying a counter - clockwise current i2 then the two coils experience
View SolutionA moving coil galvanometer has N numbr of turns in a coil of effective area A, it carries a current I. The magnetic field B is radial. The torque acting on the coil is
View SolutionAt the centre of a fixed large circular coil of radius R a much smaller circular coil of radius r is placed .The two coils are concentric and are in the same plane .The larger coil carries a current I The smaller coil is set to rotate with a constant angular velocity ω about an axis along their common diameter .Calculate the emf induced in the smaller coil after a time t of its start of ratation
View Solution