A 10 kg stone is suspended with a rope of breaking strength 30 kg-wt. The minimum time in which the stone can be raised through a height 10 m starting from rest is (Take, g=10Nkg−1).
0.5s
1.0s
√23s
2.0s
The correct Answer is:B
To solve the problem, we need to determine the minimum time required to raise a 10 kg stone through a height of 10 meters, given that the rope has a breaking strength of 30 kg-wt. We will follow these steps:
Step 1: Calculate the Maximum Force
The breaking strength of the rope is given as 30 kg-wt. We can convert this to Newtons using the acceleration due to gravity (g = 10 N/kg).
Breaking Strength=30kg-wt=30×g=30×10N=300N
Step 2: Calculate the Maximum Acceleration
The maximum force that can be applied is 300 N. The mass of the stone is 10 kg. We can use Newton's second law to find the maximum acceleration (a_max) that can be applied to the stone.
F=m⋅a⟹amax=Fm=300N10kg=30m/s2
Step 3: Account for Gravitational Acceleration
The stone is also subject to the acceleration due to gravity, which acts downward. Therefore, the effective acceleration (a_eff) with which we can raise the stone is given by:
aeff=amax−g=30m/s2−10m/s2=20m/s2
Step 4: Use the Equation of Motion
We will use the equation of motion to find the time (t) it takes to raise the stone through a height (s) of 10 meters. The equation is:
s=ut+12at2
Since the stone starts from rest, the initial velocity (u) is 0. Thus, the equation simplifies to:
s=12aefft2
Substituting the values we have:
10m=12⋅20m/s2⋅t2
Step 5: Solve for Time
Now we can solve for t:
10=10t2⟹t2=1⟹t=√1=1s
Final Answer
The minimum time in which the stone can be raised through a height of 10 meters is 1 second.
---
The breaking strength of the rope is given as 30 kg-wt. We can convert this to Newtons using the acceleration due to gravity (g = 10 N/kg).
The maximum force that can be applied is 300 N. The mass of the stone is 10 kg. We can use Newton's second law to find the maximum acceleration (a_max) that can be applied to the stone.
The stone is also subject to the acceleration due to gravity, which acts downward. Therefore, the effective acceleration (a_eff) with which we can raise the stone is given by:
We will use the equation of motion to find the time (t) it takes to raise the stone through a height (s) of 10 meters. The equation is:
Now we can solve for t:
The minimum time in which the stone can be raised through a height of 10 meters is 1 second.
Similar Questions
A 10 kg wt is suspended as shown below then tension T1 & T2 are
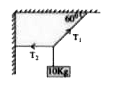
View SolutionA 24 kg block resting on a floor has a rope tied to its top. The maximum tension , the rope can withstand without breaking is 310 N . The minimum time in which the block can be lifted a vertical distance of 4.6 m by pulling on the rope is
View Solution
Knowledge Check
A crane lifts a mass of 100 kg to a height of 10 m in 20 s. The power of the crane is (Take g=10ms−2)
A100 WB200 WC250 WD500 WA stone of mass 5 kg is tied to a string of length 10 m is whirled round in a horizontal circle. What is the maximum speed with which the stone can be whirled around if the string can withstand a maximum tension of 200 N?
A10ms−1B15ms−1C20ms−1D25ms−1
A monkey of 25 kg is holding a vertical rope. The rope does not break if a body of mass less than 30 kg is suspended with the rope. What will be the maximum acceleration with which the monkey can climb up along the rope ? (Take g=10ms−2)
View SolutionA body of mass 50 kg and specific gravity force is to be lifted using a rope of breaking strength of 60 kg wt. The acceleration with which it can be pulled up in least interval of time
View SolutionA body of mass 60 kg is holding a vertical rope . The rope can break when a mass of 75 kg is suspended from it. The maximum acceleration with which the boy can climb the rope without breaking it is :(g=10m/s2)
View SolutionA stone is projected vertically up from the ground with velocity 40ms−1 . The interval of time between the two instants at which the stone is at a height of 60 m above the ground is (g=10ms−2)
View SolutionA string tied on a roof can bear a maximum tension of 50 kg wt. The minimum acceleration that can be acquired by a man of 98 kg to descend will be [take g = 9⋅8ms2]
View SolutionA stone is projected in air. Its time of flight is 3s and range is 150m. Maximum height reached by the stone is (Take, g=10ms−2)
View Solution
