A monkey of 25 kg is holding a vertical rope. The rope does not break if a body of mass less than 30 kg is suspended with the rope. What will be the maximum acceleration with which the monkey can climb up along the rope ? (Take g=10ms−2)
2ms−2
2.5ms−2
3ms−2
4ms−2
The correct Answer is:A
To solve the problem step by step, we can follow these instructions:
Step 1: Understand the forces acting on the monkey
The monkey has a mass of 25 kg and is climbing up a rope. The forces acting on the monkey are:
- The gravitational force acting downwards, which is Wm=mm⋅g
- The tension in the rope acting upwards, which we will denote as T
Step 2: Calculate the gravitational force on the monkey
Using the given value of g=10m/s2:
Wm=mm⋅g=25kg⋅10m/s2=250N
Step 3: Determine the maximum tension in the rope
The problem states that the rope can support a mass of less than 30 kg. Therefore, the maximum tension Tmax in the rope is:
Tmax=mmax⋅g=30kg⋅10m/s2=300N
Step 4: Write the equation of motion for the monkey
When the monkey climbs up with an acceleration A, the net force acting on the monkey can be expressed as:
T−Wm=mm⋅A
Substituting the values we have:
T−250N=25kg⋅A
Step 5: Substitute the maximum tension into the equation
To find the maximum acceleration, we will use the maximum tension:
300N−250N=25kg⋅A
This simplifies to:
50N=25kg⋅A
Step 6: Solve for acceleration A
Now, we can solve for A:
A=50N25kg=2m/s2
Conclusion
The maximum acceleration with which the monkey can climb up along the rope is:
2m/s2
The monkey has a mass of 25 kg and is climbing up a rope. The forces acting on the monkey are:
- The gravitational force acting downwards, which is Wm=mm⋅g
- The tension in the rope acting upwards, which we will denote as T
Using the given value of g=10m/s2:
Wm=mm⋅g=25kg⋅10m/s2=250N
The problem states that the rope can support a mass of less than 30 kg. Therefore, the maximum tension Tmax in the rope is:
Tmax=mmax⋅g=30kg⋅10m/s2=300N
When the monkey climbs up with an acceleration A, the net force acting on the monkey can be expressed as:
T−Wm=mm⋅A
Substituting the values we have:
T−250N=25kg⋅A
To find the maximum acceleration, we will use the maximum tension:
300N−250N=25kg⋅A
This simplifies to:
50N=25kg⋅A
Now, we can solve for A:
A=50N25kg=2m/s2
The maximum acceleration with which the monkey can climb up along the rope is:
2m/s2
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Match the columns
7 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
A monkey of mass 20kg is holding a vertical rope. The rope will not break when a mass of 25kg is suspended from it but will break it the mass exeeds 25kg . What is the maximum acceleration with which the monkey can climb up along the rope? (g=10m/s2) .
View SolutionA monkey of mass 20kg is holding a vertical rope. The rope will not break when a mass of 25kg is suspended from it but will break it the mass exeeds 25kg . What is the maximum acceleration with which the monkey can climb up along the rope? (g=10m/s2) .
View Solution
Knowledge Check
A monkey of mass 40 kg climbs on a massless rope which can stand a maximum tension of 500 N. In which of the following cases will the rope break? (Take g=10ms−2)
 AThe monkey climbs up with an acceleration of 5ms−2.BThe monkey climbs down with an acceleration of 5ms−2.CThe monkey climbs up with a uniform speed 5ms−2.DThe monkey falls down, the rope freely under gravity.
AThe monkey climbs up with an acceleration of 5ms−2.BThe monkey climbs down with an acceleration of 5ms−2.CThe monkey climbs up with a uniform speed 5ms−2.DThe monkey falls down, the rope freely under gravity.
A body of mass 60 kg is holding a vertical rope . The rope can break when a mass of 75 kg is suspended from it. The maximum acceleration with which the boy can climb the rope without breaking it is :(g=10m/s2)
View SolutionA money of mass 40 kg climbs up a rope, of breaking load 600 N hanging from a ceiling. If it climbs up the rope with the maximum possible acceleration, then the time taken by monkey to climb up is [length of rope is 10 m]
View SolutionA rope of negligible mass passes over a pulley of negligible mass attached to the ceiling, as shown in figure. One end of the rope is held by Student A of mass 70kg, who is at rest on the floor. The opposite end of the rope is held by Student B of mass 60kg, who is suspended at rest above the floor. The minimum acceleration a0 with which the Student B should climb up the rope to lift the Student A upward off the floor. (g=10m/s2)
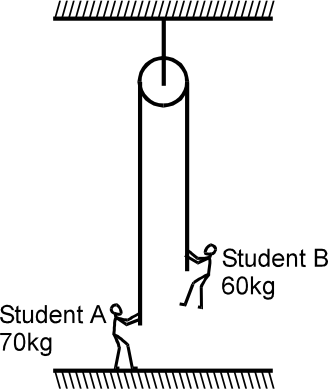
View SolutionA rope of negligible mass passes over a pulley of negligible mass attached to the ceiling, as shown in figure. One end of the rope is held by Student A of mass 70kg, who is at rest on the floor. The opposite end of the rope is held by Student B of mass 60kg, who is suspended at rest above the floor. The minimum acceleration a0 with which the Student B should climb up the rope to lift the Student A upward off the floor. (g=10m/s2)

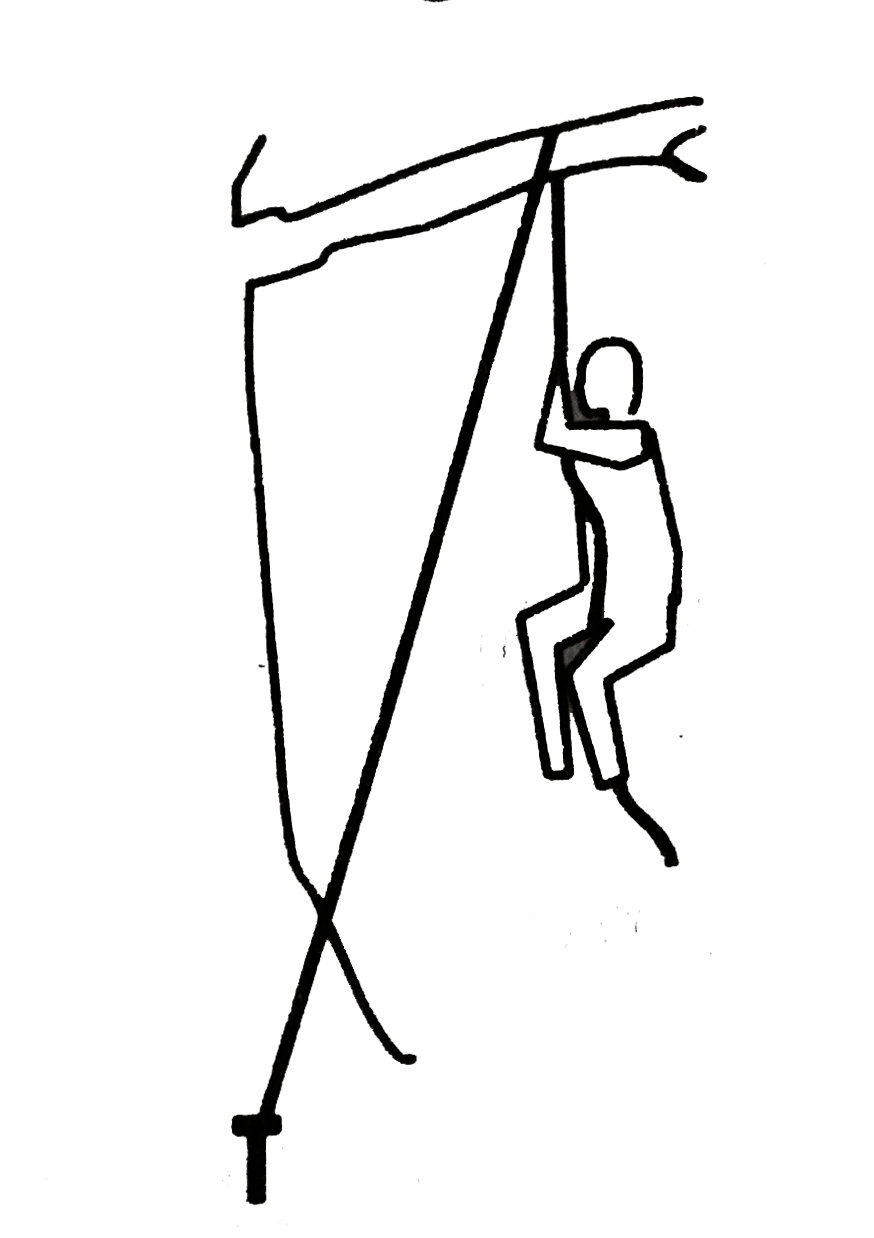
View SolutionA light rope fixed at one end of a wooden clamp on the ground passes over a tree branch and hangs on the other side. It makes an angle of 300 with the ground. A man weighing (60 kg) wants to climb up the rope. The wooden clamp can come out of the ground if an upward force greater than 360 N is applied it. Find the maximum acceleration in the upward direction with which the man can climb safely. Neglect friction at the tree branch. Take g=10ms2
View SolutionThe maximum tension a rope can withstand is 60 kg.wt. The ratio of maximum acceleration with which two boys of masses 20 kg and 30 kg can climb up the rope at the same time is
View SolutionAs shown in figure a monkey of 20g mass is holding a light rope that passes over a frictionless pulley. A bunch of bananas of the same mass is tied to the other end of rope. Inorder to get access to the bunch the monkey starts climbing the rope. The distance between the monkey and the bananas is

View Solution
