For an infinitely long solid cylinder of radius R having a uniform density , the gravitational field at a distance r1 is E1 and at a distance r2 is E2 , then
E1<E2 for r1<r2<R
E1>E2 for R<r1<r2
both 1 and 2
none of the above
The correct Answer is:C
To solve the problem regarding the gravitational field due to an infinitely long solid cylinder, we need to analyze the gravitational field at different distances from the center of the cylinder.
1. Understanding the Gravitational Field: The gravitational field E due to an infinitely long solid cylinder varies depending on the distance from the axis of the cylinder. The gravitational field inside the cylinder (for r<R) and outside the cylinder (for r>R) behaves differently.
2. Gravitational Field Inside the Cylinder: For a point inside the cylinder (where r<R), the gravitational field E is given by:
E=GM(r)r2
where M(r) is the mass enclosed within radius r. Since the mass is uniformly distributed, M(r) can be calculated based on the volume of the cylinder up to radius r.
3. Gravitational Field Outside the Cylinder: For a point outside the cylinder (where r>R), the gravitational field E behaves as if all the mass of the cylinder were concentrated at its axis. Thus, it is given by:
E=GMr2
where M is the total mass of the cylinder.
4. Comparing E1 and E2:
- Case A: If r1<r2<R (both points are inside the cylinder):
- Since E increases as we move closer to the surface of the cylinder, we have E1<E2. Thus, this statement is correct.
- Case B: If r1>R and r1<r2 (both points are outside the cylinder):
- Here, E decreases as we move away from the cylinder. Therefore, E1>E2 for r1<r2. This statement is also correct.
5. Conclusion: Both statements regarding the gravitational fields E1 and E2 are correct. Therefore, the final answer is that both options A and B are correct.
Final Answer:
Both options A and B are correct.
E=GM(r)r2
where M(r) is the mass enclosed within radius r. Since the mass is uniformly distributed, M(r) can be calculated based on the volume of the cylinder up to radius r.
E=GMr2
where M is the total mass of the cylinder.
- Case A: If r1<r2<R (both points are inside the cylinder):
- Since E increases as we move closer to the surface of the cylinder, we have E1<E2. Thus, this statement is correct.
- Case B: If r1>R and r1<r2 (both points are outside the cylinder):
- Here, E decreases as we move away from the cylinder. Therefore, E1>E2 for r1<r2. This statement is also correct.
Both options A and B are correct.
Similar Questions
An infinitely long solid cylinder of radius R has a uniform volume charge density ρ. It has a spherical cavity of radius R/2 with its centre on the axis of cylinder, as shown in the figure. The magnitude of the electric field at the point P, which is at a distance 2R form the axis of the cylinder, is given by the expression 23rR16ke0 . The value of k is .
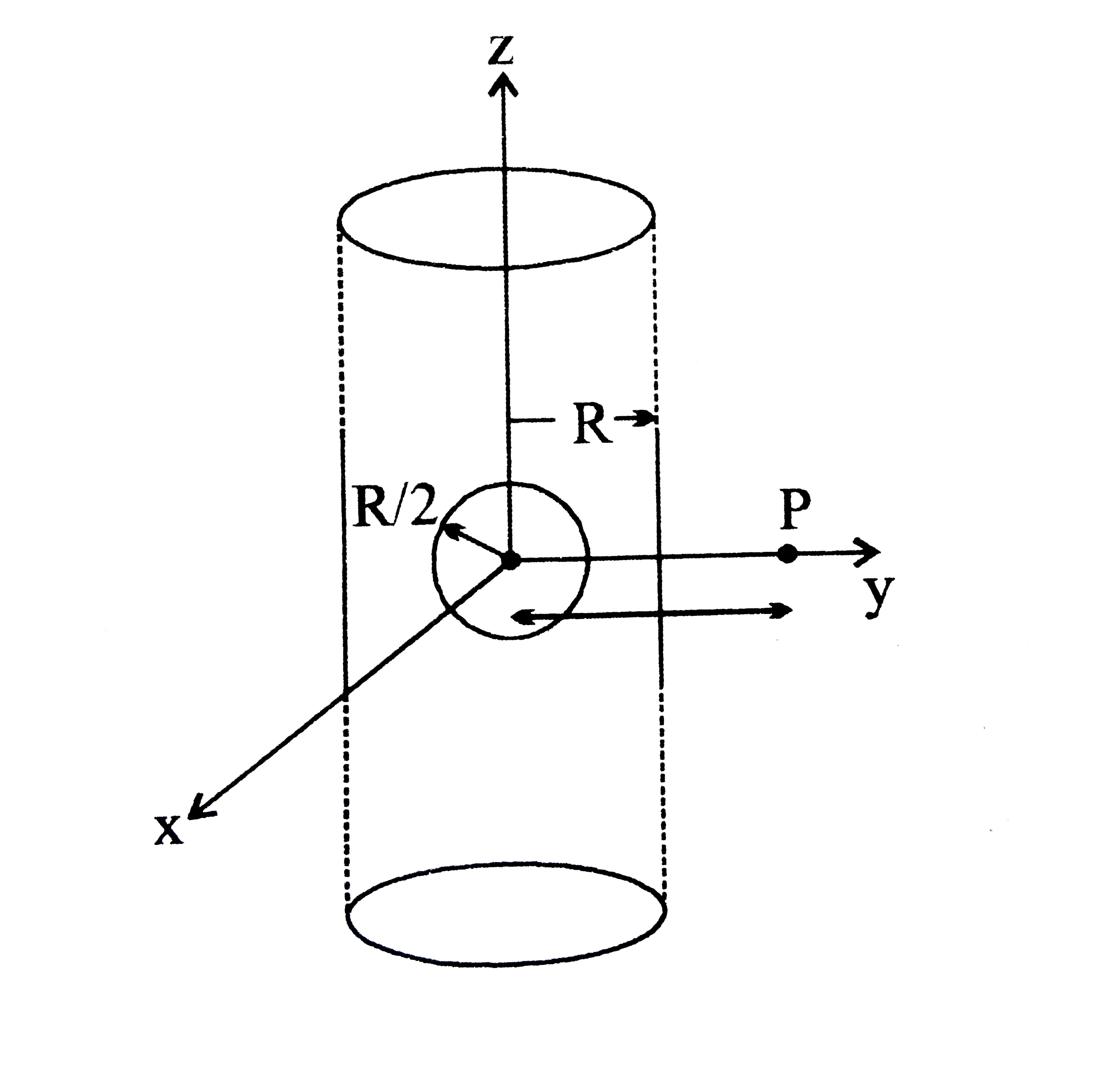 .
.
View SolutionInside a uniformly charged infinitely long cylinder of radius 'R' and volume charge density 'rho' there is a spherical cavity of radius 'R//2'. A point 'P' is located at a dsintance 2R from the axis of the cylinder as shown. Then the electric field strength at the point 'P' is
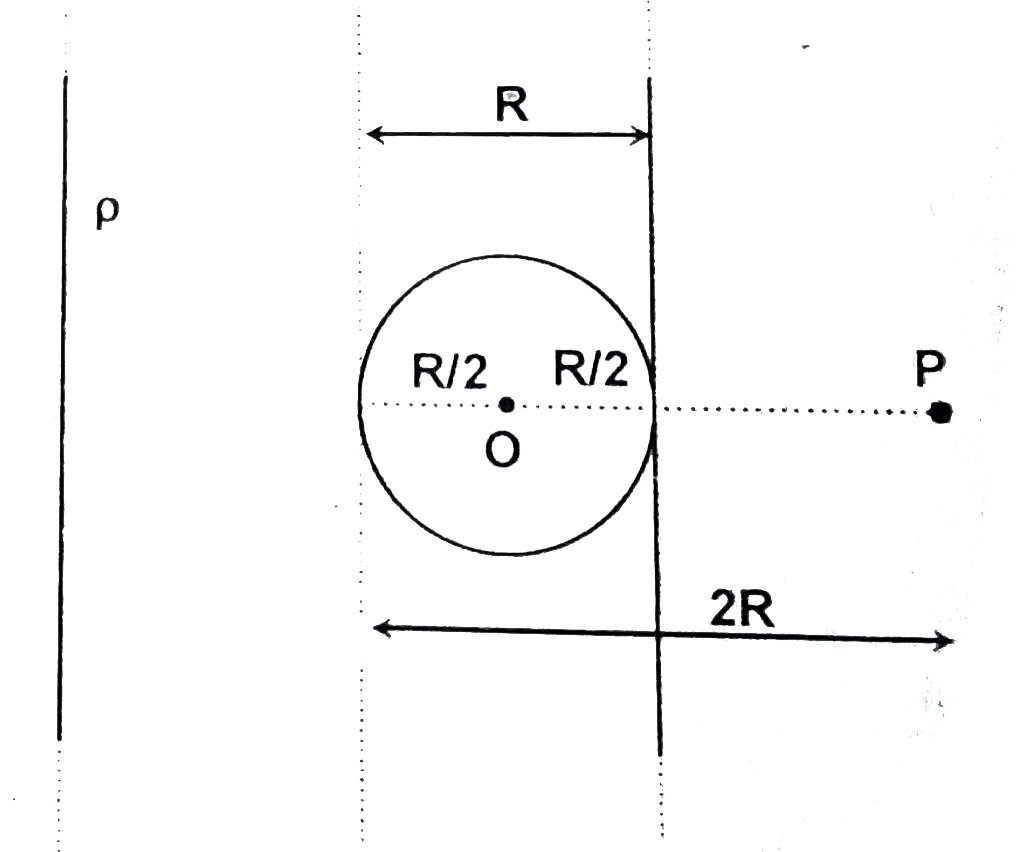
View Solution
Knowledge Check
An infinite cylinder of radius ro, carrying linear charge density λ. The equation of the equipotential surface for the cylinder is
Ar=r0eπε0[V(r)+V(r0)]λBr=r0e2πε0[V(r)−V(r0)]λ2Cr=r0e−2πε0[V(r)=V(r0)]λDr=r0e−2πε0[V(r)−V(r0)]λThere is a solid sphere of radius R having uniformly distributed charge throughout it. What is the relation between electric field E and distance r from the centre (r is less than R) ?
AE∝r−2BE∝r−1CE∝rDE∝r2
An infinitely long cylinderical wire of radius R is carrying a current with current density j=αr3 (where α is constant and r is the distance from the axis of the wire). If the magnetic fixed at r=R2 is B1 and at r=2R is B2 then the ratio B2B1 is
View SolutionA non-conducting solid sphere of radius R, has a uniform charge density. The graph representing variation of magnitude of electric field (E) as a function of distance (x) from the centre of the sphere is
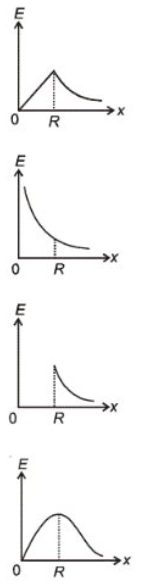
View SolutionThe gravitational potential at a point outside the solid sphere of radius "R" and at a distance of "r" will be :
View SolutionA solid non-conduction cylinder of radius R is charge such that volume charge density is proporation to r where r is distance from axis. The electric field E at a distance r(r<R) well depend on r as.
View SolutionThe distance between the centres of the Moon and the earth is D. The mass of the earth is 81 times the mass of the Moon. At what distance from the centre of the earth, the gravitational force will be zero?
View SolutionA current l is flowing through a long straight solid conductor of radius R = 4 cm. Magnetic field at a distance 2 cm from the axis of conductor is B0 The distance from the axis, where magnetic field is 1.5 B0 is (current density is uniform)
View Solution
