In a photoelectric effect experiment, stopping potential changes by 30 volt if we change frequency of the radiation. Then the magnitude of change in the frequency is : (h=6×10−34J−s)
4×10−15s−1
8×1015s−1
1016s−1
18×1015s−1
The correct Answer is:B
To solve the problem, we need to analyze the relationship between the stopping potential and the frequency of the incident radiation in the photoelectric effect.
1. Understanding the Photoelectric Effect:
The stopping potential V0 in a photoelectric effect experiment is related to the frequency of the incident light by the equation:
eV0=hν−ϕ
where e is the charge of an electron, h is Planck's constant, ν is the frequency of the incident radiation, and ϕ is the work function of the material.
2. Change in Stopping Potential:
According to the problem, the stopping potential changes by ΔV0=30 volts. This means:
eΔV0=hΔν
where Δν is the change in frequency.
3. Rearranging the Equation:
Rearranging the equation gives us:
Δν=eΔV0h
4. Substituting Known Values:
We know:
- e=1.6×10−19 C (charge of an electron)
- h=6×10−34 J·s (Planck's constant)
- ΔV0=30 V
Substituting these values into the equation:
Δν=(1.6×10−19C)(30V)6×10−34J⋅s
5. Calculating the Change in Frequency:
Δν=4.8×10−186×10−34=8×1015Hz
6. Final Answer:
The magnitude of the change in frequency is:
Δν=8×1015Hz
Conclusion:
Thus, the answer to the question is 8×1015Hz.
---
The stopping potential V0 in a photoelectric effect experiment is related to the frequency of the incident light by the equation:
eV0=hν−ϕ
where e is the charge of an electron, h is Planck's constant, ν is the frequency of the incident radiation, and ϕ is the work function of the material.
According to the problem, the stopping potential changes by ΔV0=30 volts. This means:
eΔV0=hΔν
where Δν is the change in frequency.
Rearranging the equation gives us:
Δν=eΔV0h
We know:
- e=1.6×10−19 C (charge of an electron)
- h=6×10−34 J·s (Planck's constant)
- ΔV0=30 V
Δν=(1.6×10−19C)(30V)6×10−34J⋅s
Δν=4.8×10−186×10−34=8×1015Hz
The magnitude of the change in frequency is:
Δν=8×1015Hz
Thus, the answer to the question is 8×1015Hz.
Similar Questions
Knowledge Check
In photoelectric effect experiment, the slope of the graph of the stopping potential versus frequency gives the value of :
AheBhCehDhce
In a photoelectric experiment the wavelength of incident light changes from 4000 Å to 2000 Å. The change in stopping potential is
View Solution(i) Plot a labelled graph of |Vs| where Vs is stopping potential versus frequency f of the incident radiation.
(ii) State how will you use this graph to determine the value of Planck.s constant.
View SolutionIn a photoelectric effect measurement, the stopping potential for a given metal is found to be V0 volt, when radiation of wavelength λ0 is used. If radiation of wavelength 2λ0 is used with the same metal, then the stopping potential (in V) will be
View SolutionIn a photoelectric effect experiment, the graph of stopping potential V versus reciprocal of wavelength obtained is shown in the figure. As the intensity of incident radiation is increased :

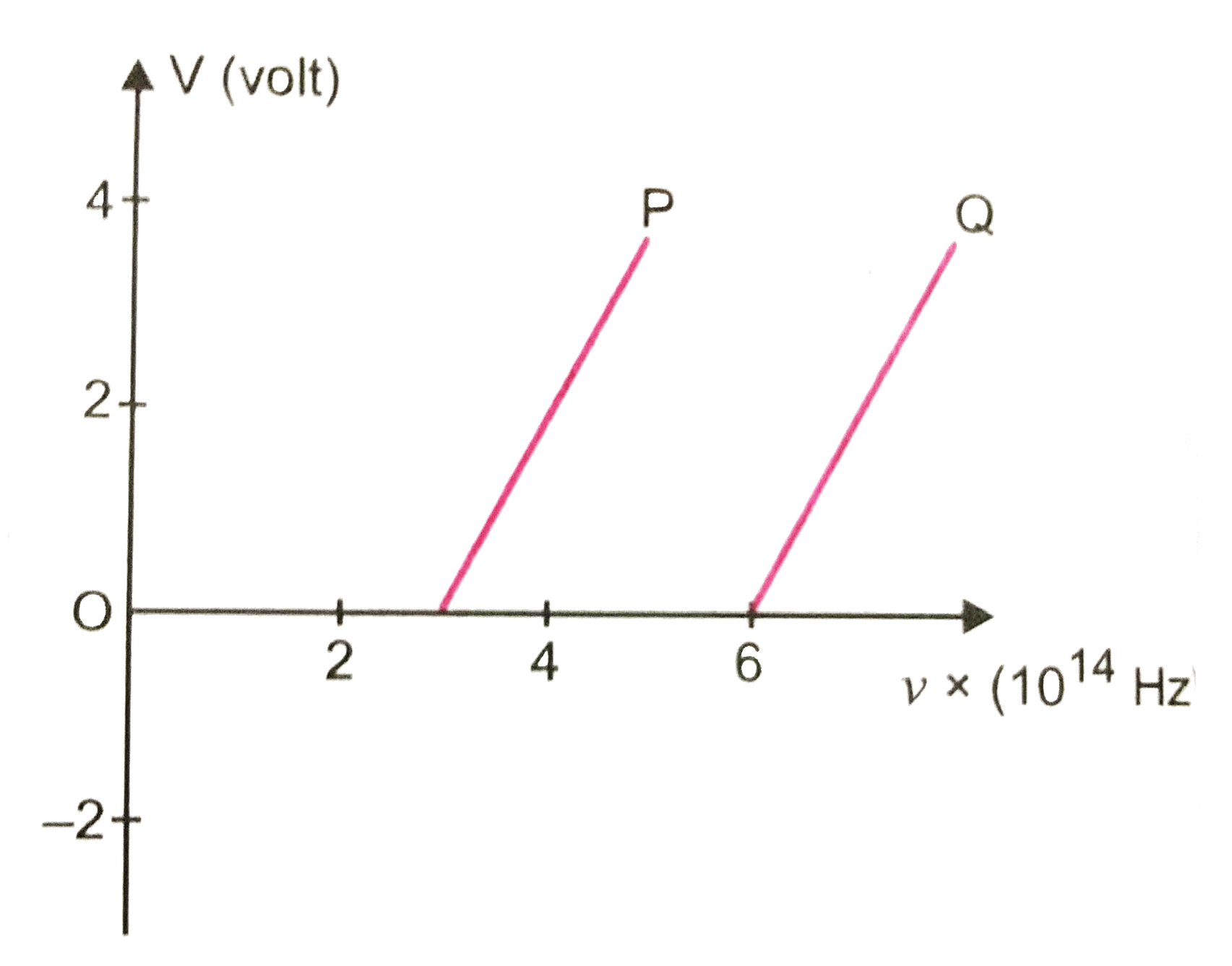
View SolutionIn the study of a photoelectric effect the graph between the stopping potential V and frequency ν of the incident radiation on two different metals P and Q is shown in fig.
(i) which one of two metals have higher threshold frequency
(ii) Determine the work function of the metal which has greater value
(iii) Find the maximum kinetic energy of electron emitted by light of frequency 8×1014Hz for this metal.
View SolutionThe change in frequency due to Doppler effect does not depend on
View SolutionCalculate the frequency of a photon, having energy 41.25 eV. (h=6.6×10−34Js).
View Solution

