In a photoelectric experiment the wavelength of incident light changes from 4000 Å to 2000 Å. The change in stopping potential is
6.2 V
3.1 V
2.1 V
4.1 V
To solve the problem of finding the change in stopping potential when the wavelength of incident light changes from 4000 Å to 2000 Å in a photoelectric experiment, we can follow these steps:
1. Understand the relationship between energy and wavelength:
The energy of a photon is given by the equation:
E=hcλ
where E is the energy of the photon, h is Planck's constant, c is the speed of light, and λ is the wavelength.
2. Set up the equations for both wavelengths:
For the first wavelength (λ1=4000Å):
E1=hcλ1=ϕ+eV1
For the second wavelength (λ2=2000Å):
E2=hcλ2=ϕ+eV2
3. Subtract the two equations:
By subtracting the second equation from the first, we eliminate the work function (ϕ):
hcλ1−hcλ2=eV1−eV2
This simplifies to:
hcλ1−hcλ2=e(V1−V2)
4. Factor out common terms:
hc(1λ1−1λ2)=e(V1−V2)
5. Express the change in stopping potential:
Rearranging gives:
V1−V2=hce(1λ1−1λ2)
The change in stopping potential (ΔV) is:
ΔV=V1−V2
6. Substitute known values:
- Convert wavelengths from Ångströms to meters:
λ1=4000Å=4000×10−10m,λ2=2000Å=2000×10−10m
- Substitute h=6.626×10−34Js, c=3×108m/s, and e=1.6×10−19C:
ΔV=(6.626×10−34Js)(3×108m/s)1.6×10−19C(14000×10−10−12000×10−10)
7. Calculate the values:
- Calculate 14000×10−10−12000×10−10:
14000×10−10=2.5×106,12000×10−10=5×106
ΔV=(6.626×10−34)(3×108)1.6×10−19×(−2.5×106)
8. Final calculation:
After calculating the above expression, we find:
ΔV≈3.1V
Final Answer:
The change in stopping potential is approximately 3.1 V.
The energy of a photon is given by the equation:
E=hcλ
where E is the energy of the photon, h is Planck's constant, c is the speed of light, and λ is the wavelength.
For the first wavelength (λ1=4000Å):
E1=hcλ1=ϕ+eV1
For the second wavelength (λ2=2000Å):
E2=hcλ2=ϕ+eV2
By subtracting the second equation from the first, we eliminate the work function (ϕ):
hcλ1−hcλ2=eV1−eV2
This simplifies to:
hcλ1−hcλ2=e(V1−V2)
hc(1λ1−1λ2)=e(V1−V2)
Rearranging gives:
V1−V2=hce(1λ1−1λ2)
The change in stopping potential (ΔV) is:
ΔV=V1−V2
- Convert wavelengths from Ångströms to meters:
λ1=4000Å=4000×10−10m,λ2=2000Å=2000×10−10m
- Substitute h=6.626×10−34Js, c=3×108m/s, and e=1.6×10−19C:
ΔV=(6.626×10−34Js)(3×108m/s)1.6×10−19C(14000×10−10−12000×10−10)
- Calculate 14000×10−10−12000×10−10:
14000×10−10=2.5×106,12000×10−10=5×106
ΔV=(6.626×10−34)(3×108)1.6×10−19×(−2.5×106)
After calculating the above expression, we find:
ΔV≈3.1V
The change in stopping potential is approximately 3.1 V.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In a photoelectric experiment, the graph of frequency v of incident light (in Hz) and stopping potential V (in V) is as shown in the figure. Planck's constant is (e is the elementary charge)
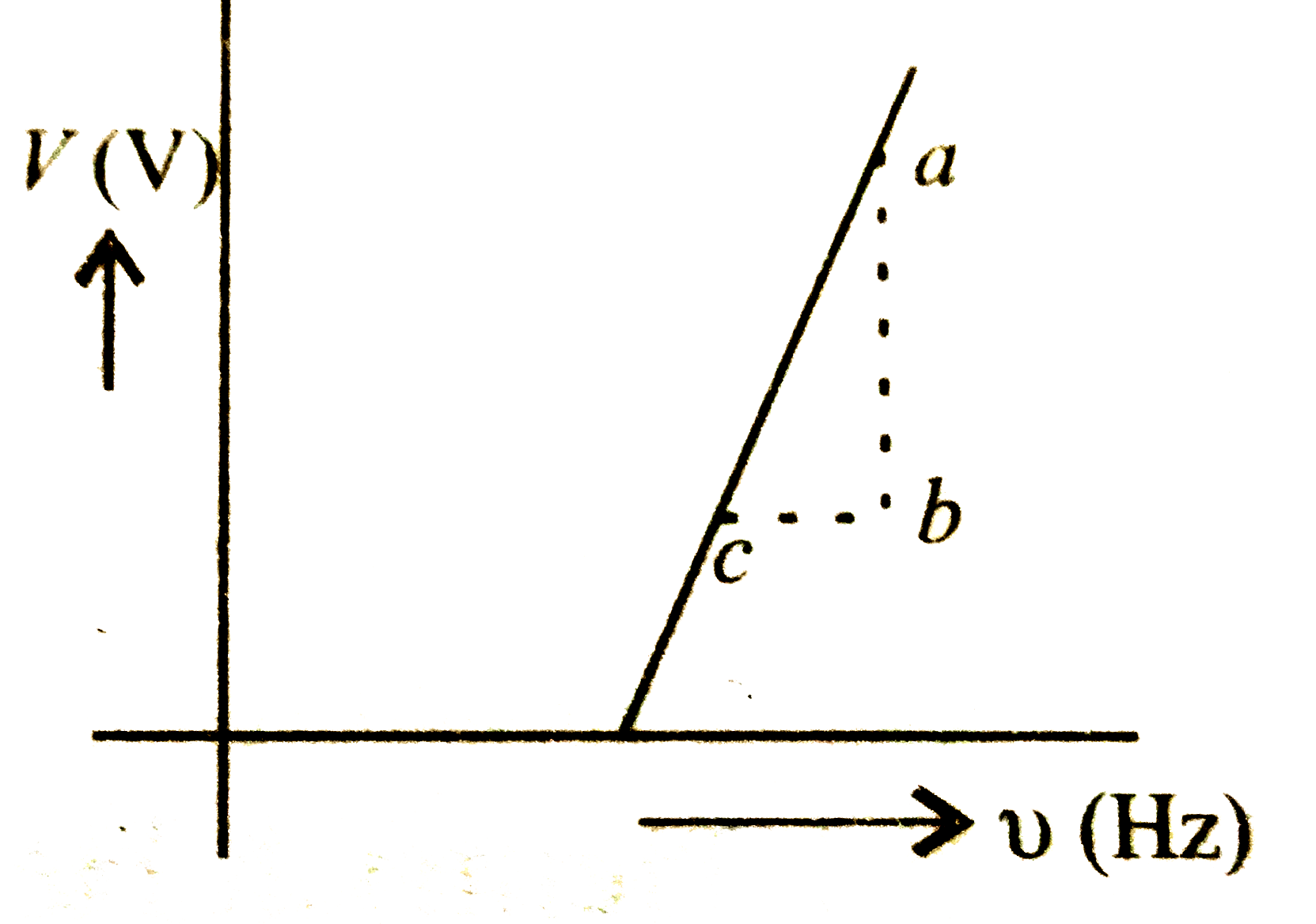 AeabbcBecbacCeacbcDeacab
AeabbcBecbacCeacbcDeacab
In a photoelectric experiment, the wavelength of the incident light is decreased from 6000A to 4000A. While the intensity of radiations remains the same,
View SolutionIn a photoelectric experiment, the wavelength of the light incident on a metal is changed from 300 nm to 400 nm. Choose the closest value of change in the stopping potential from given options (hce=1240nm.V)
View SolutionIn a photoelectric experiment, the wavelength of the light incident on a metal is changed from 300 nm to 400 nm. Choose the closest value of change in the stopping potential from given options (hce=1240nm.V)
View SolutionSuppose the wavelength of the incident light is increased from 3000Å to 3040Å. Find the corresponding change in the stopping potential. [Take the product hc=12.4×10−7eVm)]
View SolutionIn Young's double-slit experiment, the wavelength of light was changed from 7000Å to 3500 Å. While doubling the separation between the slits, which of the following is not true for this experiment?
View SolutionIn a given region of 10 fringes are observed in the reflected beam from a thin film. If the wavelength of th incident light is changed from 4200Å to 6000Å , then the number of fringes observed in the same region will be
View Solutionif the wavelength is chaged from4000A.→3000A, then stopping potential will become
View Solution
