A block of mass m is gently placed over a massive plank moving horizontal over a smooth surface with velocity 10ms−1. The coefficient of friction between the block and the plank is 0.2. The distance travelled by the block till it slides on the plank is [g=10ms−2]
10 m
15m
25 m
35m
The correct Answer is:C
To solve the problem step by step, we will use the work-energy theorem and the concepts of friction.
Step 1: Identify the given values
- Mass of the block, m=2kg (assumed from the transcript)
- Coefficient of friction, μ=0.2
- Initial velocity of the plank (and block), v=10ms−1
- Acceleration due to gravity, g=10ms−2
Step 2: Calculate the initial kinetic energy of the block
The initial kinetic energy (KEi) of the block is given by the formula:
KEi=12mv2
Substituting the values:
KEi=12×2kg×(10ms−1)2=12×2×100=100J
Step 3: Calculate the frictional force acting on the block
The frictional force (Fr) can be calculated using the formula:
Fr=μmg
Substituting the values:
Fr=0.2×2kg×10ms−2=0.2×20=4N
Step 4: Apply the work-energy theorem
According to the work-energy theorem, the work done by the frictional force is equal to the change in kinetic energy:
Work done by friction=KEf−KEi
Since the block comes to rest, KEf=0:
−KEi=−Fr⋅d
Where d is the distance traveled by the block until it slides. Rearranging gives:
Fr⋅d=KEi
Substituting the values we have:
4N⋅d=100J
Step 5: Solve for distance d
d=100J4N=25m
Conclusion
The distance traveled by the block until it slides on the plank is 25m.
---
- Mass of the block, m=2kg (assumed from the transcript)
- Coefficient of friction, μ=0.2
- Initial velocity of the plank (and block), v=10ms−1
- Acceleration due to gravity, g=10ms−2
The initial kinetic energy (KEi) of the block is given by the formula:
KEi=12mv2
Substituting the values:
KEi=12×2kg×(10ms−1)2=12×2×100=100J
The frictional force (Fr) can be calculated using the formula:
Fr=μmg
Substituting the values:
Fr=0.2×2kg×10ms−2=0.2×20=4N
According to the work-energy theorem, the work done by the frictional force is equal to the change in kinetic energy:
Work done by friction=KEf−KEi
Since the block comes to rest, KEf=0:
−KEi=−Fr⋅d
Where d is the distance traveled by the block until it slides. Rearranging gives:
Fr⋅d=KEi
Substituting the values we have:
4N⋅d=100J
d=100J4N=25m
The distance traveled by the block until it slides on the plank is 25m.
Similar Questions
A block of mass 2kg lying on ice when given a velocity of 6ms−1 is stopped by friction in 5s. The coefficient of friction between the block and ice is (g=10 ms−2)
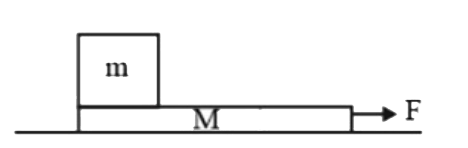
View SolutionA bolck of mass m =2 kg is placed on a plank of mass M = 10 kg, which is placed on a smooth horizontal plane as shown in the figure. The coefficient of friction between the block and the plank is μ=13. If a horizontal force F is applied on the plank, then the maximum value of F for which the block and the plank move together is (g=10m/s2)
View SolutionA block of mass 2 kg slides down an incline plane of inclination 30°. The coefficient of friction between block and plane is 0.5. The contact force between block and plank is :
View SolutionA 2kg block is placed over a 5kg block and both are placed on a smooth horizontal surface. The coefficient of friction between the blocks is 0.10. Find the acceleration of the two blocks if a horizontal force of 14N is applied to the upper block (g = 10ms−2).
View SolutionA block is gently placed on a conveyor belt moving horizontally with constant speed. After t = 4s, the velocity of the block becomes equal to the velocity of the belt. If the coefficient of friction between the block and the belt is μ=0.2, then the velocity of the conveyor belt is (g=10ms−2)
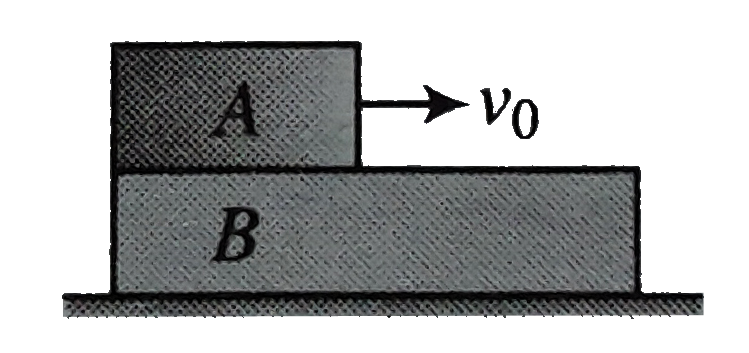
View SolutionA block A of mass m is placed over a plankB of mass 2m plank B is placed over a smooth horizontal surface .The coefficient of friction between A and B is 0.4 Block A is given a velocity v0 toward right Find acceleration (in ms−2 of B relative to A
View SolutionA block is kept on a rough horizontal plank. The coefficient of friction between the block and the plank is 12. The plank is undergoing SHM of angular frequency 10 rad/s. The maximum amplitude of plank in which the block does not slip over the plank is (g= 10 m/s2)
View SolutionA block A of mass m is placed over a plank B of mass 2m. Plank B is placed over a smooth horizontal surface. The coefficient of friction between A and B is 12 block A is given a velocity v0 towards right. Accelration of B relative to A is

View SolutionA small block of mass 1kg is placed over a plank of mass 2kg. The length of the plank is 2 m. coefficient of friction between the block and the plnak is 0.5 and the ground over which plank in placed is smooth. A constant force F=30N is applied on the plank in horizontal direction. the time after which the block will separte from the plank is (g=10m/s2)
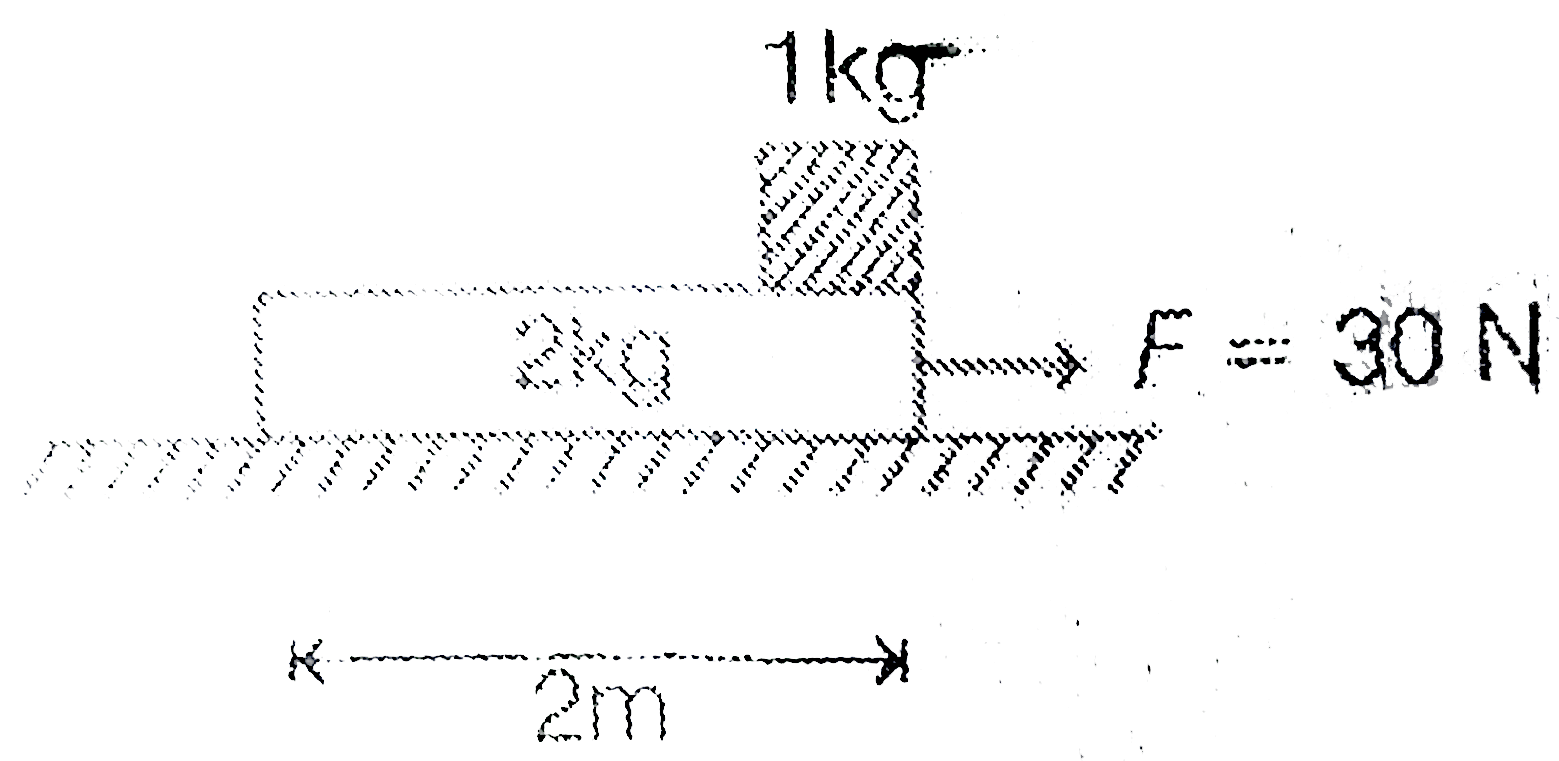
View SolutionA block of mass m=2kg of shown dimensions is placed on a plank of mass M = 6Kg which is placed on smooth horizontal plane. The coefficient of friction between the block and the plank is μ=13. If a horizontal froce F is applied on the plank, then find the maximum value of F (in N) for which the block and the plank move together

View Solution
