Resistance of 100Ω and 200Ω are connected in series with 220 V mains. When a voltmeter of 1000Ω resistance is connected in parallel to100Ω , then the reading of voltmeter is
82.5 volts
6.87 volts
587 .5 volts
58.75 volts
The correct Answer is:A
To solve the problem, we will follow these steps:
Step 1: Identify the Circuit Configuration
We have two resistors, R1=100Ω and R2=200Ω, connected in series with a voltage source of V=220V. A voltmeter with a resistance of Rv=1000Ω is connected in parallel to the 100Ω resistor.
Step 2: Calculate the Equivalent Resistance of the Parallel Combination
The voltmeter and the 100Ω resistor are in parallel. The formula for the equivalent resistance Req of two resistors in parallel is given by:
1Req=1R1+1Rv
Substituting the values:
1Req=1100+11000
Finding a common denominator (1000):
1Req=101000+11000=111000
Now, taking the reciprocal to find Req:
Req=100011Ω
Step 3: Calculate the Total Resistance in the Circuit
The total resistance Rtotal in the circuit is the sum of the equivalent resistance Req and the 200Ω resistor:
Rtotal=Req+R2=100011+200
To add these, convert 200 into a fraction with a denominator of 11:
200=220011
Now adding:
Rtotal=100011+220011=320011Ω
Step 4: Calculate the Current in the Circuit
Using Ohm's law, the current I flowing through the circuit can be calculated as:
I=VRtotal=220320011=220×113200
Calculating this gives:
I=24203200=121160A
Step 5: Calculate the Voltage Across the 100Ω Resistor
The voltage V100 across the 100Ω resistor (which is also the reading on the voltmeter) can be calculated using Ohm's law:
V100=I×Req=(121160)×(100011)
Calculating this gives:
V100=121×1000160×11=1210001760
Now simplifying:
V100=68.75V
Final Answer
The reading of the voltmeter is 68.75V.
---
We have two resistors, R1=100Ω and R2=200Ω, connected in series with a voltage source of V=220V. A voltmeter with a resistance of Rv=1000Ω is connected in parallel to the 100Ω resistor.
The voltmeter and the 100Ω resistor are in parallel. The formula for the equivalent resistance Req of two resistors in parallel is given by:
The total resistance Rtotal in the circuit is the sum of the equivalent resistance Req and the 200Ω resistor:
Using Ohm's law, the current I flowing through the circuit can be calculated as:
The voltage V100 across the 100Ω resistor (which is also the reading on the voltmeter) can be calculated using Ohm's law:
The reading of the voltmeter is 68.75V.
Similar Questions
50Ω and 100Ω resistors are connected in series. This connection is connected with a battery of 2.4 volts. When a voltmeter of 100Ω resistance is connected across 100Ω resistor, then the reading of the voltmeter will be
View SolutionThree bulbs of 40W,60Wand100W are connected in series with a 240V source.
View Solution
Knowledge Check
Two resistances R1=100±3ΩandR2=200±4Ω are connected in series . Find the equivalent resistance of the series combination.
A(66.7±1.8)ΩB(66.7±4.0)ΩC(66.7±3.0)ΩD(66.7±7.0)Ω
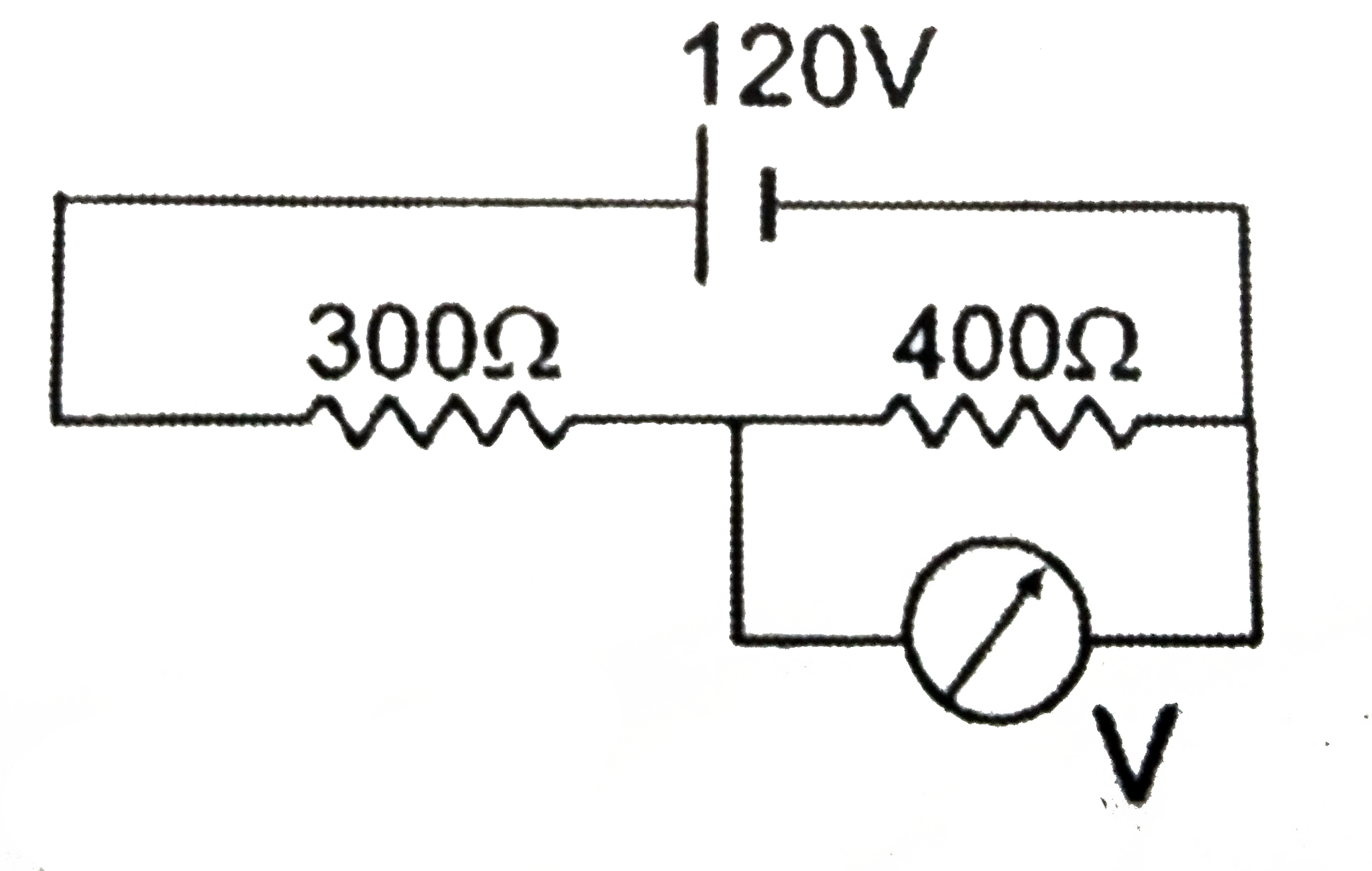
Two resistor 400Ω and 800Ω connected in series across a 6 V battery . Reading of Voltmeter of 10kΩ across 400Ω resistor is close to :
View SolutionTwo resistance of 400Ω and 800Ω are connected in series with 6 volt battery of negligible internal resistance. A voltmeter of resistance 10,000Ω is used to measure the potential difference across 400Ω. The error in measurement of potential difference in volts approximatley is
View SolutionTwo resistances R1=100±3ΩandR2=200±4Ω are connected in series . Find the equivalent resistance of the series combination.
View SolutionTwo resistances R_1, and R_2, each of 100 Omega 22 Omega are connected with potential source of 40 V between A and B. If resistance of voltmeter is 200 Omega, then reading of voltmeter is
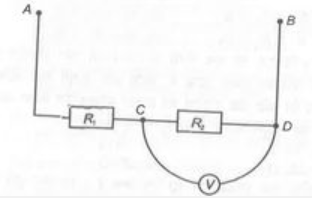
View SolutionIn the circuit shown, reading of the voltmeter connected across 400Ω resistance is 60 V. If it is connected across 300Ω resistance then reading in volt will be
View SolutionA cell of emf 3.4V and internal resistance 3Ω is connected to an ammeter having resistance 2Ω and to an external resistance of 100Ω. When a voltmeter is connected across the 100Ω resistance, the ammeter reading is 0.04A. Find the voltage reading by the voltmeter and its resistance. Had the voltmeter been an ideal one what would have been its reading?
View SolutionA cell of emf 3.4V and internal resistance 3Ω is connected to an ammeter having resistance 2Ω and to an external resistance of 100Ω. When a voltmeter is connected across the 100Ω resistance, the ammeter reading is 0.04A. Find the voltage reading by the voltmeter and its resistance. Had the voltmeter been an ideal one what would have been its reading?
View Solution
