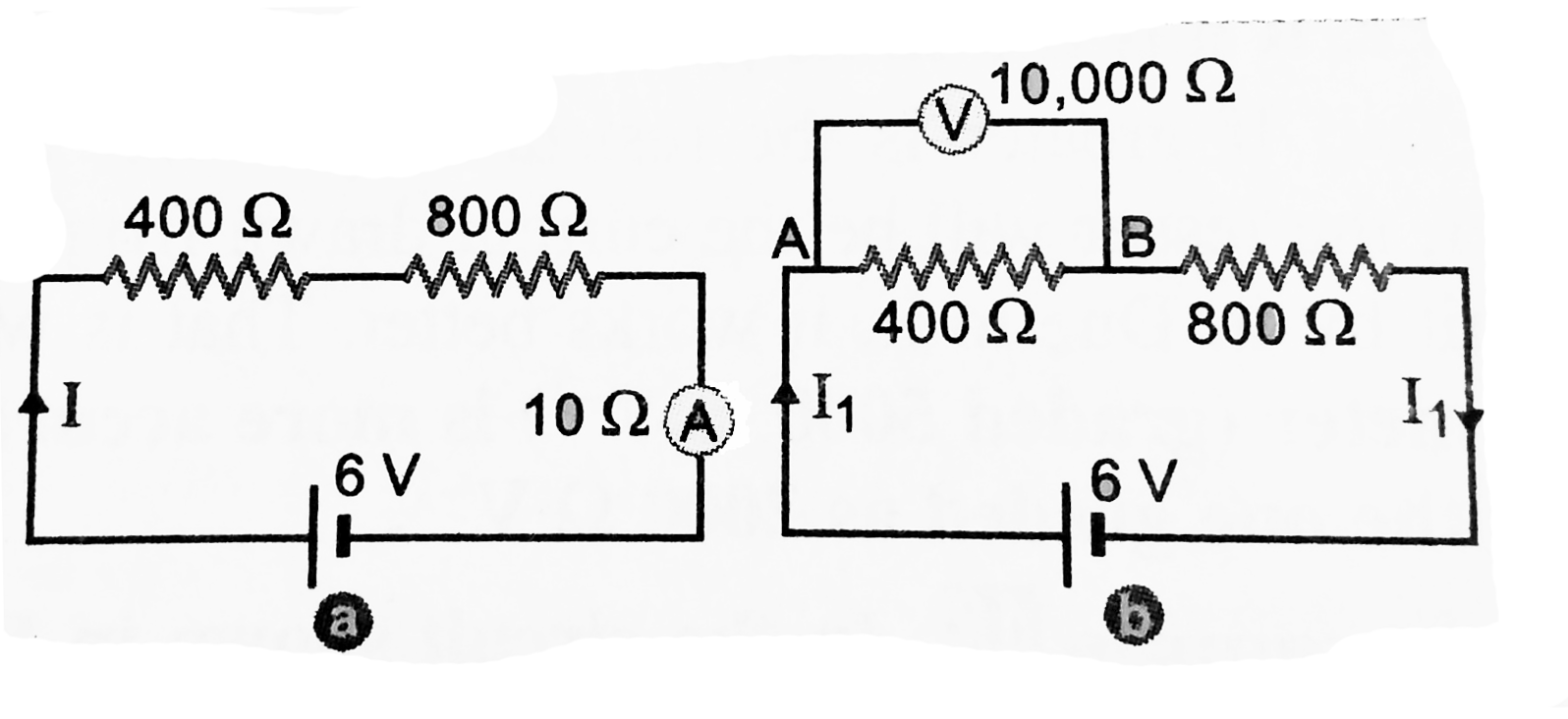
Two resistor 400Ω and 800Ω connected in series across a 6 V battery . Reading of Voltmeter of 10kΩ across 400Ω resistor is close to :
2V
1.95V
1.8 V
2.05V
To solve the problem, we need to find the reading of a voltmeter connected across a 400 Ω resistor in a series circuit with a 6 V battery and an 800 Ω resistor. The voltmeter has a resistance of 10 kΩ (10,000 Ω).
1. Identify the Total Resistance in the Circuit:
The total resistance (R_total) in the circuit is the sum of the two resistors in series:
Rtotal=R1+R2=400Ω+800Ω=1200Ω
2. Calculate the Total Current (I) in the Circuit:
Using Ohm's law, the current flowing through the circuit can be calculated as:
I=VRtotal=6V1200Ω=0.005A(5mA)
3. Calculate the Voltage Drop Across the 400 Ω Resistor:
The voltage drop (V_AB) across the 400 Ω resistor can be calculated using Ohm's law:
VAB=I×R1=0.005A×400Ω=2V
4. Calculate the Equivalent Resistance of the 400 Ω Resistor and the Voltmeter:
When the voltmeter is connected across the 400 Ω resistor, we need to find the equivalent resistance (R_eq) of the 400 Ω resistor and the voltmeter in parallel:
Req=R1×RvoltmeterR1+Rvoltmeter=400Ω×10,000Ω400Ω+10,000Ω
Req=400×10,00010,400≈384.6Ω
5. Calculate the New Current in the Circuit:
The new total resistance in the circuit will now include the equivalent resistance of the voltmeter:
Rnew total=Req+800Ω=384.6Ω+800Ω=1184.6Ω
Now, calculate the new current:
Inew=6V1184.6Ω≈0.00506A(5.06mA)
6. Calculate the Voltage Drop Across the 400 Ω Resistor with the Voltmeter Connected:
Now, we can find the voltage drop across the 400 Ω resistor with the voltmeter connected:
V′AB=Inew×R1=0.00506A×400Ω≈2.024V
7. Final Reading of the Voltmeter:
The reading of the voltmeter across the 400 Ω resistor will be approximately:
V′AB≈1.95V(rounded)
Conclusion:
The reading of the voltmeter across the 400 Ω resistor is approximately 1.95 V.
The total resistance (R_total) in the circuit is the sum of the two resistors in series:
Rtotal=R1+R2=400Ω+800Ω=1200Ω
Using Ohm's law, the current flowing through the circuit can be calculated as:
I=VRtotal=6V1200Ω=0.005A(5mA)
The voltage drop (V_AB) across the 400 Ω resistor can be calculated using Ohm's law:
VAB=I×R1=0.005A×400Ω=2V
When the voltmeter is connected across the 400 Ω resistor, we need to find the equivalent resistance (R_eq) of the 400 Ω resistor and the voltmeter in parallel:
Req=R1×RvoltmeterR1+Rvoltmeter=400Ω×10,000Ω400Ω+10,000Ω
Req=400×10,00010,400≈384.6Ω
The new total resistance in the circuit will now include the equivalent resistance of the voltmeter:
Rnew total=Req+800Ω=384.6Ω+800Ω=1184.6Ω
Now, calculate the new current:
Inew=6V1184.6Ω≈0.00506A(5.06mA)
Now, we can find the voltage drop across the 400 Ω resistor with the voltmeter connected:
V′AB=Inew×R1=0.00506A×400Ω≈2.024V
The reading of the voltmeter across the 400 Ω resistor will be approximately:
V′AB≈1.95V(rounded)
The reading of the voltmeter across the 400 Ω resistor is approximately 1.95 V.
Topper's Solved these Questions
Similar Questions
Three resistors of 2Ω,3Ω and 4Ω are connected in
series
View SolutionTwo resistors 400Ω and 800Ω are connected in series with a 6V battery. It is desired to measure the current in the circuit. An ammeter of 10Ω resistance is used for this purpose figure. What will be the reading in the ammeter? Similarly, if a voltmeter of 10,000Ω resistance is used to measure the potential difference across the 400Ω resistor, what will be the reading in the voltmeter?
View SolutionTwo resistors of 6Ω and 9Ω are connected in series to a 120 V source. The power consumed by the 6Ω resistor is
View SolutionIn an electrical circuit, two resistors of 2Ωand4Ω respectively are connected in series to a 6V battery. The heat dissipated by the 4Ω resistor in 5s will be :
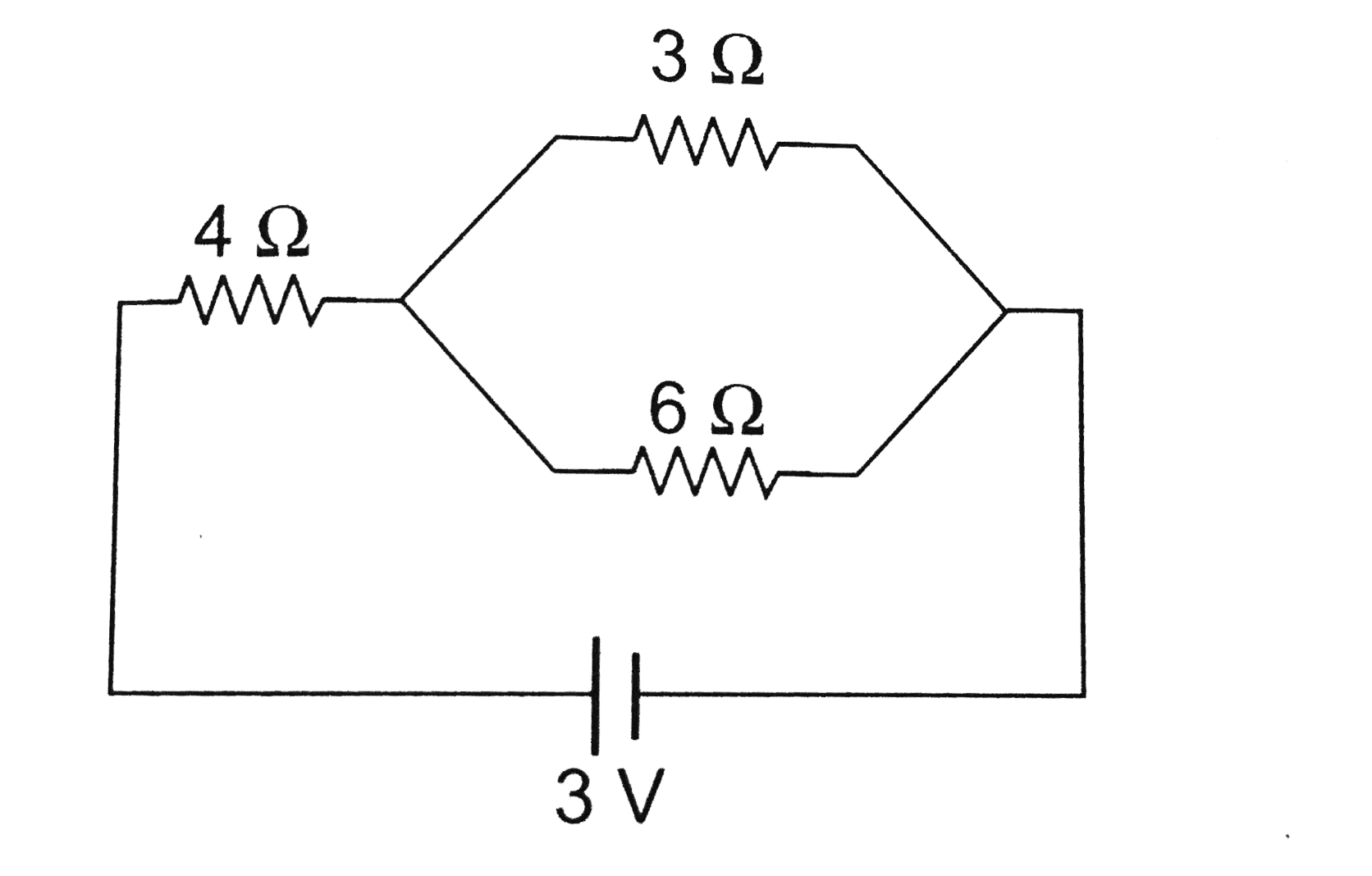
View SolutionThe potential drop across the 3Ω resistor is
View SolutionTwo resistance of 400Ω and 800Ω are connected in series with 6 volt battery of negligible internal resistance. A voltmeter of resistance 10,000Ω is used to measure the potential difference across 400Ω. The error in measurement of potential difference in volts approximatley is
View SolutionTwo resistors of resistances 2Ωand4Ω when connected to a battery will have :
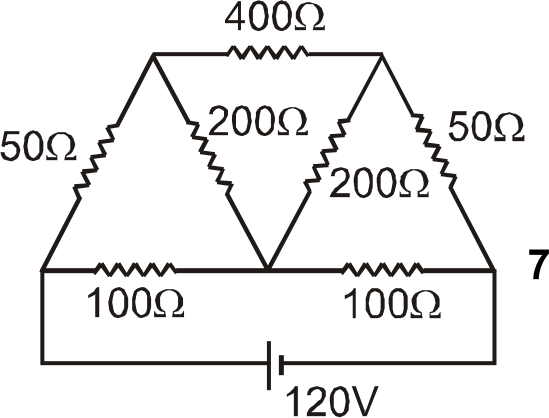
View SolutionElectric current through 400Ω resistor is :
View SolutionTwo resistors of 10KΩ and 20KΩ are conne cted in series. If tolerance of each resistor is 10% then tolerance of the combination will be
View SolutionResistance of 100Ω and 200Ω are connected in series with 220 V mains. When a voltmeter of 1000Ω resistance is connected in parallel to100Ω , then the reading of voltmeter is
View Solution