Two stationary sources of sound, S1 and S2 having an equal frequency are fixed some distance apart. The position A is left of S1 , position B in the middle of the two sources and positionC is to the right of S2. An observer starts moving with velocity V0 from position A towards S1, then
beats for three position A,B and C will be heard
beats will be heard from A and C but not in case of B
beats will be not heard for A and C but will be heard for B
beats will be not heard for three position of A,B and C
The correct Answer is:C
To solve the problem, we need to analyze the situation involving two stationary sound sources, S1 and S2, and an observer moving towards S1 from position A. We will use the principles of the Doppler effect and the concept of beats.
1. Understanding the Setup:
- We have two stationary sound sources, S1 and S2, which emit sound waves of equal frequency f.
- The observer starts from position A (to the left of S1) and moves towards S1.
2. Doppler Effect at Position A:
- As the observer moves towards S1, the apparent frequency f′ heard by the observer can be calculated using the Doppler effect formula:
f′=f(v+v0v)
where v is the speed of sound in air, and v0 is the velocity of the observer towards the source.
- Since the observer is also moving towards S2, the apparent frequency from S2 can be calculated similarly:
f′′=f(v+v0v)
- Since both sources have the same frequency and the observer is moving towards both sources, the change in frequency (or beat frequency) will be:
Δf=f′−f′′=0
- Therefore, at position A, the beats are unheard (as there is no difference in frequency).
3. Doppler Effect at Position B:
- At position B (the midpoint between S1 and S2), the observer is moving towards S1 and away from S2.
- The frequency from S1 will increase:
f′=f(v+v0v)
- The frequency from S2 will decrease:
f′′=f(v−v0v)
- The change in frequency (beat frequency) will be:
Δf=f′−f′′=f(v+v0v)−f(v−v0v)=f(2v0v)
- Thus, at position B, beats will be heard.
4. Doppler Effect at Position C:
- At position C (to the right of S2), the observer is moving away from both sources.
- The frequency from S1 will decrease:
f′=f(v−v0v)
- The frequency from S2 will also decrease:
f′′=f(v−v0v)
- The change in frequency (beat frequency) will be:
Δf=f′−f′′=0
- Therefore, at position C, the beats are unheard.
5. Conclusion:
- The beats are unheard at positions A and C, and heard at position B.
- Therefore, the correct answer is that beats will be heard at position B and not at positions A and C.
Final Answer:
The beats will be heard at position B, but not at positions A and C.
- We have two stationary sound sources, S1 and S2, which emit sound waves of equal frequency f.
- The observer starts from position A (to the left of S1) and moves towards S1.
- As the observer moves towards S1, the apparent frequency f′ heard by the observer can be calculated using the Doppler effect formula:
f′=f(v+v0v)
where v is the speed of sound in air, and v0 is the velocity of the observer towards the source.
- Since the observer is also moving towards S2, the apparent frequency from S2 can be calculated similarly:
f′′=f(v+v0v)
- Since both sources have the same frequency and the observer is moving towards both sources, the change in frequency (or beat frequency) will be:
Δf=f′−f′′=0
- Therefore, at position A, the beats are unheard (as there is no difference in frequency).
- At position B (the midpoint between S1 and S2), the observer is moving towards S1 and away from S2.
- The frequency from S1 will increase:
f′=f(v+v0v)
- The frequency from S2 will decrease:
f′′=f(v−v0v)
- The change in frequency (beat frequency) will be:
Δf=f′−f′′=f(v+v0v)−f(v−v0v)=f(2v0v)
- Thus, at position B, beats will be heard.
- At position C (to the right of S2), the observer is moving away from both sources.
- The frequency from S1 will decrease:
f′=f(v−v0v)
- The frequency from S2 will also decrease:
f′′=f(v−v0v)
- The change in frequency (beat frequency) will be:
Δf=f′−f′′=0
- Therefore, at position C, the beats are unheard.
- The beats are unheard at positions A and C, and heard at position B.
- Therefore, the correct answer is that beats will be heard at position B and not at positions A and C.
The beats will be heard at position B, but not at positions A and C.
Similar Questions
Two coherent sources S1 and S2 are separated by a small distance d. The fringes obtained on the screen will be:
View SolutionA particle starts moving with constant, velocity v=2ms, from position x=5m The position time graph will be
View SolutionTwo sources S1 and S2 of sound having frequencies 338Hz and 342Hz are separated by a large distance. The speed of sound is 340 ms^(-1). With what velocity should an observer move from source S2→S1 so that he hears no beats?
View SolutionS1 and S2 are two sources of sound emitting sine waves. The two sources are in phase. The sound emitted by the two sources interfers at point F. The waves of wavelength :

View SolutionConsider two sound sources S1 and S2 having same frequency 100Hz and the observer O located between them as shown in the fig. All the three are moving with same velocity in same direction. The beat frequency of the observer is

View SolutionTwo sources of sound S1 and S2 produce sound waves of same frequency 660Hz. A listener is moving from source S1 towards S2 with a constant speed um/s and he hears 10 beats/s. The velocity of sound is 330m/s. Then, u equals :
View SolutionTwo source of sound, S1 and S2, emitting waves of equal wavelength 2cm, are placed with a separation of 3cm between them. A detector can be moved on a line parallel to S1S2 and at a distance 24cm from it. Initially, the detecor is equidistant from the two sources. Assuming that the waves emitted by the sources are in phase, find the minimum distance through which the detector should be shifted to detect a minimum of sound.
View SolutionConsider two coherent, monochromatic (wavelength λ) sources S1andS2, separated by a distance d. The ratio of intensities of S1 and that of S2 (which is responsible for interference at point P, where detector is located) is 4. The distance of point P from S1 is (if the resultant intensity at point P is equal to 94 times of intensity of S1) (Given : ∠S2S1P=90∘,d>0andn is a positive integer)
View SolutionA stationary source emits sound of frequency 1200 Hz. If would blows at the speed of 0.1 v. deduce
(a) The change in the frequency for a stationary observer on the wind side of the source
(b) Report the calculations for the case when there is no wind but the observer moves at 0.1 v speed towards the source (Given : velocity of sound = v)
View Solution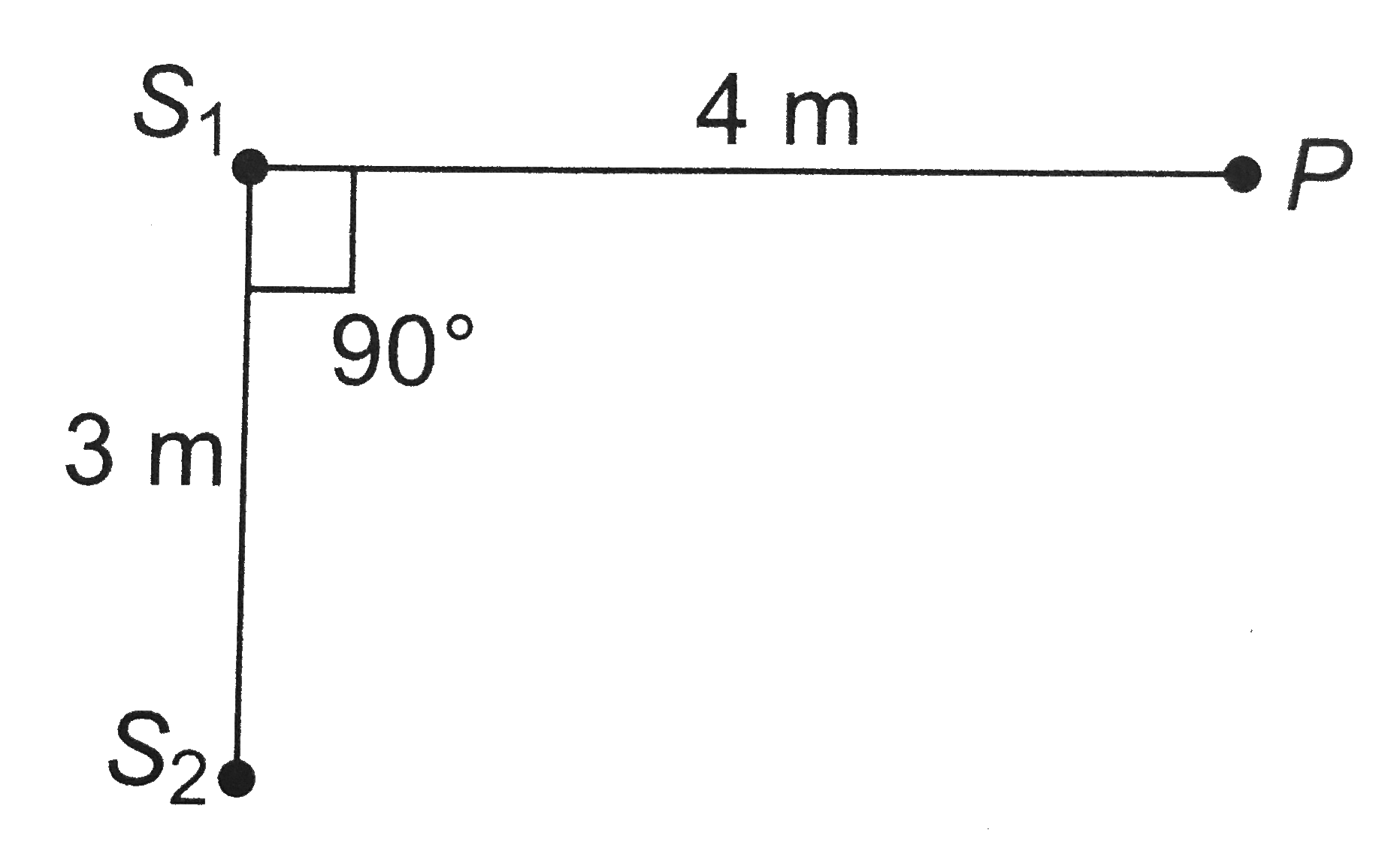
S1 and S2 are two coherent sources of sound of frequency 110Hz each they have no initial phase difference. The intensity at a point P due to S1 is I0 and due to S2 is 4I0. If the velocity of sound is 330m/s then the resultant intensity at P is
View Solution
