A body of mass m collides against a wall with the velocity v and rebounds with the same speed. Its magnitude of change of momentum is
2 m v
m v
12mv
0
The correct Answer is:A
To find the magnitude of the change in momentum of a body of mass m that collides with a wall with velocity v and rebounds with the same speed, we can follow these steps:
1. Identify Initial Momentum:
- The initial momentum of the body before collision can be calculated using the formula:
Initial Momentum=m⋅v
- Here, we consider the direction towards the wall as positive, so the initial momentum is:
pinitial=mv
2. Identify Final Momentum:
- After colliding with the wall, the body rebounds with the same speed v but in the opposite direction. Therefore, the final momentum will be:
Final Momentum=m⋅(−v)=−mv
3. Calculate Change in Momentum:
- The change in momentum (Δp) is given by the difference between the final momentum and the initial momentum:
Δp=pfinal−pinitial=(−mv)−(mv)
- Simplifying this gives:
Δp=−mv−mv=−2mv
4. Determine the Magnitude of Change in Momentum:
- Since we are interested in the magnitude of the change in momentum, we take the absolute value:
|Δp|=|−2mv|=2mv
Thus, the magnitude of the change in momentum is 2mv.
Final Answer:
Magnitude of change in momentum=2mv
---
- The initial momentum of the body before collision can be calculated using the formula:
Initial Momentum=m⋅v
- Here, we consider the direction towards the wall as positive, so the initial momentum is:
pinitial=mv
- After colliding with the wall, the body rebounds with the same speed v but in the opposite direction. Therefore, the final momentum will be:
Final Momentum=m⋅(−v)=−mv
- The change in momentum (Δp) is given by the difference between the final momentum and the initial momentum:
Δp=pfinal−pinitial=(−mv)−(mv)
- Simplifying this gives:
Δp=−mv−mv=−2mv
- Since we are interested in the magnitude of the change in momentum, we take the absolute value:
|Δp|=|−2mv|=2mv
Magnitude of change in momentum=2mv
Similar Questions
A body of mass 2kg collides with a wall with speed 100 m/s and rebounds with same speed. If the time of contact was 1/50 second, the force exerted on the wall is
View SolutionA particle of mass m strikes elastically on a wall with velocity v, at an angle of 60∘ from the wall then magnitude of change in momentum of ball along the wall is
View Solution
Knowledge Check
A ball of mass m collides with a wall with speed v and rebounds on the same line with the same speed. If the mass of the wall is taken as infinite, then the work done by the ball on the wall is
Amv2B12mv2C2mvDzeroA ball of mass m strikes a rigid walJ with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is
A2muBmuCzeroD−2muA ball of mass m strikes a rigid walJ with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is
 Amu sin30∘tB2mu sin30∘tCmu cos30∘tD2mu cos30∘t
Amu sin30∘tB2mu sin30∘tCmu cos30∘tD2mu cos30∘t
A mass m with velocity u strikes a wall normally and returns with same speed. What is the magnitude of the change in momentum of the body when it returns.
View SolutionAn object of m kg with speed of v ms−1 strikes a wall at an angle θ and rebounds at the same speed and same angle. Find the magnitude of change in the momentum of object.
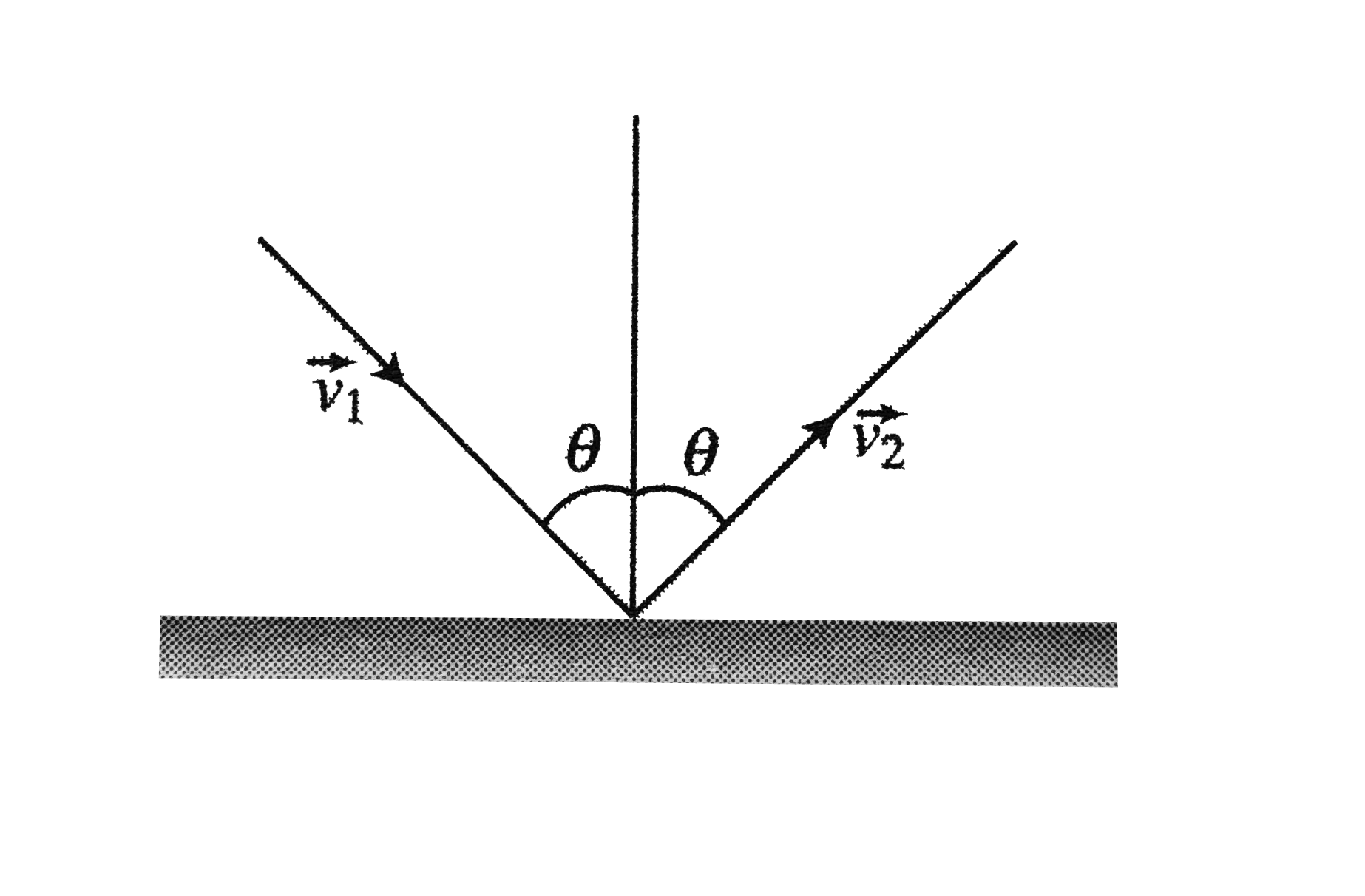
View SolutionAn object of m kg with speed of v ms−1 strikes a wall at an angle θ and rebounds at the same speed and same angle. Find the magnitude of change in the momentum of object.

View SolutionA ball of mass 600 gm strikes a wall with a velocity of 5ms−1 at an angle 30∘ with the wall and rebounds with the same speed at the same angle with the wall. The change in momentum of the ball is, (in kg ms−1)
View Solution
A smooth wedge of mass M is pushed with an acceleration a=>anθ and a block of mass m is projected down the slant with a velocity v relative to the wedge.
The horizontal force applied on the wedge is:
View Solution
