A body of mass 2kg collides with a wall with speed 100 m/s and rebounds with same speed. If the time of contact was 1/50 second, the force exerted on the wall is
104N
4N
2×104N
8N
The correct Answer is:C
To solve the problem, we need to calculate the force exerted on the wall when a body collides with it and rebounds. We will use the concept of momentum and the formula for force.
1. Identify the given values:
- Mass of the body (m) = 2 kg
- Initial speed (u) = 100 m/s (towards the wall)
- Final speed (v) = -100 m/s (away from the wall, hence negative)
- Time of contact (Δt) = 1/50 seconds
2. Calculate the initial momentum (p_initial):
pinitial=m⋅u=2kg⋅100m/s=200kg m/s
3. Calculate the final momentum (p_final):
pfinal=m⋅v=2kg⋅(−100)m/s=−200kg m/s
4. Calculate the change in momentum (Δp):
Δp=pfinal−pinitial=−200kg m/s−200kg m/s=−400kg m/s
5. Calculate the force (F) using the formula:
F=ΔpΔt
Substituting the values:
F=−400kg m/s1/50s=−400kg m/s⋅50=−20000N
6. Express the force in magnitude:
The magnitude of the force exerted on the wall is:
|F|=20000N=2×104N
Final Answer:
The force exerted on the wall is 2×104N.
---
- Mass of the body (m) = 2 kg
- Initial speed (u) = 100 m/s (towards the wall)
- Final speed (v) = -100 m/s (away from the wall, hence negative)
- Time of contact (Δt) = 1/50 seconds
pinitial=m⋅u=2kg⋅100m/s=200kg m/s
pfinal=m⋅v=2kg⋅(−100)m/s=−200kg m/s
Δp=pfinal−pinitial=−200kg m/s−200kg m/s=−400kg m/s
F=ΔpΔt
Substituting the values:
F=−400kg m/s1/50s=−400kg m/s⋅50=−20000N
The magnitude of the force exerted on the wall is:
|F|=20000N=2×104N
The force exerted on the wall is 2×104N.
Similar Questions
A body of mass m collides against a wall with the velocity v and rebounds with the same speed. Its magnitude of change of momentum is
View SolutionA ball of mass 2 kg is moving with velocity 20 m/sec strikes with the surface and rebounds with same speed, if time of contact is 0.1 sec then calculate average force on the ball.
View Solution
Knowledge Check
A ball of mass m collides with a wall with speed v and rebounds on the same line with the same speed. If the mass of the wall is taken as infinite, then the work done by the ball on the wall is
Amv2B12mv2C2mvDzeroA ball of mass m strikes a rigid walJ with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is
A2muBmuCzeroD−2muA ball of mass m strikes a rigid walJ with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is
 Amu sin30∘tB2mu sin30∘tCmu cos30∘tD2mu cos30∘t
Amu sin30∘tB2mu sin30∘tCmu cos30∘tD2mu cos30∘t
A spherical ball of mass 10−6 kg hits a wall 1000 times per second normally with a velocity of 1000 m/s and rebounds with same velocity along the initial direction. The force experienced by the wall is
View SolutionA ball of mass 0.5kg moving with a velocity of 2m/s strikes a wall normally and bounces back with the same speed . If the time of contact between the ball and the wall is 1 millisecond , the average force exerted by the wall on the ball is
View SolutionA ball of mass 0.5kg moving with a velocity of 2m/s strikes a wall normally and bounces back with the same speed . If the time of contact between the ball and the wall is 1 millisecond , the average force exerted by the wall on the ball is
View SolutionA ball of mass 'm' is thrown with a speed v0 towards a bat. It rebounds along the same speed 2v0 . The variation of interaction force between the bat and ball is shown
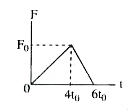
Average force exerted by the bat on the ball is
View SolutionA ball of mass 'm' is thrown with a speed v0 towards a bat. It rebounds along the same speed 2v0 . The variation of interaction force between the bat and ball is shown
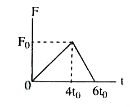
Maximum force exerted by the bat on the ball is
View Solution
