A battery of 10V is connected to a capacitor of capacity 0.lF. The battery is now removed and this capacitor is connected to a second uncharged capacitor. If the charges are distributed equally on these two capacitors, find the total energy stored in the two capacitors. Find the ratio of final energy to initial energy stored in capacitors.
The correct Answer is:52J.UinitialUfinal=52.5=2
To solve the problem step by step, we will follow these calculations:
Step 1: Calculate the initial charge on the capacitor
The initial charge Q on the capacitor can be calculated using the formula:
Q=C×V
where:
- C=0.1F (capacitance)
- V=10V (voltage)
Substituting the values:
Q=0.1F×10V=1C
Step 2: Calculate the initial energy stored in the capacitor
The initial energy Uinitial stored in the capacitor can be calculated using the formula:
U=12CV2
Substituting the values:
Uinitial=12×0.1F×(10V)2=12×0.1×100=5J
Step 3: Connect the charged capacitor to an uncharged capacitor
When the charged capacitor is connected to an uncharged capacitor, the total capacitance becomes:
Ctotal=C1+C2=0.1F+0.1F=0.2F
The charge Q remains the same, but the voltage across both capacitors will change.
Step 4: Calculate the final voltage across the capacitors
The final voltage Vf across the capacitors can be found using the formula:
Vf=QCtotal
Substituting the values:
Vf=1C0.2F=5V
Step 5: Calculate the final energy stored in the capacitors
The final energy Ufinal stored in the two capacitors can be calculated using:
Ufinal=12CtotalV2f
Substituting the values:
Ufinal=12×0.2F×(5V)2=12×0.2×25=2.5J
Step 6: Calculate the total energy stored in both capacitors
The total energy stored in both capacitors is:
Utotal=Uinitial+Ufinal=5J+2.5J=7.5J
Step 7: Calculate the ratio of final energy to initial energy
The ratio of the final energy to the initial energy is:
Ratio=UfinalUinitial=2.5J5J=12
Final Answers:
- Total energy stored in the two capacitors: 7.5 J
- Ratio of final energy to initial energy: 1:2
The initial charge Q on the capacitor can be calculated using the formula:
Q=C×V
where:
- C=0.1F (capacitance)
- V=10V (voltage)
Q=0.1F×10V=1C
The initial energy Uinitial stored in the capacitor can be calculated using the formula:
U=12CV2
Substituting the values:
Uinitial=12×0.1F×(10V)2=12×0.1×100=5J
When the charged capacitor is connected to an uncharged capacitor, the total capacitance becomes:
Ctotal=C1+C2=0.1F+0.1F=0.2F
The charge Q remains the same, but the voltage across both capacitors will change.
The final voltage Vf across the capacitors can be found using the formula:
Vf=QCtotal
Substituting the values:
Vf=1C0.2F=5V
The final energy Ufinal stored in the two capacitors can be calculated using:
Ufinal=12CtotalV2f
Substituting the values:
Ufinal=12×0.2F×(5V)2=12×0.2×25=2.5J
The total energy stored in both capacitors is:
Utotal=Uinitial+Ufinal=5J+2.5J=7.5J
The ratio of the final energy to the initial energy is:
Ratio=UfinalUinitial=2.5J5J=12
- Total energy stored in the two capacitors: 7.5 J
- Ratio of final energy to initial energy: 1:2
Topper's Solved these Questions
Similar Questions
Find the total energy stored in the capacitors in the given network.
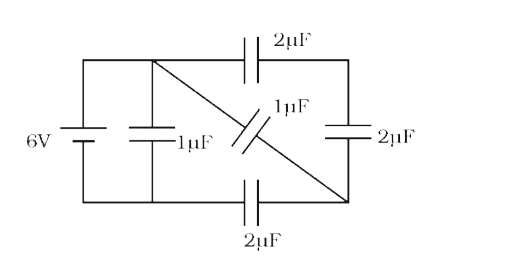
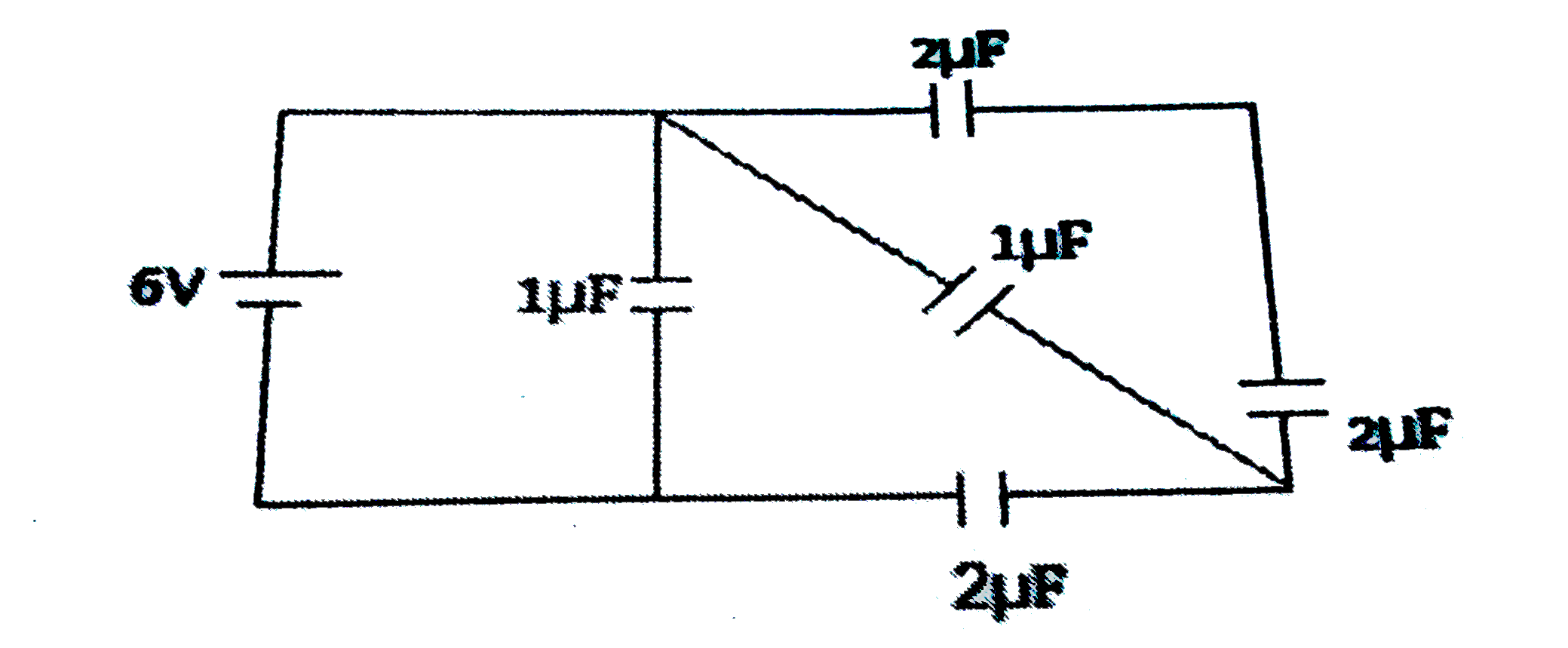
View SolutionFind total energy stored in capacitors given in the circuit
View SolutionA capacitor of capacitance 5μF is charged to potential 20V and isolated. Now, an uncharged capacitor is connected in parallel to it. If the charge distributes equally on these capacitors, find total energy stored in capacitors.
View SolutionFind the charge stored in the capacitor.
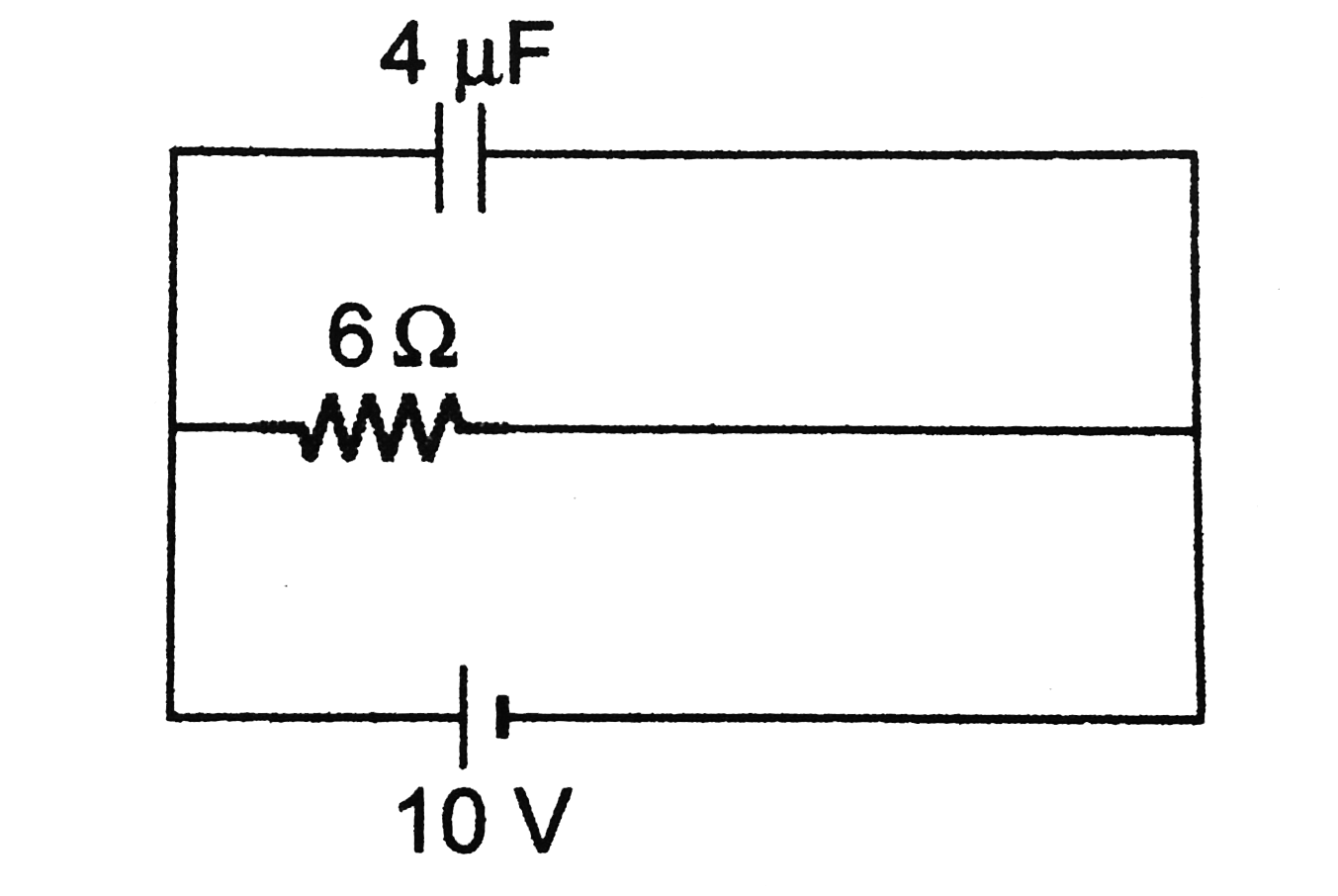
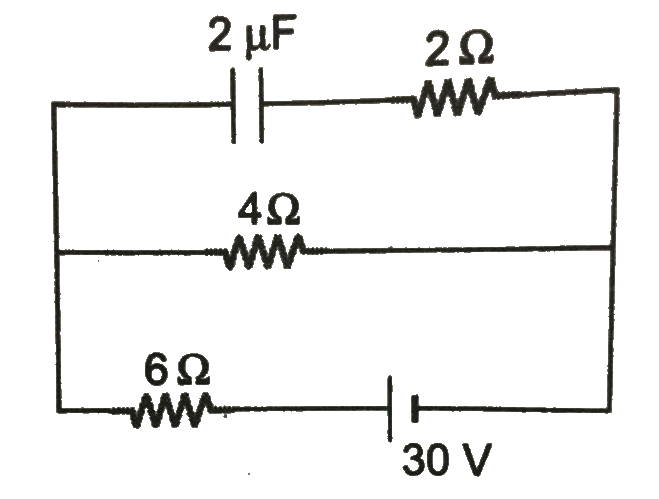
View SolutionFind the charge stored in the capacitor.
View SolutionA capacitor of 60 pF charged to 20 volt. Now battery is removed and then this capacitor is connected to another identical uncharged capacitor. Find heat loss in nJ
View SolutionA capacitor of 60 pF charged to 20 volt. Now battery is removed and then this capacitor is connected to another identical uncharged capacitor. Find heat loss in nJ
View SolutionThe total electrostatic energy stored in both the capacitor is
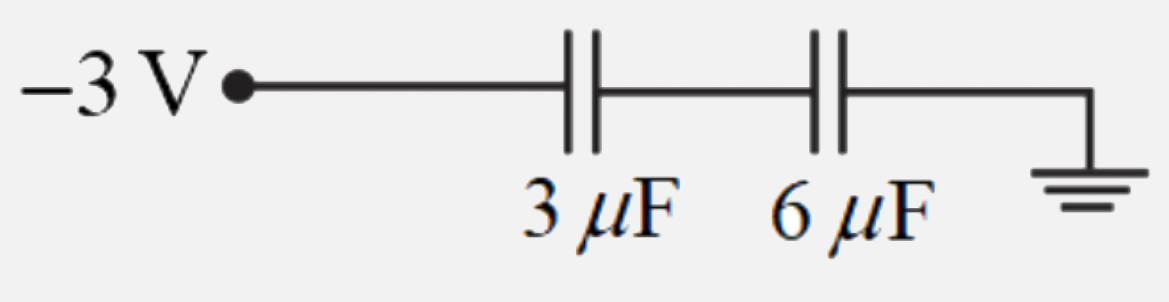
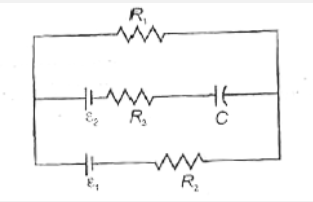
View SolutionFind the charge and energy stored on the capacitor C in the following circuit.
View SolutionA capacitor is charge until it stores an energy of 1J. A second uncharged capacitor is connected to it, so that charge districutes equally. The final energy stored in the second capacitor is
View Solution
