A variable force F acts along the x - axis given by F=(3x2)−2x+1N. The work done by the force when a particle of mass 100 g moves from x = 50 cm to x = 100 cm is
(a)0.625 J
(b)6.25 J
(c)0.0625 J
(d)62.5 J
The correct Answer is:A
To solve the problem of finding the work done by the variable force F=3x2−2x+1 when a particle of mass 100 g moves from x=50 cm to x=100 cm, we can follow these steps:
1. Convert Units:
- The mass of the particle is given as 100 g, which is 0.1 kg (since 1 g = 0.001 kg).
- The distance needs to be converted from centimeters to meters:
- x=50 cm = 0.5 m
- x=100 cm = 1 m
2. Set Up the Work Done Integral:
- The work done W by a variable force is given by the integral of the force over the displacement:
W=∫x2x1Fdx
- Here, F=3x2−2x+1, x1=0.5, and x2=1.
3. Integrate the Force Function:
- We need to calculate:
W=∫10.5(3x2−2x+1)dx
- The integral can be calculated as follows:
W=(x3−x2+x)10.5
4. Evaluate the Integral at the Limits:
- First, evaluate at the upper limit x=1:
W(1)=13−12+1=1−1+1=1
- Now evaluate at the lower limit x=0.5:
W(0.5)=(0.5)3−(0.5)2+(0.5)=18−14+12
- Converting to a common denominator (8):
W(0.5)=18−28+48=1−2+48=38
5. Calculate the Work Done:
- Now, subtract the two results:
W=W(1)−W(0.5)=1−38=88−38=58
- Therefore, the work done is:
W=0.625J
Final Answer:
The work done by the force when the particle moves from x=50 cm to x=100 cm is 0.625J.
---
- The mass of the particle is given as 100 g, which is 0.1 kg (since 1 g = 0.001 kg).
- The distance needs to be converted from centimeters to meters:
- x=50 cm = 0.5 m
- x=100 cm = 1 m
- The work done W by a variable force is given by the integral of the force over the displacement:
W=∫x2x1Fdx
- Here, F=3x2−2x+1, x1=0.5, and x2=1.
- We need to calculate:
W=∫10.5(3x2−2x+1)dx
- The integral can be calculated as follows:
W=(x3−x2+x)10.5
- First, evaluate at the upper limit x=1:
W(1)=13−12+1=1−1+1=1
- Now evaluate at the lower limit x=0.5:
W(0.5)=(0.5)3−(0.5)2+(0.5)=18−14+12
- Converting to a common denominator (8):
W(0.5)=18−28+48=1−2+48=38
- Now, subtract the two results:
W=W(1)−W(0.5)=1−38=88−38=58
- Therefore, the work done is:
W=0.625J
The work done by the force when the particle moves from x=50 cm to x=100 cm is 0.625J.
Similar Questions
Knowledge Check
- Question 1 - Select One
A force F is related to the position of a particle by the relation F=(10x2)N . Find the work done by the force when the particle moves from x=2m→x=4m.
A563 JB560 JC5603 JD3560 J - Question 2 - Select One
A force F acting on an object varies with distance x as shown in the figure. The work done by the force in moving the object from x=0 to x = 20 m is
 A500 JB1000 JC1500 JD2000 J
A500 JB1000 JC1500 JD2000 J
A particle moves along x - axis under the action of a position dependent force F=(5x2−2x)N. Work done by force on the particle when it moves from origin to x = 3 m is
View SolutionA particle is subjected to a force Fx that varies withes position as shown in figure. Find the work done by the force on the body as it moves
(a) from x=10.0m to x=5.0m,
(b) from x=5.0m to x=10.0m,
(c ) from x=10.0m to x=15.0m,
(d) what is the total work done by the force over the distance x=0 to x=15.0?
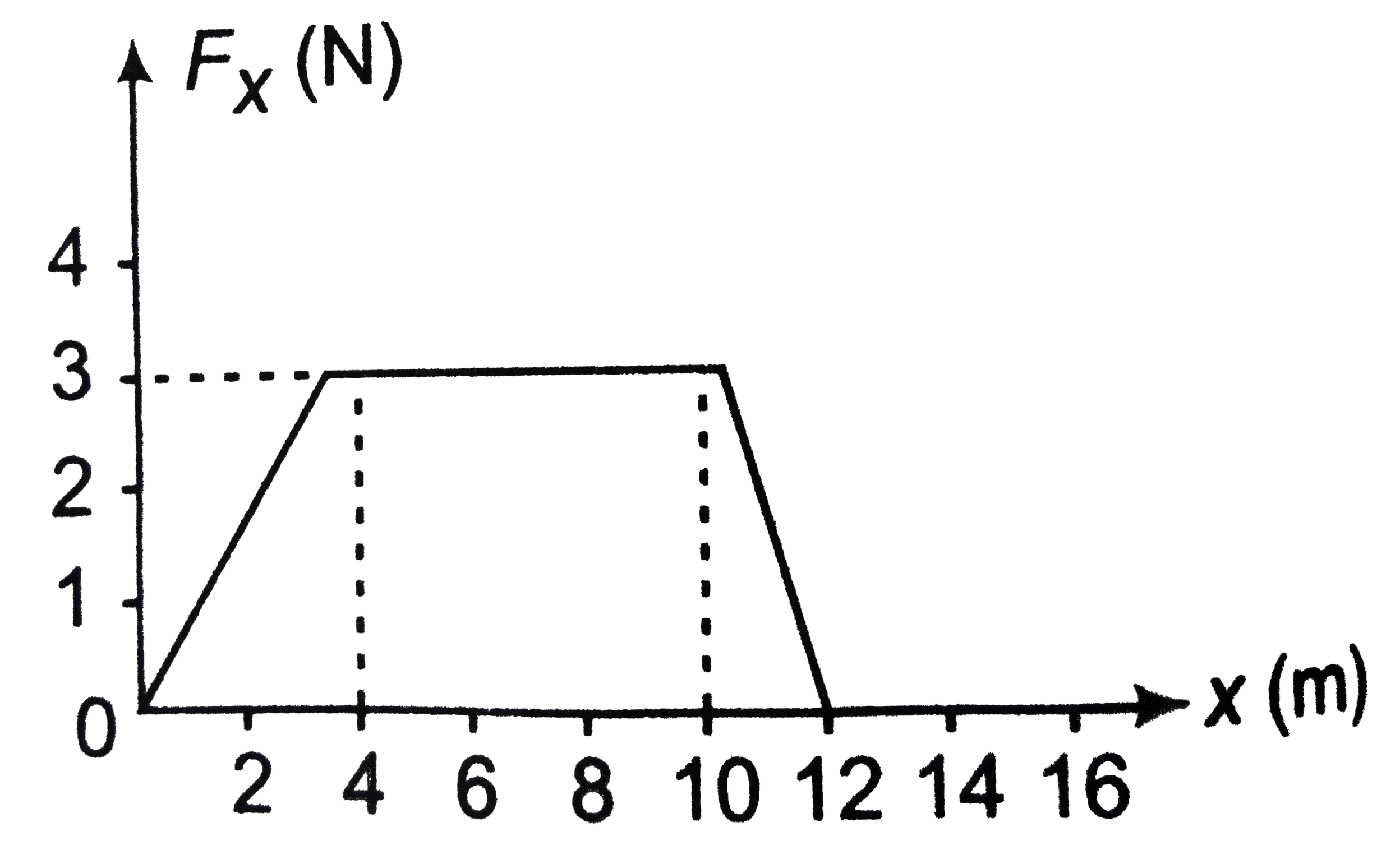 .View Solution
.View SolutionA Force F acting on an object varies with distance x as shown in the here . The force is in newton and x in metre. The work done by the force in moving the object from x=0 to x=6m is
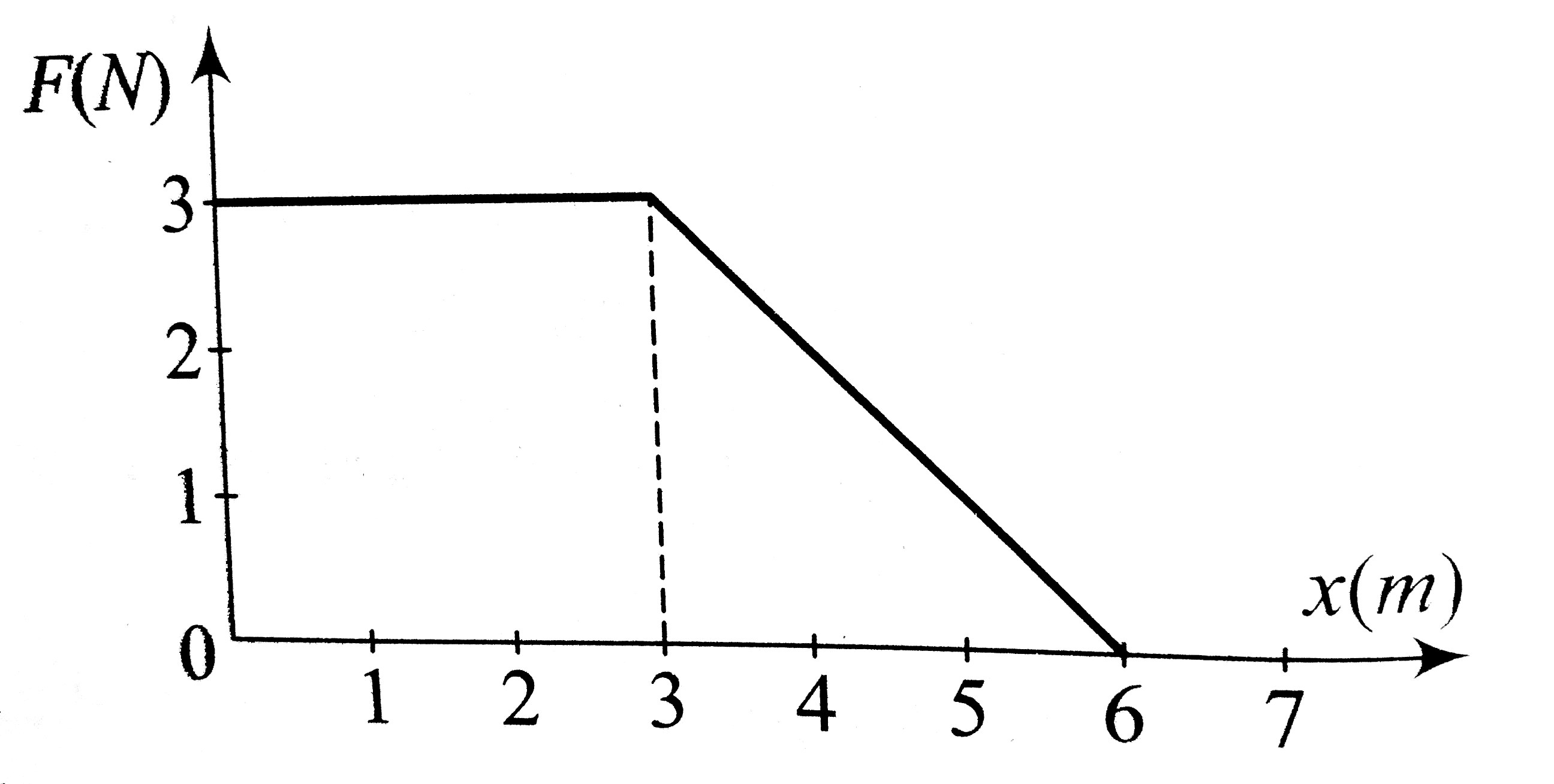 View Solution
View SolutionA particle moves along the x-axis from x=0 to x=5m under the influence of a given by F=7−2x+3x2. The work done by the applied force to the particle is.
View SolutionA force f=10+2x acts on a particle moving in straight line on x axis the work done by this force during a displacement from x=0 and x=3m
View SolutionA force F=(2+x) acts on a particle in x-direction where F is in newton and x in meter. Find the work done by this force during a displacement from 1. 0 m to x = 2.0 m.
View Solution


