A vessel contains oil (density =0.8gm/cm3) over mercury (density =13.6gmcm3). A homogeneous sphere floats with half its volume immersed in mercury and the other half in oil. The density of the material of the sphere in gm/cm3 is
3.3
6.4
7.2
12.8
The correct Answer is:C
To find the density of the material of the sphere, we can follow these steps:
Step 1: Understand the problem
We have a sphere floating in two different liquids: oil and mercury. The sphere is half immersed in oil and half in mercury. We need to find the density of the sphere.
Step 2: Write the equation for the weight of the sphere
The weight of the sphere (W) can be expressed as:
W=V⋅ρ⋅g
where:
- V is the volume of the sphere,
- ρ is the density of the sphere,
- g is the acceleration due to gravity.
Since the sphere is homogeneous, its volume V can be represented as:
V=43πR3
Thus, the weight of the sphere becomes:
W=43πR3⋅ρ⋅g
Step 3: Write the equation for the buoyant force
The buoyant force (upthrust) acting on the sphere is equal to the weight of the liquid displaced by the sphere. Since half of the sphere is immersed in oil and the other half in mercury, we can express the buoyant force (F_b) as:
Fb=Fb,oil+Fb,mercury
where:
- Fb,oil=Volumeoil⋅Densityoil⋅g
- Fb,mercury=Volumemercury⋅Densitymercury⋅g
Since half of the sphere is in each liquid, we have:
Fb,oil=12V⋅ρoil⋅g
Fb,mercury=12V⋅ρmercury⋅g
Thus, the total buoyant force is:
Fb=12V⋅ρoil⋅g+12V⋅ρmercury⋅g
Step 4: Substitute the values
Substituting the values of the densities:
- ρoil=0.8g/cm3
- ρmercury=13.6g/cm3
We get:
Fb=12V⋅0.8⋅g+12V⋅13.6⋅g
Step 5: Set the weight equal to the buoyant force
Since the sphere is floating, the weight of the sphere equals the buoyant force:
43πR3⋅ρ⋅g=12V⋅0.8⋅g+12V⋅13.6⋅g
Step 6: Simplify the equation
We can cancel g and V (since V=43πR3):
ρ=12(0.8+13.6)
Step 7: Calculate the density
Calculating the right side:
ρ=12(0.8+13.6)=12(14.4)=7.2g/cm3
Final Answer
The density of the material of the sphere is:
ρ=7.2g/cm3
---
We have a sphere floating in two different liquids: oil and mercury. The sphere is half immersed in oil and half in mercury. We need to find the density of the sphere.
The weight of the sphere (W) can be expressed as:
W=V⋅ρ⋅g
where:
- V is the volume of the sphere,
- ρ is the density of the sphere,
- g is the acceleration due to gravity.
V=43πR3
Thus, the weight of the sphere becomes:
W=43πR3⋅ρ⋅g
The buoyant force (upthrust) acting on the sphere is equal to the weight of the liquid displaced by the sphere. Since half of the sphere is immersed in oil and the other half in mercury, we can express the buoyant force (F_b) as:
Fb=Fb,oil+Fb,mercury
where:
- Fb,oil=Volumeoil⋅Densityoil⋅g
- Fb,mercury=Volumemercury⋅Densitymercury⋅g
Fb,oil=12V⋅ρoil⋅g
Fb,mercury=12V⋅ρmercury⋅g
Fb=12V⋅ρoil⋅g+12V⋅ρmercury⋅g
Substituting the values of the densities:
- ρoil=0.8g/cm3
- ρmercury=13.6g/cm3
Fb=12V⋅0.8⋅g+12V⋅13.6⋅g
Since the sphere is floating, the weight of the sphere equals the buoyant force:
43πR3⋅ρ⋅g=12V⋅0.8⋅g+12V⋅13.6⋅g
We can cancel g and V (since V=43πR3):
ρ=12(0.8+13.6)
Calculating the right side:
ρ=12(0.8+13.6)=12(14.4)=7.2g/cm3
The density of the material of the sphere is:
ρ=7.2g/cm3
Similar Questions
A piece of iron (density 7.6 g cm−3 ) sinks in mercury (density 13.6g cm−3 ).
View SolutionA sphere is made of an alloy of Metal A (density 8g/cm3) and Metal B (density 6g/cm3). The sphere floats in mercury (density 13.6g/cm3) with half its volume submerged. The percentage of the total volume of the sphere that is occupied by metal A is ___________ .
View Solution
Knowledge Check
A vessel contains oil (density = 0.8 gm/cm2) over mercury (density = 13.6 gm/cm2). A homogeneous sphere floats with half of its volume immersed in mercury and the other half in oil. The density of material of the sphere in gm/cm3 is
A3.3B6.4C7.2D2.8
A hollow spherical body of inner and outer radii 6 cm, and 8 cm respectively floats half submerged in water. Find the density of the material of the sphere.
View SolutionIron has a density of 7.8g/cm3 and mercury has a density of 13.5g/cm3 What happens if an iron nail is put in mercury? Why?
View SolutionA block of wood of volume 30cm3 floats it water with 20cm3 of its volume immersed.
Calculate the density.
View SolutionTwo solids A and B floats in water. It is observed that A floats with half of its volume immersed and B Floats with 2/3 of its volume immersed. The ratio of densities of A and B is
View Solution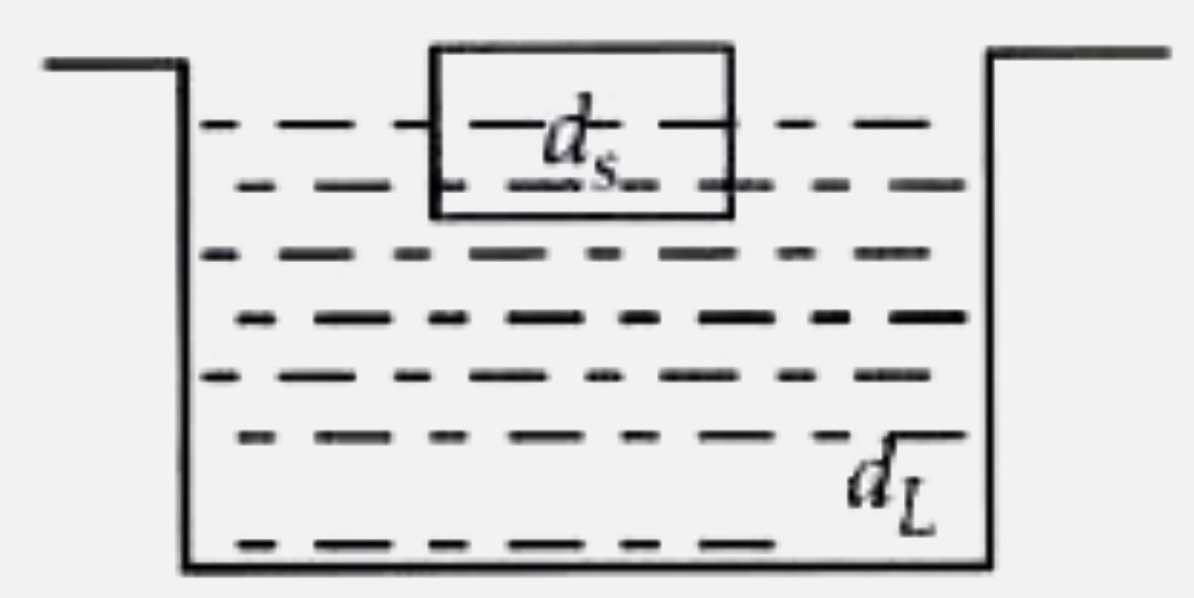
The figure above shows a solid of density dS floating in a liquid of density dL.
The same solid floats in water with 3th5 of its volume immersed in it. Calculate the density of the solid. (density of water = 1 g cm−3 )
View Solution
System is shown in the figure. Velocity of sphere A is 9 ms. Find the speed of sphere B.
View SolutionFind the volume of 900 g of cooking oil whose density is 0.9g/cm3. Give the answer in litres.
View Solution
