Two spherical conductors A and B of radii R and 2R respectively , are separated by a large distance . If some charge is given to both the spheres and later they are connected by a conducting wire , then in equilibrium condition , the ratio of the magnitude of the electric fields at the surface of spheres A and B is
1:4
4:1
1:2
2:1
The correct Answer is:D
To solve the problem, we need to find the ratio of the electric fields at the surfaces of two spherical conductors A and B with radii R and 2R respectively, after they are connected by a conducting wire.
1. Understanding the Problem:
- We have two spherical conductors: Sphere A with radius R and Sphere B with radius 2R.
- Initially, they have charges q1 and q2 respectively.
- When connected by a conducting wire, they will reach an equilibrium state where their electric potentials are equal.
2. Electric Potential of Spheres:
- The electric potential V of a charged sphere is given by:
V=q4πϵ0R
- For Sphere A:
VA=q14πϵ0R
- For Sphere B:
VB=q24πϵ0(2R)=q28πϵ0R
3. Setting the Potentials Equal:
- At equilibrium, VA=VB:
q14πϵ0R=q28πϵ0R
- Simplifying this gives:
2q1=q2
4. Surface Charge Densities:
- The surface charge density σ is given by:
σ=q4πR2
- For Sphere A:
σA=q14πR2
- For Sphere B:
σB=q24π(2R)2=q216πR2
5. Finding the Ratio of Surface Charge Densities:
- Using q2=2q1:
σB=2q116πR2=q18πR2
- Now, the ratio of surface charge densities is:
σAσB=q14πR2q18πR2=84=2
6. Electric Field at the Surface of the Spheres:
- The electric field E at the surface of a charged conductor is given by:
E=σϵ0
- For Sphere A:
EA=σAϵ0
- For Sphere B:
EB=σBϵ0
7. Finding the Ratio of Electric Fields:
- The ratio of the electric fields is:
EAEB=σAσB=2
Conclusion:
The ratio of the magnitudes of the electric fields at the surfaces of spheres A and B is 2:1.
- We have two spherical conductors: Sphere A with radius R and Sphere B with radius 2R.
- Initially, they have charges q1 and q2 respectively.
- When connected by a conducting wire, they will reach an equilibrium state where their electric potentials are equal.
- The electric potential V of a charged sphere is given by:
V=q4πϵ0R
- For Sphere A:
VA=q14πϵ0R
- For Sphere B:
VB=q24πϵ0(2R)=q28πϵ0R
- At equilibrium, VA=VB:
q14πϵ0R=q28πϵ0R
- Simplifying this gives:
2q1=q2
- The surface charge density σ is given by:
σ=q4πR2
- For Sphere A:
σA=q14πR2
- For Sphere B:
σB=q24π(2R)2=q216πR2
- Using q2=2q1:
σB=2q116πR2=q18πR2
- Now, the ratio of surface charge densities is:
σAσB=q14πR2q18πR2=84=2
- The electric field E at the surface of a charged conductor is given by:
E=σϵ0
- For Sphere A:
EA=σAϵ0
- For Sphere B:
EB=σBϵ0
- The ratio of the electric fields is:
EAEB=σAσB=2
The ratio of the magnitudes of the electric fields at the surfaces of spheres A and B is 2:1.
Similar Questions
Two spherical conductors A and B of radii 1mm and 2mm are separated by a distance of 5 cm and are uniformly charged. If the spheres are connected by a conducting wire then in equilibrium condition, the ratio of the magnitude of the electric fields at the surfaces of spheres A and B is
View SolutionTwo metal spheres A and B of radii a & b (a < b) respectively are at a large distance apart. Each sphere carries a charge of 100μO. the sphere are connected by a conducting wire, then
View Solution
Knowledge Check
Two spheres of radius a and b respectively are charged and joined by a wire. The ratio of electric field of the spheres is
AabBbaCa2b2Db2a2
Two spherical conductors of radii R1andR2 are separated by a distance much larger than the radius of eighter sphere. The spheres are connected by a conducting wire as shown in (Fig. 3.128). If the charges on the spheres in equilibrium are q1andq2, respectively, what is the ratio of the field strength at the surfaces of the spheres ?
 .
.
View SolutionThree concentric spherical conductors A, B, and C of radii r, 2R, and 4R, respectively. A and C is shorted and B is uniformly charged (charge +Q).
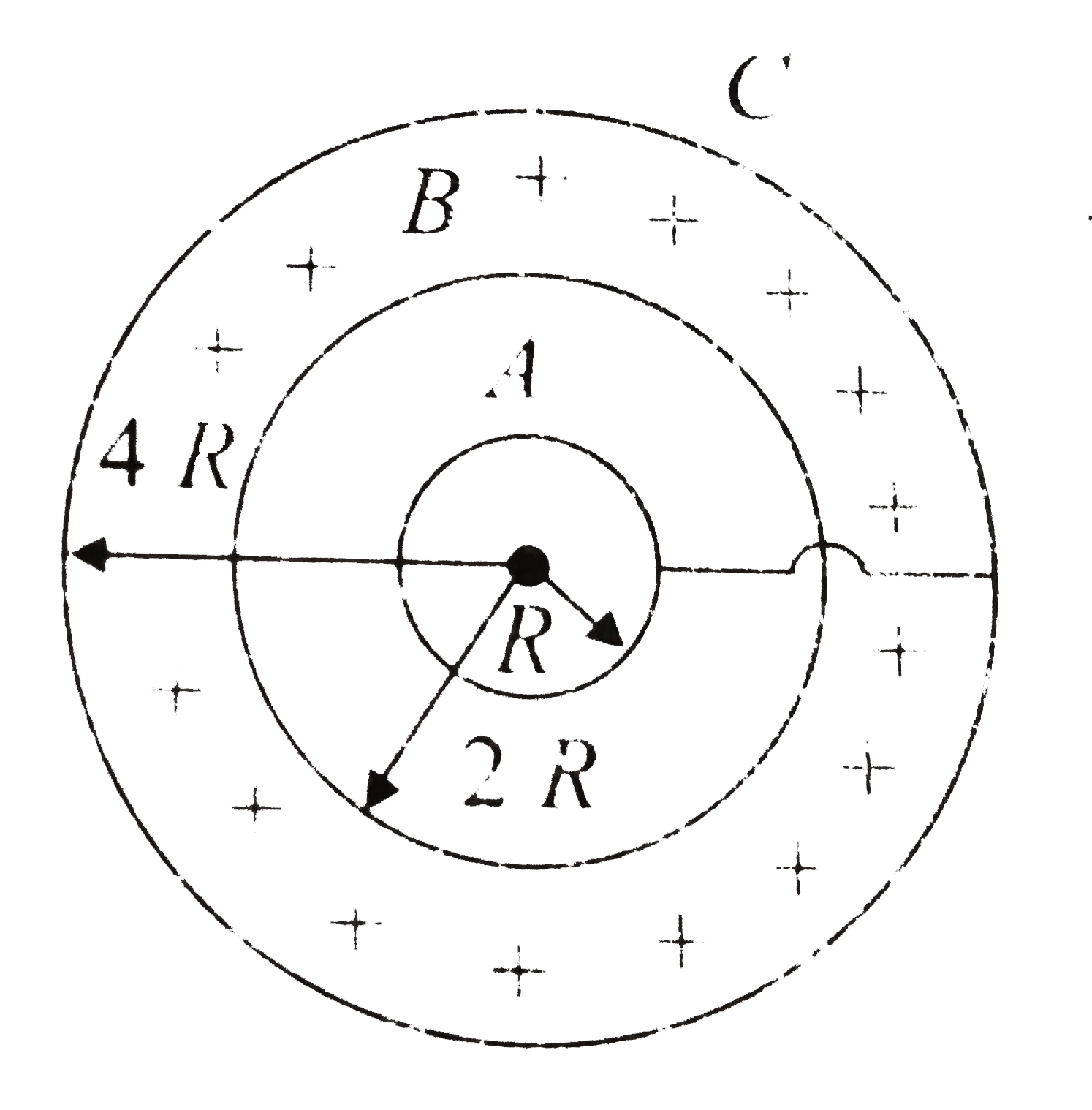
Potential at B is
View SolutionThree concentric spherical conductors A, B, and C of radii r, 2R, and 4R, respectively. A and C is shorted and B is uniformly charged (charge +Q).
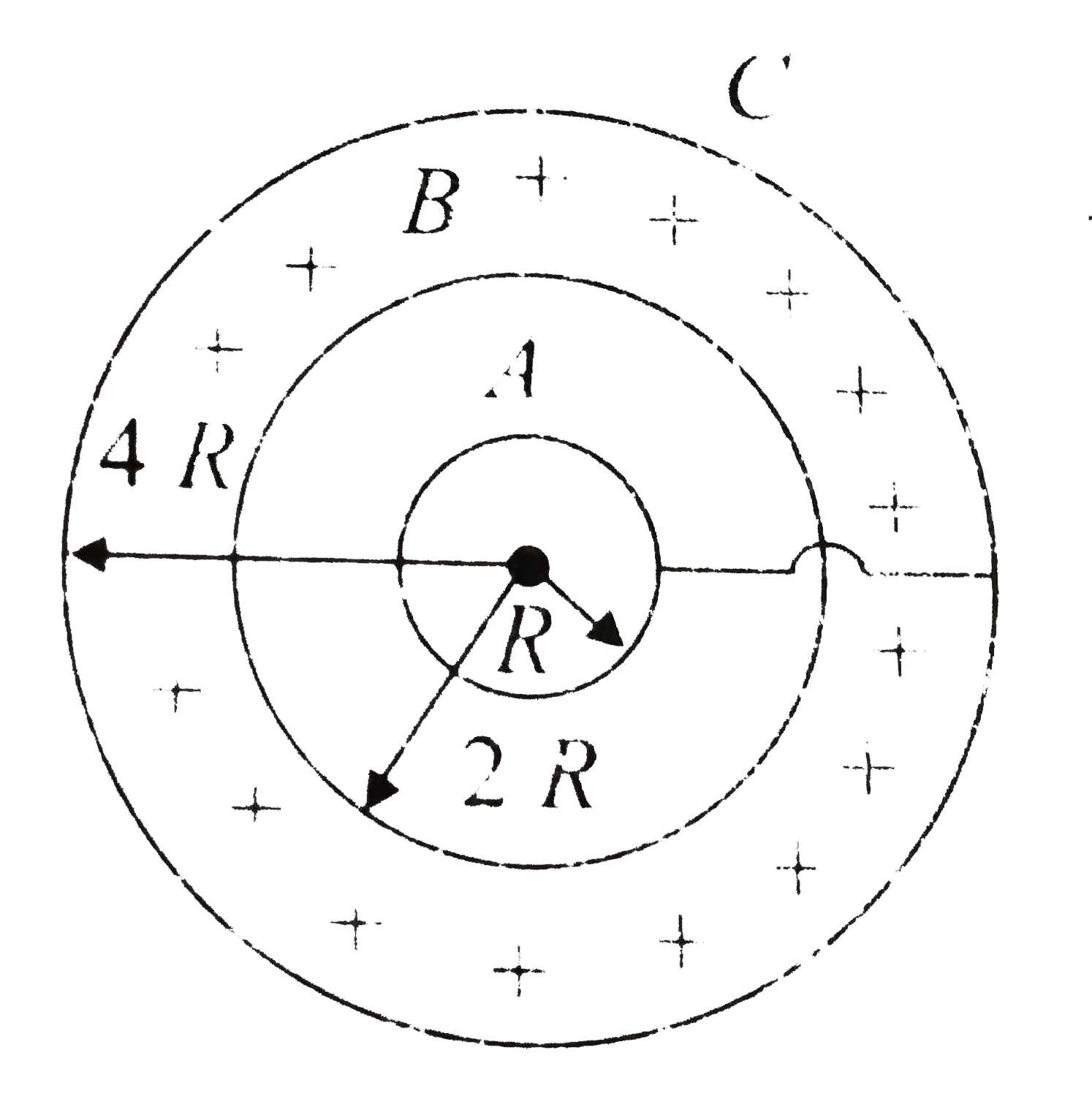
Potential at A is
View SolutionTwo spheres of same metal have radii a and b . They have been connected to a conducting wire. Find the ratio of the electric field intensity upon them.
View SolutionTwo spheres A and B of radius 'a' and 'b' respectively are at same electric potential. The ratio of the surface charge densities of A and B is
View SolutionThree concentric spherical conductors A, B, and C of radii r, 2R, and 4R, respectively. A and C is shorted and B is uniformly charged (charge +Q).
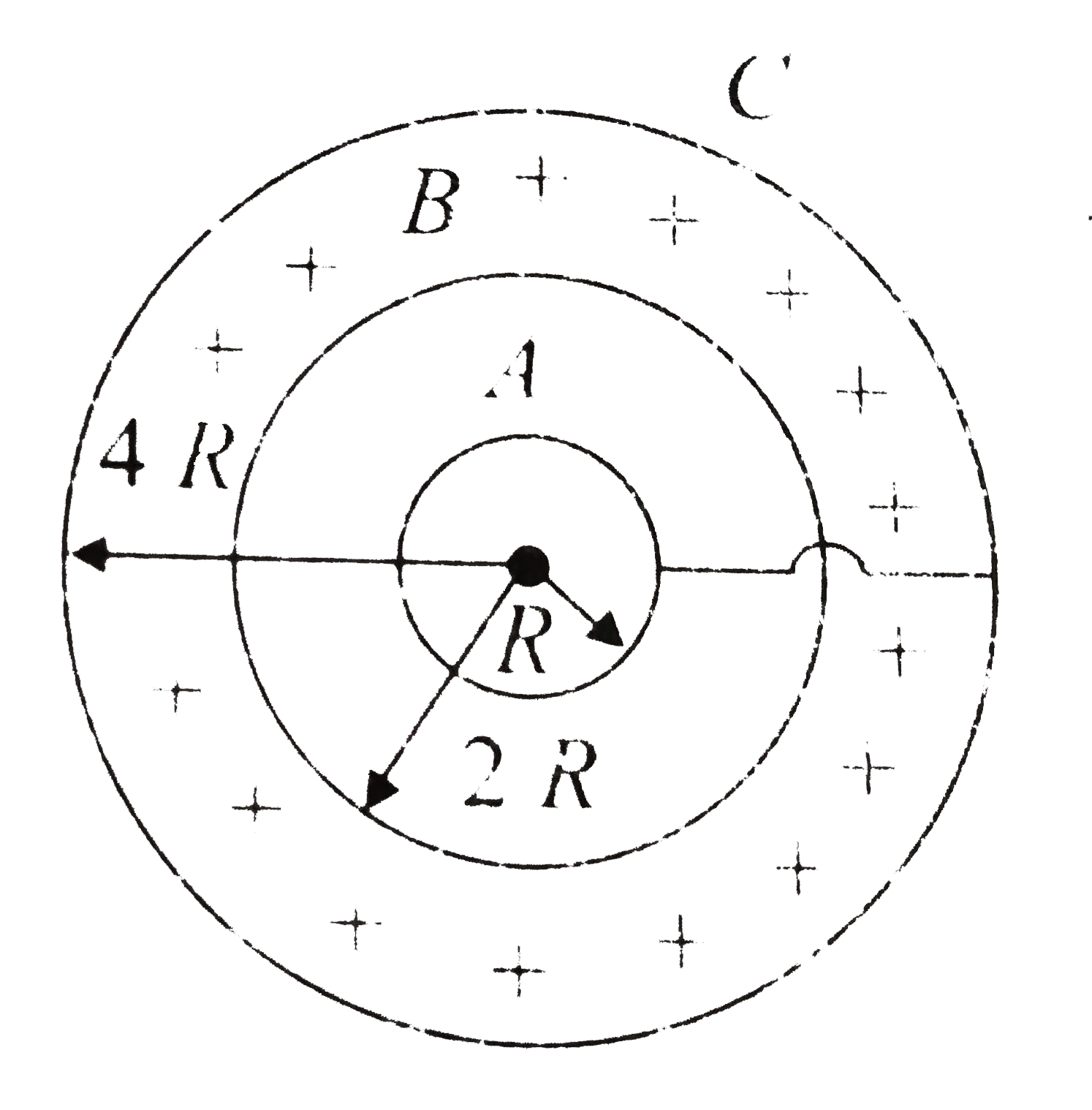
Charge on conductor A is
View SolutionTwo concentric spherical conducting shells of radii R and 2R carry charges Q and 2Qrespectively.Change in electric potential on the outer shell when both are connected by a conducting wire is (k=14πɛ0)
View Solution