Two spherical conductors A and B of radii 1mm and 2mm are separated by a distance of 5 cm and are uniformly charged. If the spheres are connected by a conducting wire then in equilibrium condition, the ratio of the magnitude of the electric fields at the surfaces of spheres A and B is
4:1
1:2
2:1
1:4
The correct Answer is:A
To solve the problem step by step, we will analyze the situation involving two spherical conductors A and B, their radii, and the electric fields at their surfaces.
Step 1: Understand the Problem
We have two spherical conductors:
- Sphere A with radius r1=1mm=0.001m
- Sphere B with radius r2=2mm=0.002m
They are separated by a distance of d=5cm=0.05m. When connected by a conducting wire, they will reach an equilibrium state where their potentials are equal.
Step 2: Set Up the Equations
When the spheres are connected by a wire, the potentials VA and VB will be equal:
VA=VB
The potential V of a charged sphere is given by:
V=kQr
where k is Coulomb's constant, Q is the charge, and r is the radius of the sphere.
Thus, we can write:
kQ1r1=kQ2r2
Step 3: Simplify the Equation
Since k is a constant, it cancels out:
Q1r1=Q2r2
This can be rearranged to give us the ratio of the charges:
Q1Q2=r1r2
Step 4: Calculate the Electric Fields
The electric field E at the surface of a charged sphere is given by:
E=kQr2
For spheres A and B, we have:
EA=kQ1r21
EB=kQ2r22
Step 5: Find the Ratio of Electric Fields
We want to find the ratio EAEB:
EAEB=kQ1r21kQ2r22=Q1Q2⋅r22r21
Substituting the ratio of charges from Step 3:
EAEB=r1r2⋅r22r21
Step 6: Simplify the Expression
This simplifies to:
EAEB=r2r1
Step 7: Substitute the Values
Now substituting the values of r1 and r2:
EAEB=2mm1mm=2
Final Answer
Thus, the ratio of the magnitude of the electric fields at the surfaces of spheres A and B is:
EAEB=2:1
We have two spherical conductors:
- Sphere A with radius r1=1mm=0.001m
- Sphere B with radius r2=2mm=0.002m
When the spheres are connected by a wire, the potentials VA and VB will be equal:
VA=VB
V=kQr
where k is Coulomb's constant, Q is the charge, and r is the radius of the sphere.
kQ1r1=kQ2r2
Since k is a constant, it cancels out:
Q1r1=Q2r2
This can be rearranged to give us the ratio of the charges:
Q1Q2=r1r2
The electric field E at the surface of a charged sphere is given by:
E=kQr2
EA=kQ1r21
EB=kQ2r22
We want to find the ratio EAEB:
EAEB=kQ1r21kQ2r22=Q1Q2⋅r22r21
EAEB=r1r2⋅r22r21
This simplifies to:
EAEB=r2r1
Now substituting the values of r1 and r2:
EAEB=2mm1mm=2
Thus, the ratio of the magnitude of the electric fields at the surfaces of spheres A and B is:
EAEB=2:1
Similar Questions
Two spherical conductors A and B of radii R and 2R respectively , are separated by a large distance . If some charge is given to both the spheres and later they are connected by a conducting wire , then in equilibrium condition , the ratio of the magnitude of the electric fields at the surface of spheres A and B is
View SolutionTwo metal spheres A and B of radii a & b (a < b) respectively are at a large distance apart. Each sphere carries a charge of 100μO. the sphere are connected by a conducting wire, then
View SolutionTwo spherical conductors of radii R1andR2 are separated by a distance much larger than the radius of eighter sphere. The spheres are connected by a conducting wire as shown in (Fig. 3.128). If the charges on the spheres in equilibrium are q1andq2, respectively, what is the ratio of the field strength at the surfaces of the spheres ?
 .
.
View SolutionTwo conducting spheres of radii 3 cm and 1 m are separated by a distance of 10 cm in free space. If the spheres are charged to same potential of 10 V each, then the force of repulsion between them is
View SolutionThree concentric spherical conductors A, B, and C of radii r, 2R, and 4R, respectively. A and C is shorted and B is uniformly charged (charge +Q).
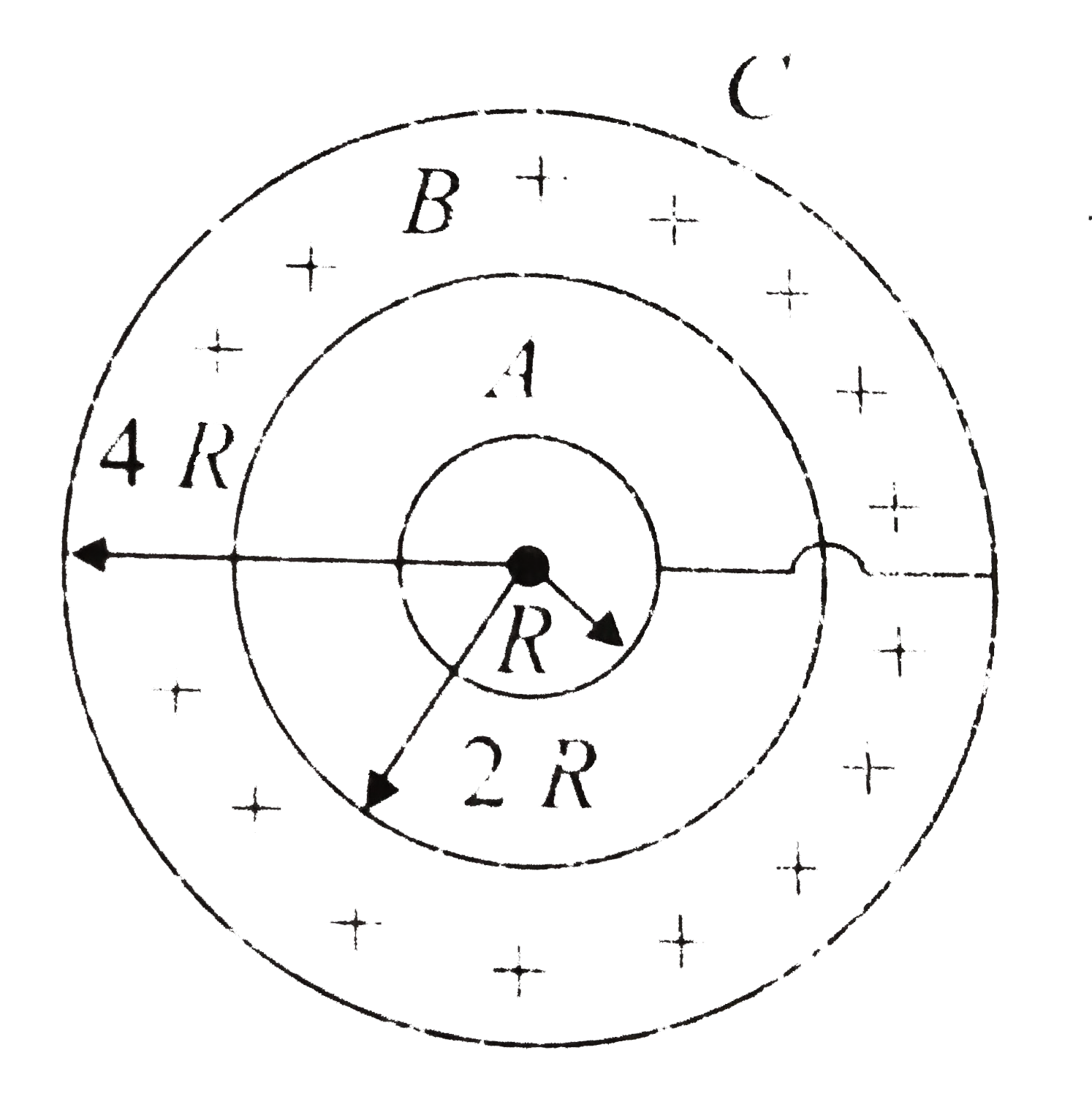
Charge on conductor A is
View SolutionTwo concentric spherical conducting shells of radii R and 2R are carrying charges q and 2q, respectively. Both are now connected by a conducting wire. Find the change in electric potential (inV) on the outer shell.
View SolutionTwo spherical conductor A and B of radii a and b (b>a) are placed concentrically in air. The two are connected by a copper wire as shown in figure. The equivalent capacitance of the system is

View SolutionTwo conducting spheres of radii r and 2r are placed at very large separation. Each sphere possesses charge Q. These spheres are connected with a conducting wire of resistance R. Then, which of the following is true?
View SolutionFigure shows two conducting spheres separated by large distance and of radius 2 cm and 3 cm containing charges 10μC and 20μC respectively. When the spheres are connected by a conducting wire then find out following :
(i) Ratio of the final charge.
(ii) Final charge on each sphere.
(iii) Ratio of final charge densities.
(iv) Heat produced during the process.

View SolutionTwo spheres of same metal have radii a and b . They have been connected to a conducting wire. Find the ratio of the electric field intensity upon them.
View Solution