n identical cells are joined in series with two cells A and B with reversed polarities. EMF of each cell is E and internal resistance is r. Potential difference across cell A or B is (n gt 4)
2En
2E(1−(1)n)
4En
2E(1−2n)
The correct Answer is:D
To solve the problem of finding the potential difference across cell A or B when n identical cells are joined in series with two cells A and B of reversed polarities, we can follow these steps:
Step 1: Understand the Configuration
We have n identical cells, each with an EMF \( E \) and internal resistance \( r \). These cells are connected in series with two additional cells A and B, which are connected in reverse polarity.
Step 2: Calculate the Total EMF
When cells are connected in series, the total EMF is the sum of the individual EMFs. However, since cells A and B are connected in reverse polarity, they will subtract from the total EMF contributed by the other cells.
The total EMF contributed by the n cells is:
\(
E_{\text{total}} = nE
\)
Since cells A and B are in reverse polarity, we subtract their EMFs:
\(
E_{\text{equivalent}} = nE - 2E = (n - 2)E
\)
Step 3: Calculate the Total Internal Resistance
The internal resistance of each cell is \( r \). Since all cells are in series, the total internal resistance \( R_{\text{total}} \) is:
\(
R_{\text{total}} = nr + r + r = nr + 2r = (n + 2)r
\)
Step 4: Calculate the Current in the Circuit
Using Ohm's law, the current \( I \) in the circuit can be calculated using the equivalent EMF and total internal resistance:
\(
I = \frac{E_{\text{equivalent}}}{R_{\text{total}}} = \frac{(n - 2)E}{(n + 2)r}
\)
Step 5: Calculate the Potential Difference Across Cells A and B
The potential difference \( V \) across cells A and B can be calculated using the formula:
\(
V = E_{\text{equivalent}} - I \cdot R_{\text{total}}
\)
Substituting the values we have:
\(
V = (n - 2)E - \left(\frac{(n - 2)E}{(n + 2)r}\right) \cdot (n + 2)r
\)
The \( r \) cancels out:
\(
V = (n - 2)E - (n - 2)E = 0
\)
However, we need to find the potential difference specifically across cells A and B. Since cells A and B are in reverse polarity, the potential difference across them can be expressed as:
\(
\Delta V = 4E/n
\)
Final Answer
The potential difference across cell A or B is:
\(
\Delta V = \frac{4E}{n}
\)
We have n identical cells, each with an EMF \( E \) and internal resistance \( r \). These cells are connected in series with two additional cells A and B, which are connected in reverse polarity.
When cells are connected in series, the total EMF is the sum of the individual EMFs. However, since cells A and B are connected in reverse polarity, they will subtract from the total EMF contributed by the other cells.
\(
E_{\text{total}} = nE
\)
Since cells A and B are in reverse polarity, we subtract their EMFs:
\(
E_{\text{equivalent}} = nE - 2E = (n - 2)E
\)
The internal resistance of each cell is \( r \). Since all cells are in series, the total internal resistance \( R_{\text{total}} \) is:
\(
R_{\text{total}} = nr + r + r = nr + 2r = (n + 2)r
\)
Using Ohm's law, the current \( I \) in the circuit can be calculated using the equivalent EMF and total internal resistance:
\(
I = \frac{E_{\text{equivalent}}}{R_{\text{total}}} = \frac{(n - 2)E}{(n + 2)r}
\)
The potential difference \( V \) across cells A and B can be calculated using the formula:
\(
V = E_{\text{equivalent}} - I \cdot R_{\text{total}}
\)
Substituting the values we have:
\(
V = (n - 2)E - \left(\frac{(n - 2)E}{(n + 2)r}\right) \cdot (n + 2)r
\)
The \( r \) cancels out:
\(
V = (n - 2)E - (n - 2)E = 0
\)
\(
\Delta V = 4E/n
\)
The potential difference across cell A or B is:
\(
\Delta V = \frac{4E}{n}
\)
Similar Questions
n identical cells are joined in series with two cells A and B with reversed polarities. EMF of each cell is E and internal resistance is r. Potential difference across cell A or B is (n > 4)
View SolutionA capacitor is conneted to a cell emf E having some internal resistance r. The potential difference across the
View Solution
Knowledge Check
Two cells e1ande2 connected in opposition to each other as shown in figure. The cell of emf 9 V and internal resistance 3Ω the cell is of emf 7V and internal resistance 7Ω. The potential difference between the points A and B is
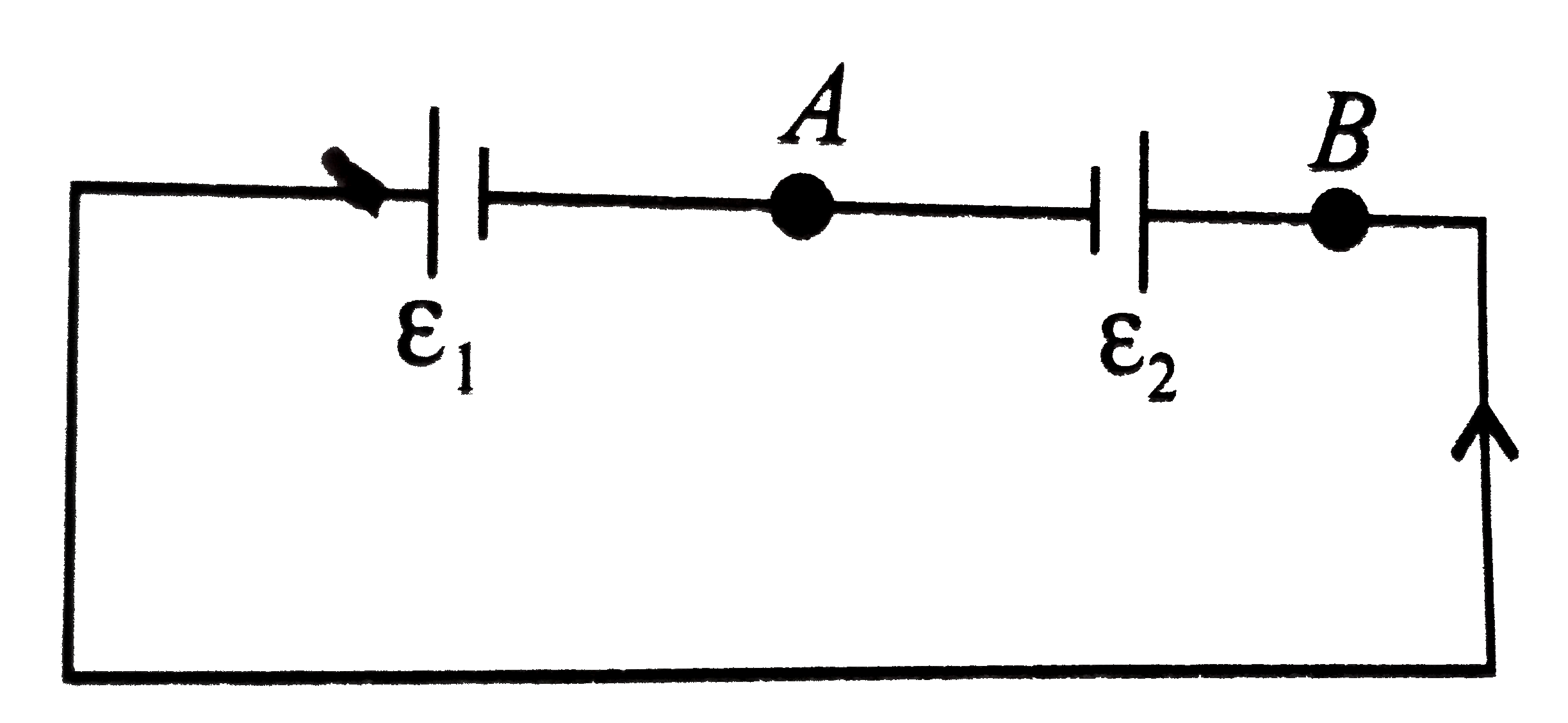 A8.4VB5.6VC7.8VD6.6V
A8.4VB5.6VC7.8VD6.6V
If E is the emf of a cell of internal resistance r and external resistance R, then potential difference across R is given as
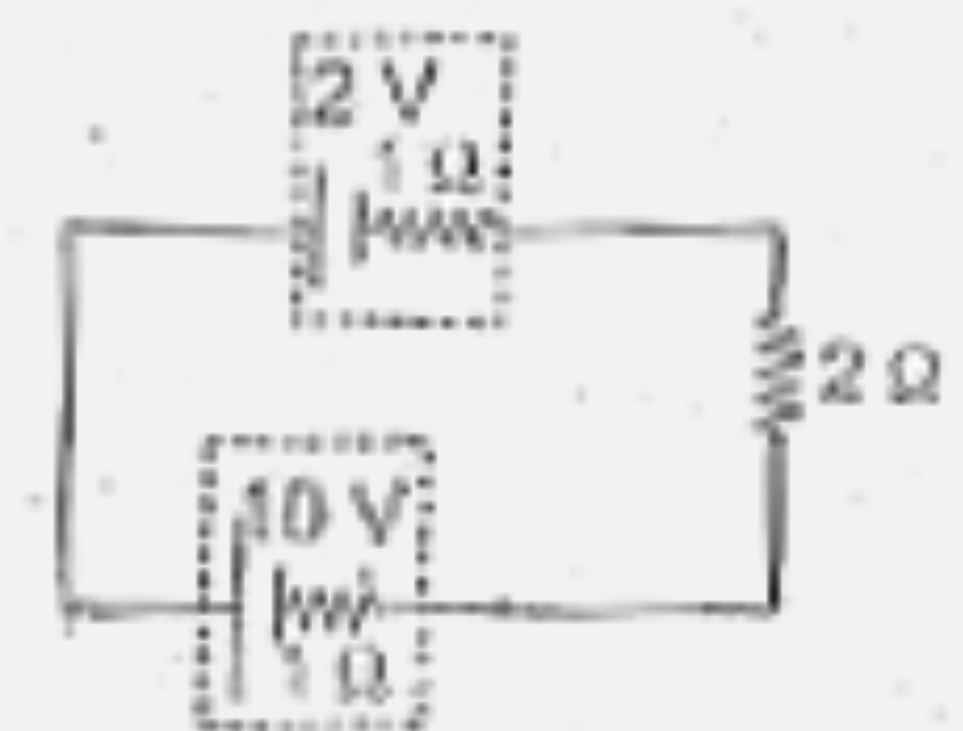
View SolutionIn the situation shown , The potential difference across the cell of smaller e.m.f. is

View SolutionIn the situation shown , the potential difference across the cell of smaller e.m.f is .
View SolutionN identical cells whether joined together in series or in parallel, give the same current, when connected to an external resistance of 'R'. The internal resistance of each cell is:-
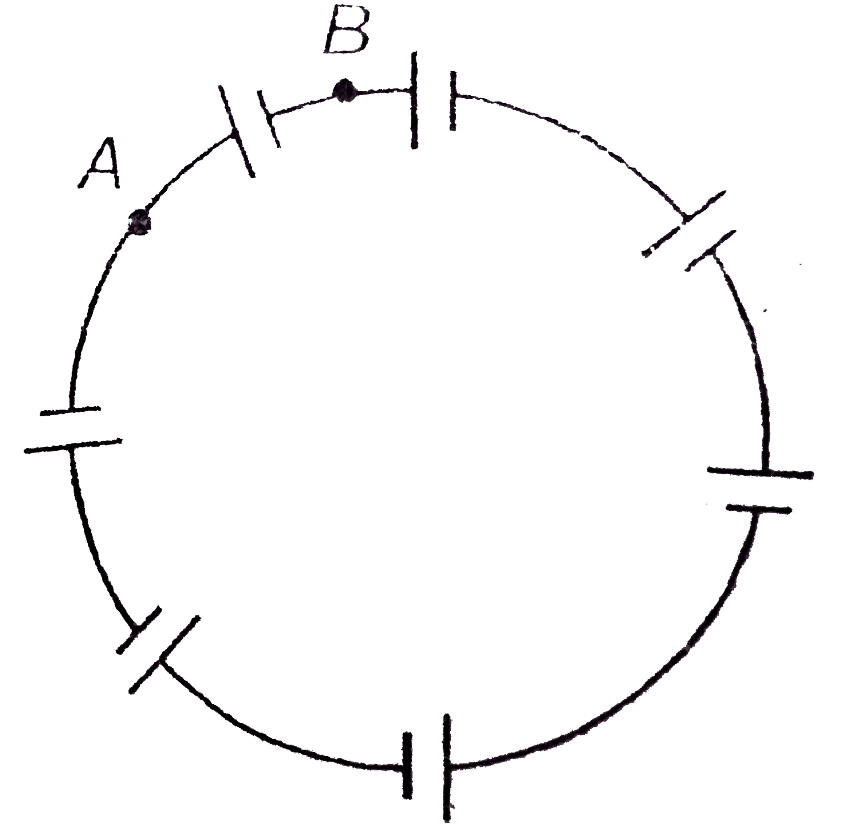
View SolutionSeven identical cells each of e.m.f. E and internal resistance r are connected as shown . The potential difference between A and B is
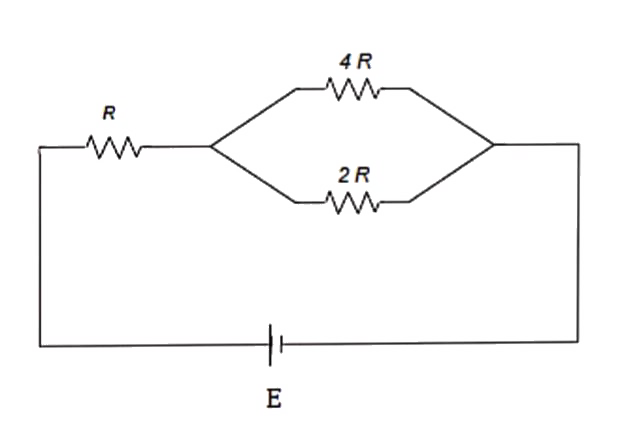
View SolutionThe figure shows a network in which the cell is deal and it has an emf E. The potential difference across the resistance 2R is
View SolutionFour cells each of emf E and internal resistance r are connected in series to form a loop ABCD. Find potential difference across (1) AB, (2) AC
View Solution
