A uniform metal rod is moving with a uniform velocity v parallel to a long straight wire carrying a current I. The rod is perpendicular to the wire with its ends at distance r1andr2 (with r2>r1) form it. The E.M.F. induced in the rod at that instant is
zero
μ0Iv2πln(r2r1)
μ0Iv2πln(r1r2)
μ0Iv4π(1−r1r2)
The correct Answer is:B
To find the EMF induced in the uniform metal rod moving with a uniform velocity v parallel to a long straight wire carrying a current I, we can follow these steps:
Step 1: Understand the magnetic field around the wire
The magnetic field B at a distance r from a long straight wire carrying current I is given by the formula:
B=μ0I2πr
where μ0 is the permeability of free space.
Step 2: Consider a small element of the rod
Let’s consider a small element of the rod of length dx at a distance x from the wire. The magnetic field at this point is:
B(x)=μ0I2πx
Step 3: Calculate the induced EMF in the small element
The induced EMF dE in the small element dx moving with velocity v is given by:
dE=B⋅v⋅dx
Substituting the expression for B:
dE=(μ0I2πx)vdx
Step 4: Integrate to find the total EMF
To find the total EMF E induced in the entire rod, we need to integrate dE from r1 to r2:
E=∫r2r1dE=∫r2r1(μ0Iv2πx)dx
This integral can be simplified:
E=μ0Iv2π∫r2r11xdx
Step 5: Solve the integral
The integral of 1x is lnx:
E=μ0Iv2π(lnx)r2r1
This evaluates to:
E=μ0Iv2π(lnr2−lnr1)
Using the properties of logarithms, we can write this as:
E=μ0Iv2πln(r2r1)
Final Answer
Thus, the EMF induced in the rod is:
E=μ0Iv2πln(r2r1)
---
The magnetic field B at a distance r from a long straight wire carrying current I is given by the formula:
B=μ0I2πr
where μ0 is the permeability of free space.
Let’s consider a small element of the rod of length dx at a distance x from the wire. The magnetic field at this point is:
B(x)=μ0I2πx
The induced EMF dE in the small element dx moving with velocity v is given by:
dE=B⋅v⋅dx
Substituting the expression for B:
dE=(μ0I2πx)vdx
To find the total EMF E induced in the entire rod, we need to integrate dE from r1 to r2:
E=∫r2r1dE=∫r2r1(μ0Iv2πx)dx
This integral can be simplified:
E=μ0Iv2π∫r2r11xdx
The integral of 1x is lnx:
E=μ0Iv2π(lnx)r2r1
This evaluates to:
E=μ0Iv2π(lnr2−lnr1)
Using the properties of logarithms, we can write this as:
E=μ0Iv2πln(r2r1)
Thus, the EMF induced in the rod is:
E=μ0Iv2πln(r2r1)
Similar Questions
A copper rod of length 0.19m is moving with uniform velocity 10ms−1 parallel to a long straight wire carrying a current of 5.0A. The rod is perpendicular to the wire with its ends at distances 0.01 and 0.2m from it. Calculate the emf induced in the rod.
View SolutionA copper rod moves with a constant angular velocity ω about a long straight wire carrying a current I. If the ends of the rod from the wire are at distances a and b, then the e.m.f induced in the rod is
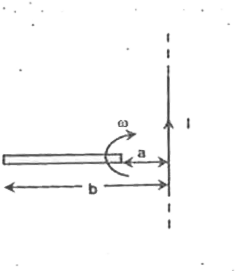
View SolutionShows a copper rod moving with velocity v parallel to a long straight wire carrying current =100A. Calculate the induced emf in the rod, where v=5mS−1, a=1cm , b=100cm.
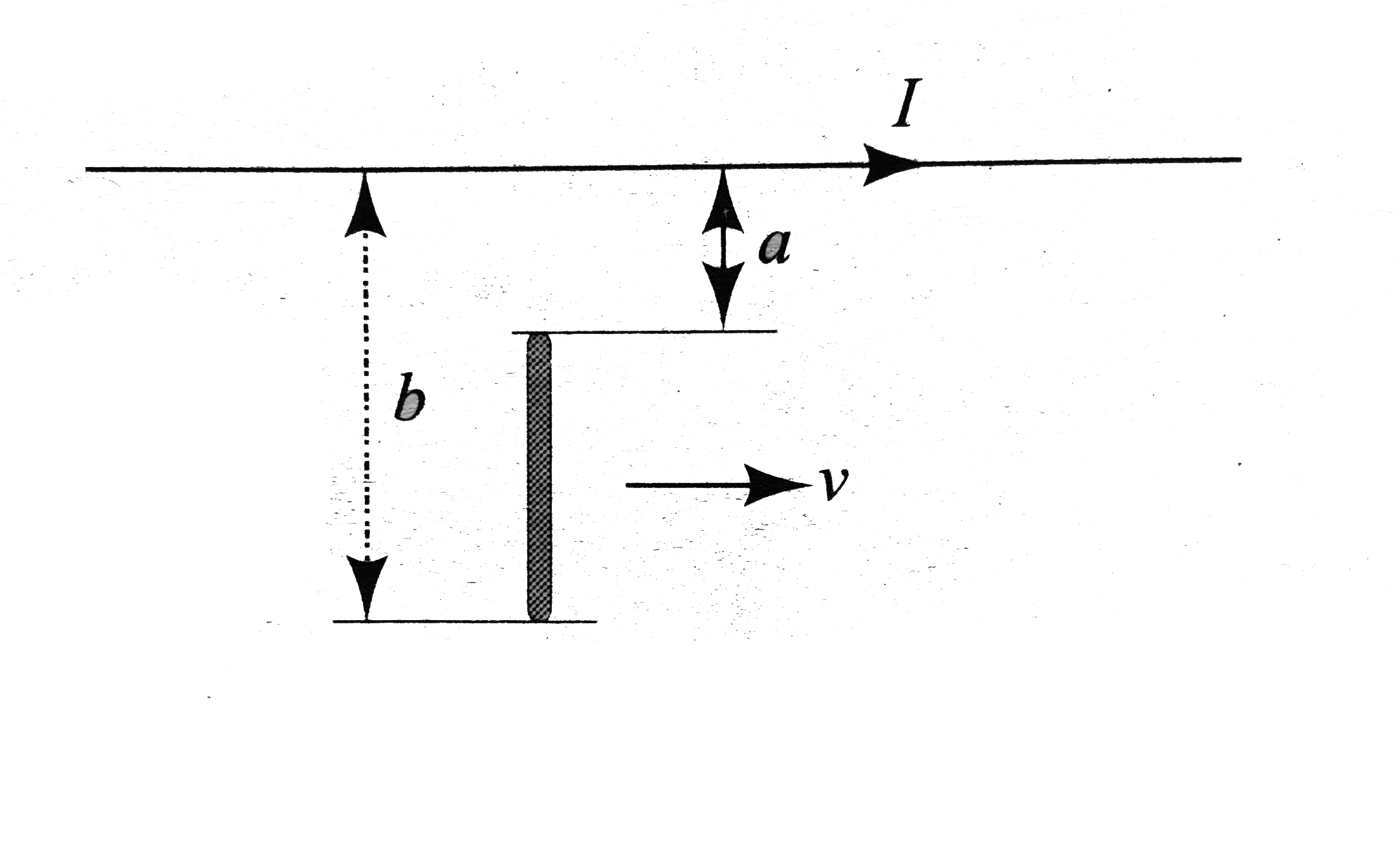
View SolutionThe figure shows a copper rod moving with velocity v parallel to a long straight wire carrying a current I = 100 A. Calculate the induced emf in the rod, assuming that v = 5 m/s, a = 1 cm and b = 100 cm.
View SolutionA conducting circular loop of radius a and resistance per unit length R is moving with a constant velocity v0 , parallel to an infinite conducting wire carrying current i0. A conducting rod of length 2a is approaching the centre of the loop with a constant velocity v02 along the direction 2 of the current. At the instant t=0, the rod comes in contact with the loop at A and starts sliding on the loop with the constant velocity. Neglecting the resistance of the rod and the self-inductance of the circuit, find the following when the rod slides on the loop.

(a) The current through the rod when it is at a distance of (a2) from the point A of the loop.
(b) Force required to maintain the velocity of the rod at that instant.
View SolutionA rod of length l is placed perpendicular to a long wire carrying current i. The rod is moved parallel to the wire with a velocity v. Find the emf induced in the rod, if its nearest end is at a distance a from the wire.

View SolutionA rod of length l is placed perpendicular to a long wire carrying current i. The rod is moved parallel to the wire with a velocity v. Find the emf induced in the rod, if its nearest end is at a distance a from the wire.

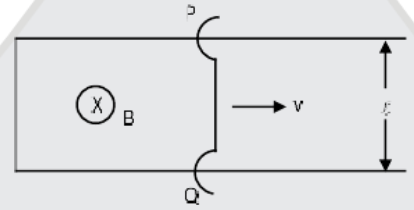
View SolutionA rod having length l and resistance R is moving with velocity v on a π shape conductor. Find the current in the rod.
View SolutionA rod of length l is kept parallel to a long wire carrying constant current i . It is moving away from the wire with a velocity v. Find the emf induced in the wire when its distance from the long wire is x.
View SolutionA square loop of side a is placed in the same plane as a long straight wire carrying a current i. The centre of the loop is at a distance r from wire where r>>a. The loop is moved away from the wire with a constant velocity v. The induced e.m.f in the loop is
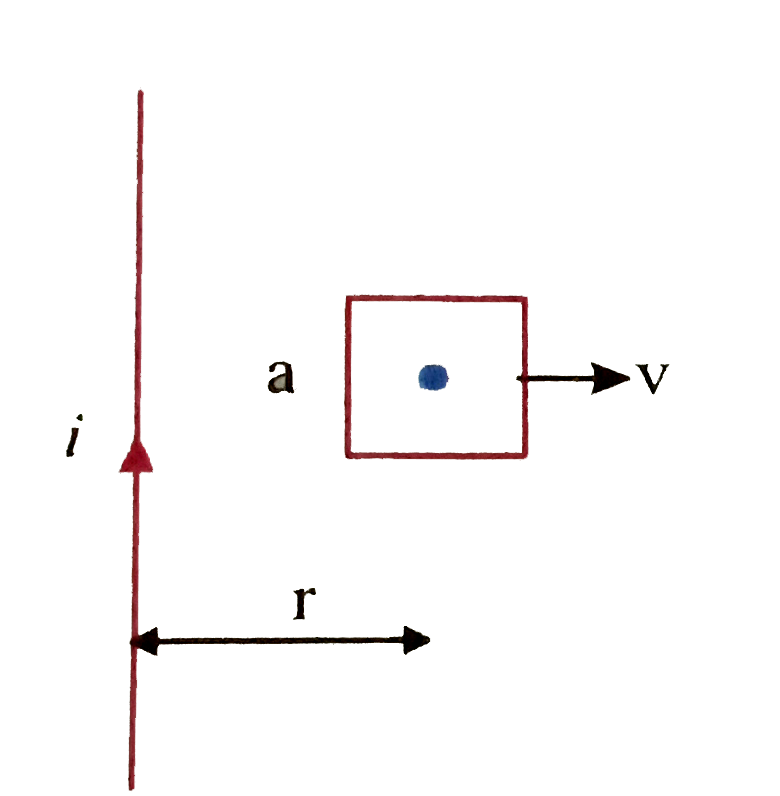
View Solution

