A long solenoid of cross-sectional radius a has a thin insulates wiere ring tightly put on its winding, one half of the ring has the resistance η times that of the other half. The magneticv induction produced by the solenoid varies with the time as B=bt, where b is a constant. Find the magnitude of the electric field strength in the ring.
911Rb
922Rb
9Rb
Rb
The correct Answer is:B
To solve the problem, we need to find the magnitude of the electric field strength in the wire ring surrounding the solenoid. The solenoid produces a changing magnetic field, which induces an electromotive force (emf) in the ring according to Faraday's law of electromagnetic induction.
1. Identify the Magnetic Field:
The magnetic induction (B) produced by the solenoid varies with time as B=bt, where b is a constant.
2. Apply Faraday's Law:
According to Faraday's law, the induced emf (E) in the ring is given by:
E=−dΦBdt
where ΦB is the magnetic flux through the ring.
3. Calculate the Magnetic Flux:
The magnetic flux ΦB through the ring is given by:
ΦB=B⋅A=B⋅πa2
where A is the area of the ring, and a is the radius of the cross-section of the solenoid.
4. Differentiate the Magnetic Flux:
Since B=bt, we have:
ΦB=(bt)⋅πa2
Now, differentiate ΦB with respect to time t:
dΦBdt=πa2b
5. Calculate the Induced EMF:
Substitute the expression for dΦBdt into Faraday's law:
E=−dΦBdt=−πa2b
6. Determine the Current in the Ring:
The ring has two halves with different resistances. Let the resistance of one half be R1=ηR and the other half R2=R. The total resistance Rtotal is:
Rtotal=R1+R2=ηR+R=(η+1)R
7. Calculate the Current:
Using Ohm's law, the current I in the ring can be calculated as:
I=ERtotal=−πa2b(η+1)R
8. Find the Electric Field Strength:
The electric field E in the ring can be found using the relationship between the electric field and the current:
E=EL
where L is the circumference of the ring, L=2πa. Thus:
E=−πa2b(η+1)R⋅2πa=−ab2(η+1)R
Final Result:
The magnitude of the electric field strength in the ring is:
E=ab2(η+1)R
The magnetic induction (B) produced by the solenoid varies with time as B=bt, where b is a constant.
According to Faraday's law, the induced emf (E) in the ring is given by:
E=−dΦBdt
where ΦB is the magnetic flux through the ring.
The magnetic flux ΦB through the ring is given by:
ΦB=B⋅A=B⋅πa2
where A is the area of the ring, and a is the radius of the cross-section of the solenoid.
Since B=bt, we have:
ΦB=(bt)⋅πa2
Now, differentiate ΦB with respect to time t:
dΦBdt=πa2b
Substitute the expression for dΦBdt into Faraday's law:
E=−dΦBdt=−πa2b
The ring has two halves with different resistances. Let the resistance of one half be R1=ηR and the other half R2=R. The total resistance Rtotal is:
Rtotal=R1+R2=ηR+R=(η+1)R
Using Ohm's law, the current I in the ring can be calculated as:
I=ERtotal=−πa2b(η+1)R
The electric field E in the ring can be found using the relationship between the electric field and the current:
E=EL
where L is the circumference of the ring, L=2πa. Thus:
E=−πa2b(η+1)R⋅2πa=−ab2(η+1)R
The magnitude of the electric field strength in the ring is:
E=ab2(η+1)R
Similar Questions
A long solenoid has 800 turns per metre length of solenoid A currentof 1.6 A flow through it. The magnetic induction at the end of the solenoid on its axis is
View SolutionThe magnetic induction at the centre of a solenoid is B. If the length of the solenoid is reduced to half and the same wire is would in two layers the new magnetic induction is
View Solution
Knowledge Check
A 90 cm long solenoid has six layers of windings of 450 turns each. If the diameter of solenoid is 2.2 cm and current carried is 6 A, then the magnitude of magnetic field inside the solenoid, near its centre is
A50πGB60πGC72πGD80πG
Charge q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
View SolutionA conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
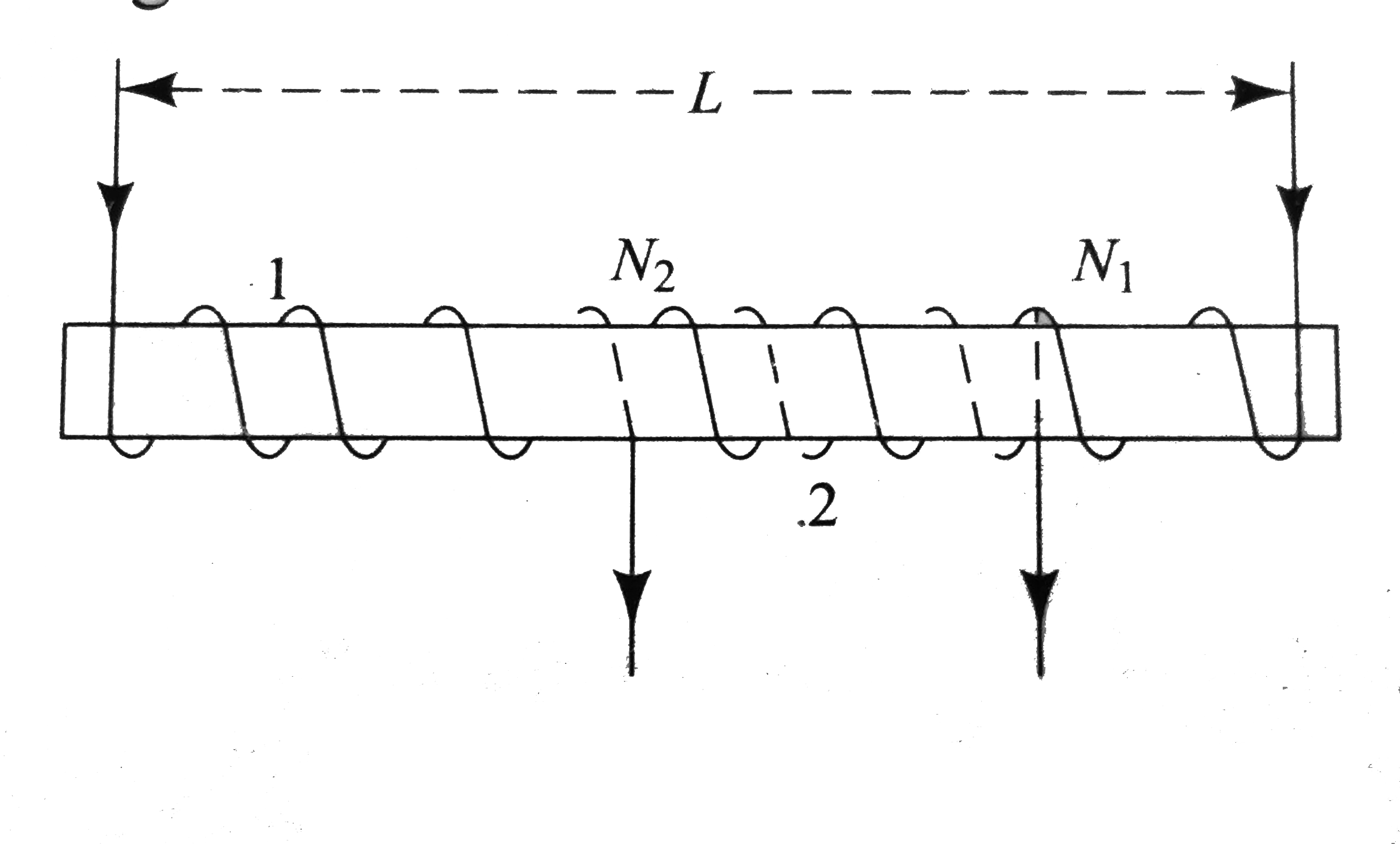
View SolutionA long solenoid of length L, cross section A having N1 turns has about its center a small coil of N2 turns as shows in Fig The mutual inductance of two circuits is
View SolutionA half ring of radius r has a linear charge density λ.The potential at the centre of the half ring is
View SolutionA conductor of length l has a non-uniform cross-section. The radius of cross-section varies linearly from a to b. The resistivity of the material is ρ. Find the resistance of the conductc across its ends.

View SolutionA solenoid is 1.5 m long and its inner diameter is 4.0 cm . It has three layers of windings of 1000 turns each and carries a current of 2.0 amperes. The magnetic flux for a cross-section of the solenoid is nearly
View SolutionA solenoid of length 20cm, area of cross- section 4.0cm2 and having 4000 turns is placed inside another solenoid of 2000 turns having a cross - sectional area 8.0cm2 and length 10cm. Find the mutual inductance between the solenoids.
View Solution
