In balanced meter bridge, the resistance of bridge wire is 0.1Ωcm . Unknown resistance X is connected in left gap and 6Ω in right gap, null point divides the wire in the ratio 2:3 . Find the current drawn the battery of 5V having negligible resistance
The correct Answer is:1
To solve the problem step by step, we will follow these steps:
Step 1: Calculate the total resistance of the bridge wire
The resistance of the bridge wire is given as 0.1Ω/cm and the length of the wire is 100cm.
Total resistance of the wire=Resistance per cm×Length=0.1Ω/cm×100cm=10Ω
Step 2: Understand the ratio in which the wire is divided
The null point divides the wire in the ratio 2:3. This means that the left segment of the wire (where the unknown resistance X is connected) is 2 parts, and the right segment (where 6Ω is connected) is 3 parts.
Let the total length of the wire be L=100cm.
- Length of left segment = 22+3×100cm=25×100cm=40cm
- Length of right segment = 32+3×100cm=35×100cm=60cm
Step 3: Calculate the resistance of each segment of the wire
Using the resistance per cm, we can calculate the resistance of each segment:
- Resistance of left segment (40 cm):
R1=0.1Ω/cm×40cm=4Ω
- Resistance of right segment (60 cm):
R2=0.1Ω/cm×60cm=6Ω
Step 4: Apply the Wheatstone bridge condition
In a balanced meter bridge, the ratio of the resistances is given by:
X6=R1R2=46
From this, we can find the unknown resistance X:
X=6×46=4Ω
Step 5: Calculate the equivalent resistance of the circuit
Now we have:
- Resistance X=4Ω
- Resistance of the wire segments: R1=4Ω and R2=6Ω
The total resistance in the circuit is the sum of the resistances in series:
Rtotal=R1+R2=4Ω+6Ω=10Ω
Step 6: Calculate the current drawn from the battery
Using Ohm's law, the current I drawn from the battery can be calculated as:
I=VRtotal=5V10Ω=0.5A
Final Answer:
The current drawn from the battery is 0.5A.
---
The resistance of the bridge wire is given as 0.1Ω/cm and the length of the wire is 100cm.
The null point divides the wire in the ratio 2:3. This means that the left segment of the wire (where the unknown resistance X is connected) is 2 parts, and the right segment (where 6Ω is connected) is 3 parts.
- Length of left segment = 22+3×100cm=25×100cm=40cm
- Length of right segment = 32+3×100cm=35×100cm=60cm
Using the resistance per cm, we can calculate the resistance of each segment:
- Resistance of left segment (40 cm):
R1=0.1Ω/cm×40cm=4Ω
- Resistance of right segment (60 cm):
R2=0.1Ω/cm×60cm=6Ω
In a balanced meter bridge, the ratio of the resistances is given by:
X6=R1R2=46
X=6×46=4Ω
Now we have:
- Resistance X=4Ω
- Resistance of the wire segments: R1=4Ω and R2=6Ω
Rtotal=R1+R2=4Ω+6Ω=10Ω
Using Ohm's law, the current I drawn from the battery can be calculated as:
I=VRtotal=5V10Ω=0.5A
The current drawn from the battery is 0.5A.
Similar Questions
Knowledge Check
- Question 1 - Select One
A wire connected in the left gap of a meter bridge balance a 10Ω resistance in the right gap to a point, which divides the bridge wire in the ratio 3:2. If the length of the wire is 1m. The length of one ohm wire is
A0.057mB0.067mC0.37mD0.134m - Question 2 - Select One
In a meter bridge experiment the ratio of left gap resistance to right gap resistance is 2:3 the balance point from is
A60cmB50cmC40cmD20cm
In a meter bridge, null point is 20cm, when the known resistance R is shunted by 10Ω resistance, null point is found to be shifted by 10 cm. Find the unknown resistance X.
View SolutionIn a meter bride, null point is 20cm, when the known resistance R is shunted by 10Ω resistance, null point is found to be shifted by 10cm . Find the unknown resistance X.
View SolutionIn a metre bridge when the resistance in the left gap is 2Ω and an unknown resistance in the right gap, the balance point is obtained at 40 cm from the zero end. On shunting the unknown resistance with 2Ω find the shift of the balance point on the bridge wire.
View SolutionIn a meter bridge circuit, resistance, in the left hand gap is 2Ω and an unknown resistance X is in the right hand gap as shown in figure below. The null point is found to be 40 cm from the left end of the wire. What resistance should be connected to X so that the new null point is 50 cm from the left end of the wire ?
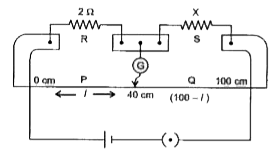 View Solution
View SolutionIn a meter bridge, the null point is found at a distance of 40 cm from A. If now a resistance of 12 Ω is connected in parallel with S, the null point occurs at 60 cm from A. Determine the value of R.
 View Solution
View SolutionIn the gives circuit, a meter bridge is shows in a balanced state. The bridge wire has a resistance of 1Ωcm−1. Find the value of the unknown resistance X and the current draws from the battery of negligible internal resistance.
 View Solution
View Solution

