In above question if resistance of meter bridge wire is 1 Ω /cm then the value of current / is
0.11 A
0.33 A
0.66 A
3.3 A
The correct Answer is:C
To solve the problem step by step, we will follow the outlined approach in the video transcript.
1. Identify the Resistance of the Meter Bridge Wire:
Given that the resistance of the meter bridge wire is 1 ohm/cm, we can calculate the resistance for different segments of the wire based on their lengths.
2. Calculate the Resistance for Each Segment:
- For the first segment (let's say R1), which is 40 cm long:
R1=40cm×1Ω/cm=40Ω
- For the second segment (let's say R2), which is 60 cm long:
R2=60cm×1Ω/cm=60Ω
3. Set Up the Balance Condition of the Meter Bridge:
The meter bridge is balanced, which gives us the following relationship:
ABBD=ACCD
Where:
- AB=X (the unknown resistance)
- BD=6Ω (the known resistance)
- AC=40Ω
- CD=60Ω
Plugging in the values:
X6=4060
4. Solve for X:
Cross-multiplying gives:
60X=240⟹X=24060=4Ω
5. Determine the Total Resistance in the Circuit:
After finding X, we can now analyze the circuit. The two resistances X and Y (which is 6 ohms) are in series:
Rtotal=X+Y=4Ω+6Ω=10Ω
6. Calculate the Equivalent Resistance of the Circuit:
The other two resistances (R1 and R2) are also in series:
Rparallel=R1+R2=40Ω+60Ω=100Ω
Now, we can find the equivalent resistance Req of the two series combinations:
Req=Rtotal×RparallelRtotal+Rparallel=10×10010+100=1000110=10011Ω
7. Calculate the Current I:
Using Ohm's law, where I=VR:
I=6VReq=610011=6×11100=66100=0.66A
Final Answer:
The value of the current I is 0.66A.
---
Given that the resistance of the meter bridge wire is 1 ohm/cm, we can calculate the resistance for different segments of the wire based on their lengths.
- For the first segment (let's say R1), which is 40 cm long:
R1=40cm×1Ω/cm=40Ω
- For the second segment (let's say R2), which is 60 cm long:
R2=60cm×1Ω/cm=60Ω
The meter bridge is balanced, which gives us the following relationship:
ABBD=ACCD
Where:
- AB=X (the unknown resistance)
- BD=6Ω (the known resistance)
- AC=40Ω
- CD=60Ω
X6=4060
Cross-multiplying gives:
60X=240⟹X=24060=4Ω
After finding X, we can now analyze the circuit. The two resistances X and Y (which is 6 ohms) are in series:
Rtotal=X+Y=4Ω+6Ω=10Ω
The other two resistances (R1 and R2) are also in series:
Rparallel=R1+R2=40Ω+60Ω=100Ω
Req=Rtotal×RparallelRtotal+Rparallel=10×10010+100=1000110=10011Ω
Using Ohm's law, where I=VR:
I=6VReq=610011=6×11100=66100=0.66A
The value of the current I is 0.66A.
Topper's Solved these Questions
Similar Questions
If not current flows through the galvanometer the find the value of unknown resistance X. Assume that resistance per unit length of wire AB is 0.2 Ω/cm.
 then also calculate total current given by battery.
then also calculate total current given by battery.
View SolutionIn balanced meter bridge, the resistance of bridge wire is 0.1Ωcm . Unknown resistance X is connected in left gap and 6Ω in right gap, null point divides the wire in the ratio 2:3 . Find the current drawn the battery of 5V having negligible resistance
View SolutionIn a wheatstone bridge resistance of each of the four sides is 10Ω. If the resistance of the galvanometer is also 10Ω , then effective resistance of the bridge will be
View SolutionIn the circuit shows in Fig. 6.20, a meter bridge is in its balance state. The meter bridge wire has a resistance of 1Ωcm−1. Calculate the value of the unknow resistance X and current drawn from the battery of negligible internal resistance.
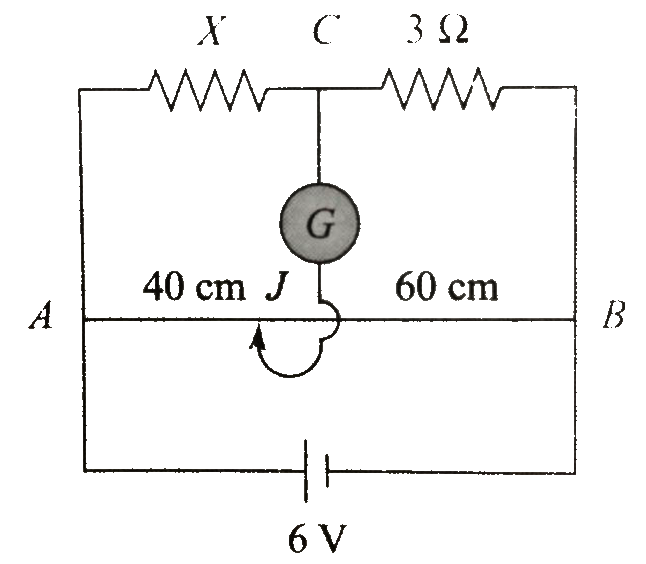
View SolutionIn the circuit shown, a meter bridge is in its balanced state. The meter bridge wire has a resistance .1ohm/cm. The value of unknown resistance X and the current drawn from the battery of negligible resistance is
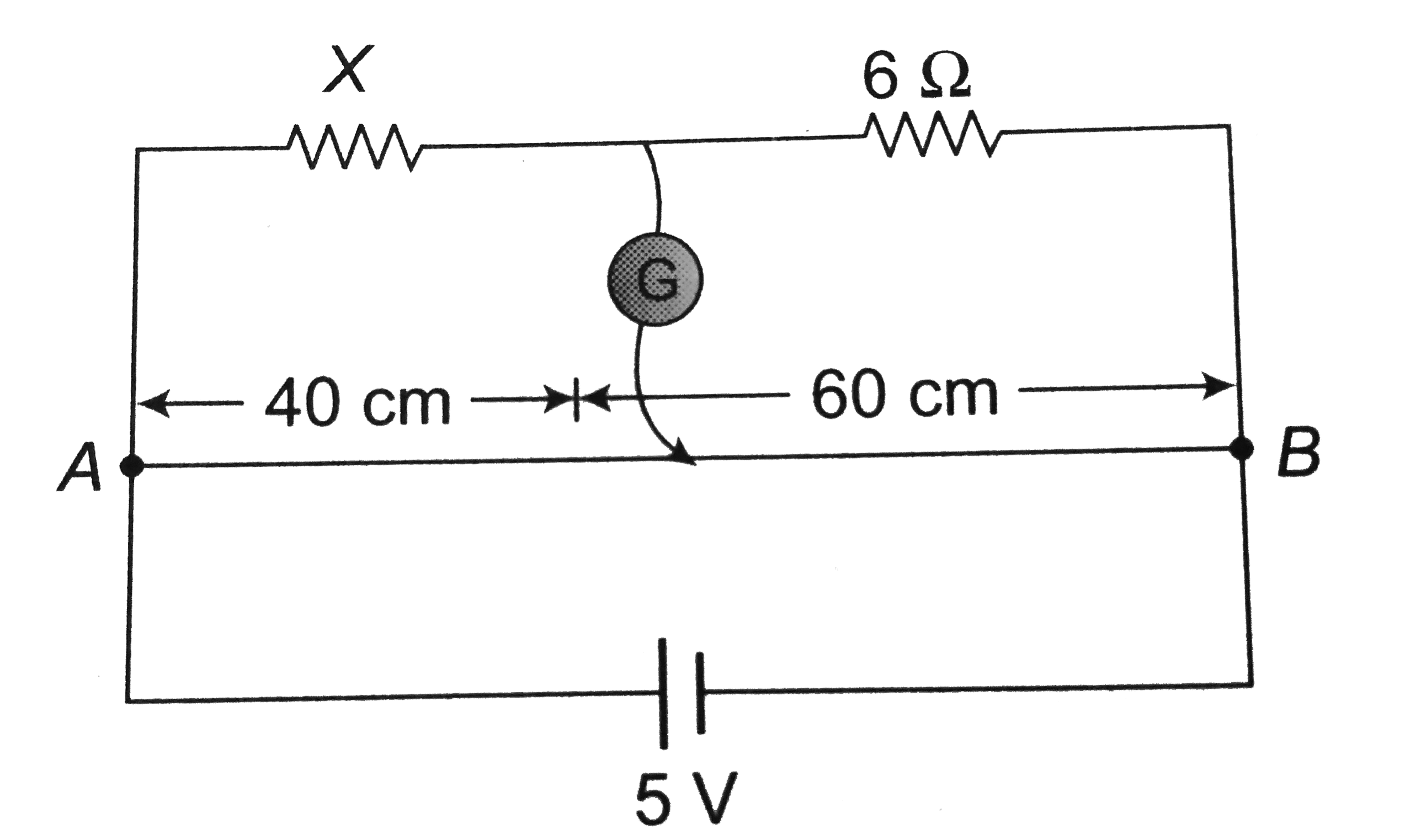
View SolutionIn the circuit shown, a meter bridge is in its balanced state. The meter bridge wire has a resistance .1ohm/cm. The value of unknown resistance X and the current drawn from the battery of negligible resistance is

View SolutionIn meter bridge experiment if, resistance S in resistance box =300Ω then the balanced length is found to be 25.0cm from end A. The diameter of unknown wire is 1mm and length of unknown wire is 31.4cm. The specific resistivity of the wire should be
View SolutionIn the gives circuit, a meter bridge is shows in a balanced state. The bridge wire has a resistance of 1Ωcm−1. Find the value of the unknown resistance X and the current draws from the battery of negligible internal resistance.

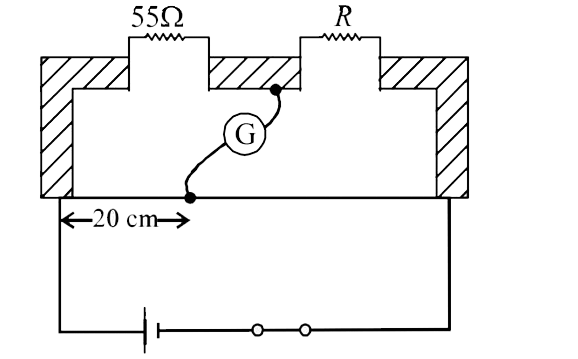
View SolutionA meter bridge setup is shown in the figure. If there is null deflection in galvanometer when length AC = 20 cm, then the value of resistance R is
View SolutionAn unknown resistance R1 is connected is series with a resistance of 10Ω. This combination is connected to one gap of a meter bridge, while other gap is connected to another resistance R2. The balance point is at 50cm Now , when the 10Ω resistance is removed, the balanced point shifts to 40cm Then the value of R1 is.
View Solution
