A ball (initially at rest) falls vertically for 2 s and hits a smooth plane inclined at 30∘ to the horizontal. The coefficient of restitution is 58. The distance along the plane between the first and second impact of the ball is
40.63 m
20.63 m
30.63 m
50.63
The correct Answer is:A
To solve the problem step by step, let's break down the given information and apply the relevant physics concepts.
Step 1: Determine the velocity of the ball just before it hits the inclined plane.
The ball falls freely for 2 seconds under the influence of gravity. The equation for velocity under constant acceleration is:
v=u+gt
Where:
- u=0 (initial velocity)
- g=10m/s2 (acceleration due to gravity)
- t=2s
Substituting the values:
v=0+(10m/s2)(2s)=20m/s
Step 2: Resolve the velocity into components along and perpendicular to the inclined plane.
The inclined plane makes an angle of 30∘ with the horizontal. We need to resolve the velocity into two components:
1. Perpendicular to the plane
2. Along the plane
Using trigonometry:
- The component of velocity perpendicular to the plane (v⊥) is given by:
v⊥=vcos(30∘)=20cos(30∘)=20(√32)=10√3m/s
- The component of velocity along the plane (v∥) is given by:
v∥=vsin(30∘)=20sin(30∘)=20(12)=10m/s
Step 3: Calculate the velocity after the first impact using the coefficient of restitution.
The coefficient of restitution e is given as 58. The relationship between the velocities before and after the impact is given by:
e=velocity of separationvelocity of approach
The velocity of approach is the perpendicular component:
velocity of approach=v⊥=10√3m/s
The velocity of separation can be calculated as:
velocity of separation=e⋅velocity of approach=58⋅10√3=50√38=25√34m/s
Step 4: Determine the new vertical component of velocity after impact.
The new vertical component of velocity after impact is:
v′⊥=v⊥−velocity of separation=10√3−25√34
Finding a common denominator:
v′⊥=40√34−25√34=15√34m/s
Step 5: Calculate the time of flight after the first impact.
The acceleration component perpendicular to the inclined plane is:
a⊥=gcos(30∘)=10⋅√32=5√3m/s2
Using the formula for time of flight t:
t=v′⊥a⊥=15√345√3=1520=34s
Step 6: Calculate the distance traveled along the inclined plane during this time.
The distance along the inclined plane can be calculated using the formula:
s=v∥t+12a∥t2
Where a∥=gsin(30∘)=10⋅12=5m/s2.
Substituting the values:
s=(10m/s)(34s)+12(5m/s2)(34s)2
Calculating each term:
1. First term: 10⋅34=7.5m
2. Second term: 12⋅5⋅916=4516=2.8125m
Adding both terms:
s=7.5+2.8125=10.3125m
Final Result
The distance along the plane between the first and second impact of the ball is approximately 10.3125m.
The ball falls freely for 2 seconds under the influence of gravity. The equation for velocity under constant acceleration is:
- u=0 (initial velocity)
- g=10m/s2 (acceleration due to gravity)
- t=2s
The inclined plane makes an angle of 30∘ with the horizontal. We need to resolve the velocity into two components:
1. Perpendicular to the plane
2. Along the plane
- The component of velocity perpendicular to the plane (v⊥) is given by:
The coefficient of restitution e is given as 58. The relationship between the velocities before and after the impact is given by:
The new vertical component of velocity after impact is:
The acceleration component perpendicular to the inclined plane is:
The distance along the inclined plane can be calculated using the formula:
2. Second term: 12⋅5⋅916=4516=2.8125m
The distance along the plane between the first and second impact of the ball is approximately 10.3125m.
Similar Questions
A ball is projected from a point in a horizontal plane with a velocity of 20 m/s at 30∘ with the horizontal. Coefficient of restitution is 0.8, then
View SolutionA partical of mass 1kg rests on rought contact with a plane inclined at 30∘ to the horizontal and is just about to slip, Find the coefficient of friction between the plane and the particle.
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionA ball is dropped on a smooth inclined plane and is observed to move horizontally after the impact. The coefficient of restitution between the plane and ball is e. The inclination of the plane is
View SolutionA ball falls from height h over an inclined plane of inclination 30∘ as shown. After the collision, the ball moves horizontally, the coefficient of restitution is
_PHY_224_Q01.png)
View SolutionA ball is dropped from a certain height on a horizontal floor. The coefficient of restitution between the ball and the floor is 12. The displacement time graph of the ball will be.
View SolutionA particle falling vertically from a height hits a plane surface inclined to horizontal at an ange θ with speed v0 and rebounds elastically (Fig. 2 (RP). 28). Find the distance aling the plane where it will hit second time.
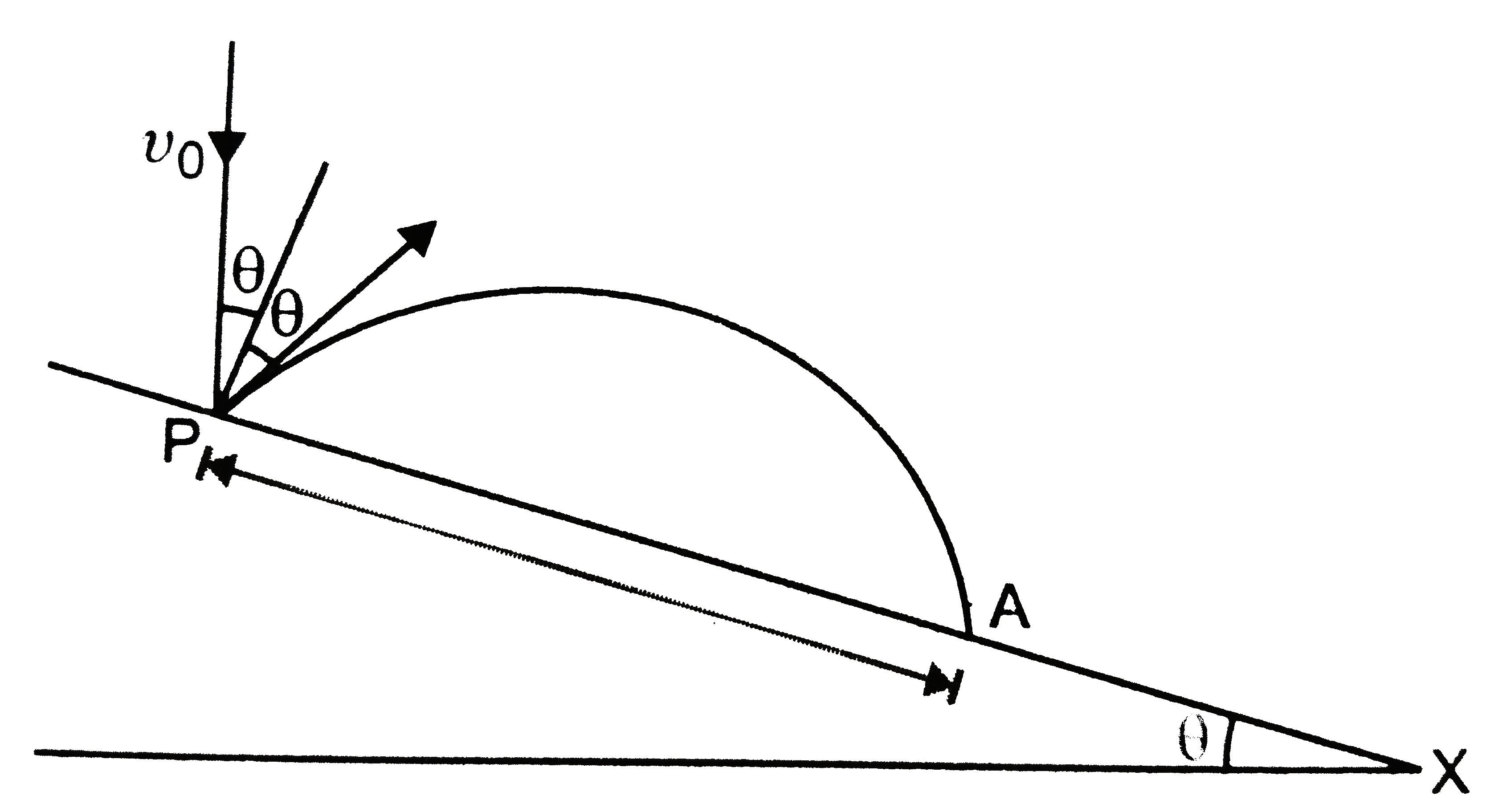 .
.
View SolutionA ball falls from height h over an inclined plane of inclination 30°C as shown. After the collision, the ball moves horizontally, the coefficient of restitution is
_PHY_E05_227_Q001.png)
View SolutionA ball is projected in a direction inclined to the vertical and bounces on a smooth horizontal plane. The range of one rebound is R. If the coefficient of restitution is e, then range of the next rebound is
View SolutionA ball after freely falling from a height of 4.9m strikes a horizontal plane. If the coefficient of restitution is 34, the ball will strike second time with the plane after
View Solution
