Two cylindrical conductors with equal cross-sections and different resistivites ρ1 and ρ2 are point end to end. Find the charge at the boundary of the conduction if a current I flows from conductor 1 to conductor 2
ε0(ρ2−ρ1)l
ε0(2ρ2+ρ1)l
2ε0(ρ1−ρ2)l
ε0(ρ1+ρ2)l
The correct Answer is:A
To solve the problem of finding the charge at the boundary of the two cylindrical conductors when a current I flows from conductor 1 to conductor 2, we can follow these steps:
Step 1: Understand the Current Density
Since both conductors have equal cross-sectional areas A and carry the same current I, the current density J can be defined as:
J=IA
Step 2: Relate Electric Field and Current Density
Using Ohm's Law, the electric field E in each conductor can be expressed in terms of the resistivity ρ and the current density J:
E1=ρ1J(for conductor 1)
E2=ρ2J(for conductor 2)
Step 3: Apply Gauss's Law
According to Gauss's Law, the integral of the electric field E over a closed surface is equal to the charge enclosed divided by the permittivity of free space ϵ:
∮E⋅dS=Qenclosedϵ
For the boundary between the two conductors, we can write:
E2−E1=σϵ
where σ is the surface charge density at the boundary.
Step 4: Substitute Electric Fields
Substituting the expressions for E1 and E2:
ρ2J−ρ1J=σϵ
This simplifies to:
(ρ2−ρ1)J=σϵ
Step 5: Solve for Surface Charge Density
Rearranging gives us the surface charge density σ:
σ=ϵ(ρ2−ρ1)J
Step 6: Calculate the Total Charge at the Boundary
The total charge Q at the boundary can be found by multiplying the surface charge density σ by the area A:
Q=σA=ϵ(ρ2−ρ1)JA
Substituting J=IA:
Q=ϵ(ρ2−ρ1)(IA)A
This simplifies to:
Q=ϵ(ρ2−ρ1)I
Final Answer
Thus, the charge at the boundary of the conductors is:
Q=ϵ(ρ2−ρ1)I
Since both conductors have equal cross-sectional areas A and carry the same current I, the current density J can be defined as:
J=IA
Using Ohm's Law, the electric field E in each conductor can be expressed in terms of the resistivity ρ and the current density J:
E1=ρ1J(for conductor 1)
E2=ρ2J(for conductor 2)
According to Gauss's Law, the integral of the electric field E over a closed surface is equal to the charge enclosed divided by the permittivity of free space ϵ:
∮E⋅dS=Qenclosedϵ
For the boundary between the two conductors, we can write:
E2−E1=σϵ
where σ is the surface charge density at the boundary.
Substituting the expressions for E1 and E2:
ρ2J−ρ1J=σϵ
This simplifies to:
(ρ2−ρ1)J=σϵ
Rearranging gives us the surface charge density σ:
σ=ϵ(ρ2−ρ1)J
The total charge Q at the boundary can be found by multiplying the surface charge density σ by the area A:
Q=σA=ϵ(ρ2−ρ1)JA
Substituting J=IA:
Q=ϵ(ρ2−ρ1)(IA)A
This simplifies to:
Q=ϵ(ρ2−ρ1)I
Thus, the charge at the boundary of the conductors is:
Q=ϵ(ρ2−ρ1)I
Similar Questions
Equal masses of two substance of densities ρ1andρ2 are mixed together. What is the density of the mixture?
View SolutionConsider a conductor of variable cross section in which current is flowing from cross section 1 to 2. Then
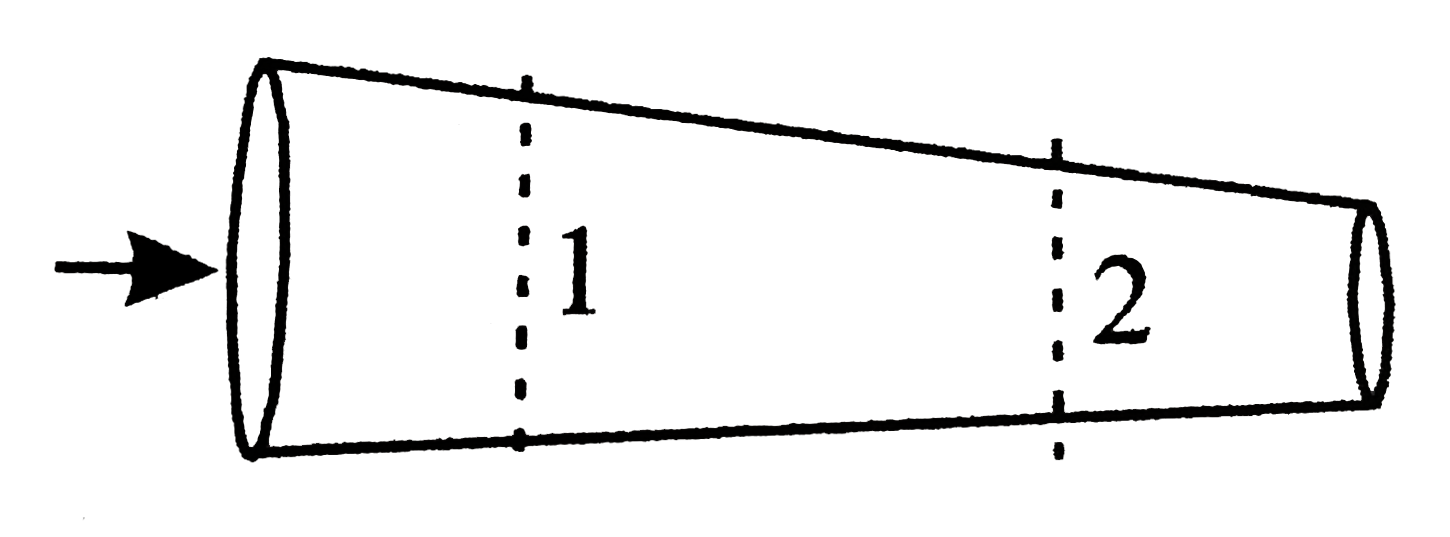
View SolutionIf the potential difference across the ends of a conductor is doubled, the current flowing through it gets
View Solution
A cylindrical conductor of length l and inner radius R1 and outer radius R2 has specific resistance ρ. A cell of emf ε is connected across the two lateral faces of the conductor. Find the current drown from the cell.
View SolutionA cylindrical conductor of length l and uniform area of cross-section A has resistance R. Another conductor of length 2l and resistance R of the same material has area of cross-section :
View SolutionA cylinder conductor AB of non uniform area of cross-section carries a current of 5A. The radius of the conductor at one end A is 0.5 cm.The current density at the other end of the conductor is half of the value at A. The radius of the conductor at the end B is nearly
View SolutionWhen two isolated conductors A and B are connected by a conducting wire positive charge will flow from .
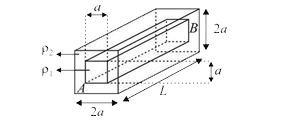
View SolutionA composite rod made up of two conductors of resistivity ρ1 and ρ2 is shown in the figure. If face A and B are connected to a battery, find the resistance of the rod.
View SolutionA cylindrical conductor has uniform cross-section. Resistivity of its material increase linearly from left end to right end. If a constant current is flowing through it and at a section distance x from left end, magnitude of electric field intensity is E , which of the following graphs is correct
View SolutionA cylindrical conductor has uniform cross-section. Resistivity of its material increase linearly from left end to right end. If a constant current is flowing through it and at a section distance x from left end, magnitude of electric field intensity is E , which of the following graphs is correct
View Solution
