A flat mirror revolves at a constant angular velocity making n=0.4 revolutions per second. With what velocity (in m s−1) will a light spot move along a spherical screen with a radius of 15 m, if the mirror is at the centre of curvature of the screen ?
37.7
60.3
68.7
75.4
The correct Answer is:D
To solve the problem, we need to determine the velocity of a light spot moving along a spherical screen when a flat mirror revolves at a constant angular velocity. Here are the steps to find the solution:
1. Identify Given Values:
- Angular velocity in revolutions per second, n=0.4revolutions/second
- Radius of the spherical screen, r=15m
2. Convert Angular Velocity to Radians:
- Since 1revolution=2πradians, we convert the angular velocity from revolutions per second to radians per second:
ω=n×2π=0.4×2π=0.8πradians/second
3. Determine Angular Velocity of Reflected Light:
- The angular velocity of the reflected rays is twice the angular velocity of the mirror:
ωreflected=2×ω=2×0.8π=1.6πradians/second
4. Calculate the Velocity of the Light Spot:
- The velocity v of the light spot on the spherical screen can be calculated using the formula:
v=r×ωreflected
- Substituting the values:
v=15m×1.6πradians/second
- Calculating this gives:
v=15×1.6×3.14≈75.4m/s
5. Final Answer:
- The velocity of the light spot moving along the spherical screen is approximately 75.4m/s.
Summary:
The light spot moves along the spherical screen with a velocity of approximately 75.4m/s.
- Angular velocity in revolutions per second, n=0.4revolutions/second
- Radius of the spherical screen, r=15m
- Since 1revolution=2πradians, we convert the angular velocity from revolutions per second to radians per second:
ω=n×2π=0.4×2π=0.8πradians/second
- The angular velocity of the reflected rays is twice the angular velocity of the mirror:
ωreflected=2×ω=2×0.8π=1.6πradians/second
- The velocity v of the light spot on the spherical screen can be calculated using the formula:
v=r×ωreflected
- Substituting the values:
v=15m×1.6πradians/second
- Calculating this gives:
v=15×1.6×3.14≈75.4m/s
- The velocity of the light spot moving along the spherical screen is approximately 75.4m/s.
The light spot moves along the spherical screen with a velocity of approximately 75.4m/s.
Similar Questions
A small source of sound vibrating frequency 500 Hz is rotated in a circle of radius 100π cm at a constant angular speed of 5.0 revolutions per second. The speed of sound in air is 330ms.
Q. If the observer moves towards the source with a constant speed of 20ms, along the radial line to the centre, the fractional change in the apparent frequency over the frequency that the source will have if considered at reat at the centre will be
View SolutionA particle is moving along a circle of radius 20cm, with a linear velocity of 2m//s. Calculate the angular velocity of the particle.
View SolutionA particle is moving along a circle of radius 20cm, with a linear velocity of 2m//s. Calculate the angular velocity of the particle.
View SolutionA partical revolves in clockwise direction (as seen from point A) in a circle C of radius 1 cm and completes one revolution in 2 sec. The axis of the circle and the principal axis of the mirror M coincides, call it AB. The radius of curvature of the mirror of 20cm. Then, the direction of revolution (as seen from A) of the image of the partical and its speed is
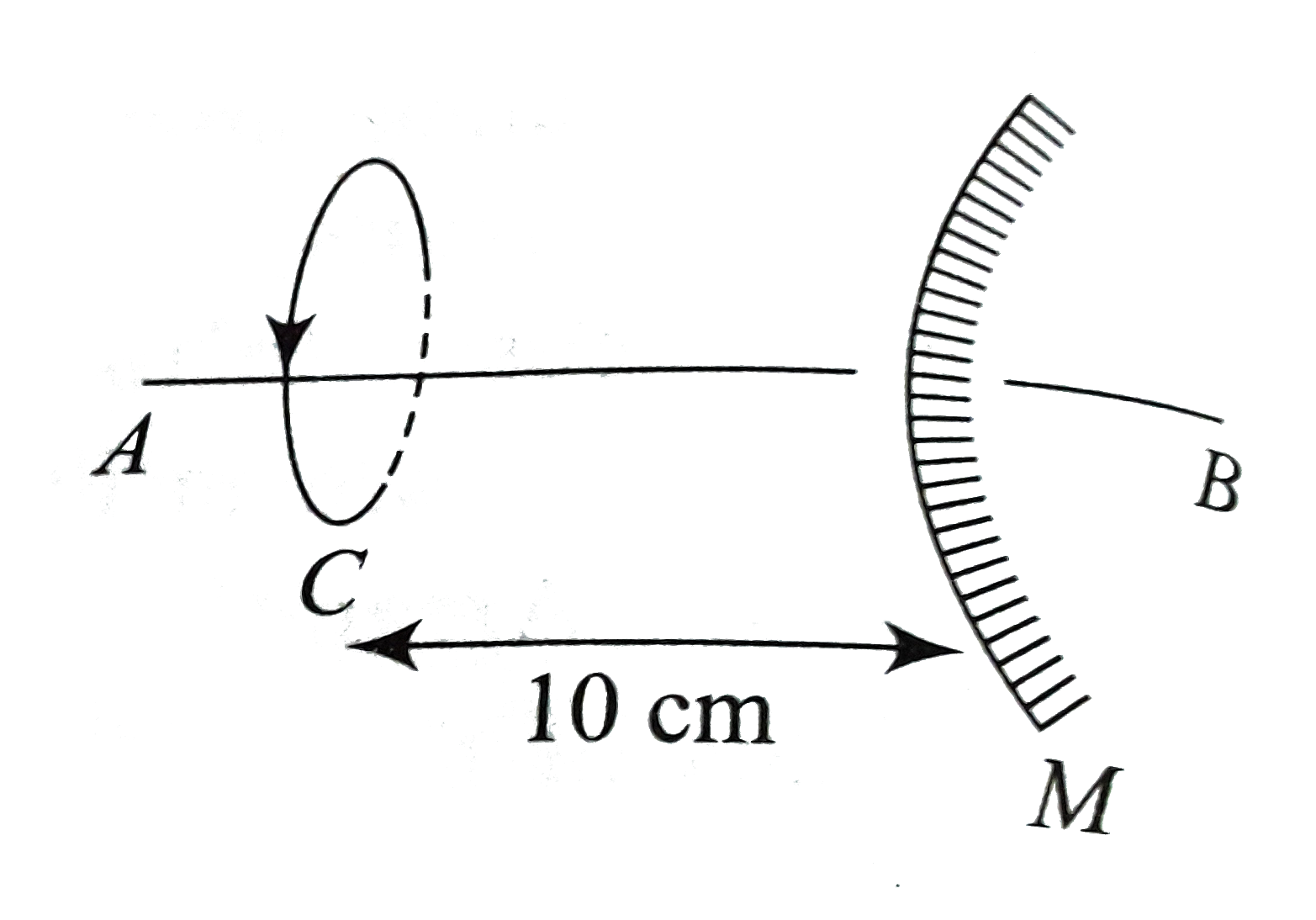
View SolutionA 0.5 kg ball moves in a circle of radius 0.4 m at a velocity of 4 m/s. The centripetal force on the ball is
View SolutionA particle starts with a velocity of 2m/s and moves in a straight line with a retardation of 0.1m/s2. The time that it takes to describe 15m is
View SolutionA point object O and a mirror M move with velocities of 3cms−1 and 4cms−1 , respectively as shown in the figure. OO' is the normal to the mirror. What is the velocity of the image?

View SolutionA disc of mass 1 kg and radius 0.1 m is rotating with angular velocity 20 rad s−1. What is angular velocity, if a mass of 0.25 kg is put on periphery of the disc?
View SolutionA disc of mass 2 kg and radius 0.2 m is rotating with angular velocity 30rad s−1. What is angular velocity, if a mass of 0.25 kg is put on periphery of the disc ?
View SolutionA spot light S rotates in a horizontal plane with a constant angular velocity of 0.1rad/s. The spot of light P move along the wall at a disatnce 3m. What is the velocity of the spot P when θ=45∘ ?
View Solution
