A very long straight conducting wire, lying along the z-axis, carries a current of 2A. The integral ∮→B.d→l is computed along the straight line PQ, where P has the coordinates (2cm,0,0) and Q has the coordinates (2cm,2cm,0). The integral has the magnitude (in SI units)
zero
8π×10−7
2π×10−7
π×10−7
The correct Answer is:D
To solve the problem, we need to compute the integral ∮→B⋅d→l along the straight line from point P to point Q, where the wire carrying a current of 2A lies along the z-axis.
Step 1: Understanding the Magnetic Field Due to a Long Straight Wire
The magnetic field →B due to a long straight wire carrying a current I is given by the formula:
B=μ0I2πr
where:
- μ0 is the permeability of free space, approximately 4π×10−7T m/A,
- I is the current (2A in this case),
- r is the perpendicular distance from the wire to the point where the magnetic field is being calculated.
Step 2: Determine the Path of Integration
The points P and Q are given as:
- P(2cm,0,0)
- Q(2cm,2cm,0)
The path from P to Q is along the y-axis at a constant x-coordinate of 2 cm. The distance from the wire (located on the z-axis) to the path is:
r=2cm=0.02m
Step 3: Calculate the Magnetic Field at Points P and Q
Using the formula for the magnetic field:
B=μ0⋅22π⋅0.02
Substituting μ0=4π×10−7:
B=(4π×10−7)⋅22π⋅0.02=4×10−7⋅20.04=8×10−70.04=2×10−5T
Step 4: Set Up the Integral
The integral ∮→B⋅d→l can be evaluated along the straight line from P to Q. Since the magnetic field is perpendicular to the path of integration (which is along the y-axis), the angle between →B and d→l is 90 degrees. Thus:
→B⋅d→l=B⋅dl⋅cos(90∘)=0
Step 5: Conclusion
Since the magnetic field is perpendicular to the path of integration, the integral evaluates to zero:
∮→B⋅d→l=0
Final Answer
The magnitude of the integral ∮→B⋅d→l is:
0
The magnetic field →B due to a long straight wire carrying a current I is given by the formula:
B=μ0I2πr
where:
- μ0 is the permeability of free space, approximately 4π×10−7T m/A,
- I is the current (2A in this case),
- r is the perpendicular distance from the wire to the point where the magnetic field is being calculated.
The points P and Q are given as:
- P(2cm,0,0)
- Q(2cm,2cm,0)
r=2cm=0.02m
Using the formula for the magnetic field:
B=μ0⋅22π⋅0.02
Substituting μ0=4π×10−7:
B=(4π×10−7)⋅22π⋅0.02=4×10−7⋅20.04=8×10−70.04=2×10−5T
The integral ∮→B⋅d→l can be evaluated along the straight line from P to Q. Since the magnetic field is perpendicular to the path of integration (which is along the y-axis), the angle between →B and d→l is 90 degrees. Thus:
→B⋅d→l=B⋅dl⋅cos(90∘)=0
Since the magnetic field is perpendicular to the path of integration, the integral evaluates to zero:
∮→B⋅d→l=0
The magnitude of the integral ∮→B⋅d→l is:
0
Similar Questions
A very long straight conducting wire, lying along the z-axis, carries a current of 2A. The integral ∮→B.d→l is computed along the straight line PQ, where P has the coordinates (2cm,2cm,0) and Q has the coordinates (2cm,2cm,0). The integral has the magnitude (in SI units)
View SolutionA long straight wire along the z- axis carries a current I in the negative z−direction . The magnetic vector field →B at a point having coordinates (x,y) in the Z=0 plane is
View SolutionA long straight wire along the z- axis carries a current I in the negative z−direction . The magnetic vector field →B at a point having coordinates (x,y) in the Z=0 plane is
View SolutionA very long straight wire carries a current I. At the instant when a charge +Q at point P has velocity →V, as shown, the force on the charge is
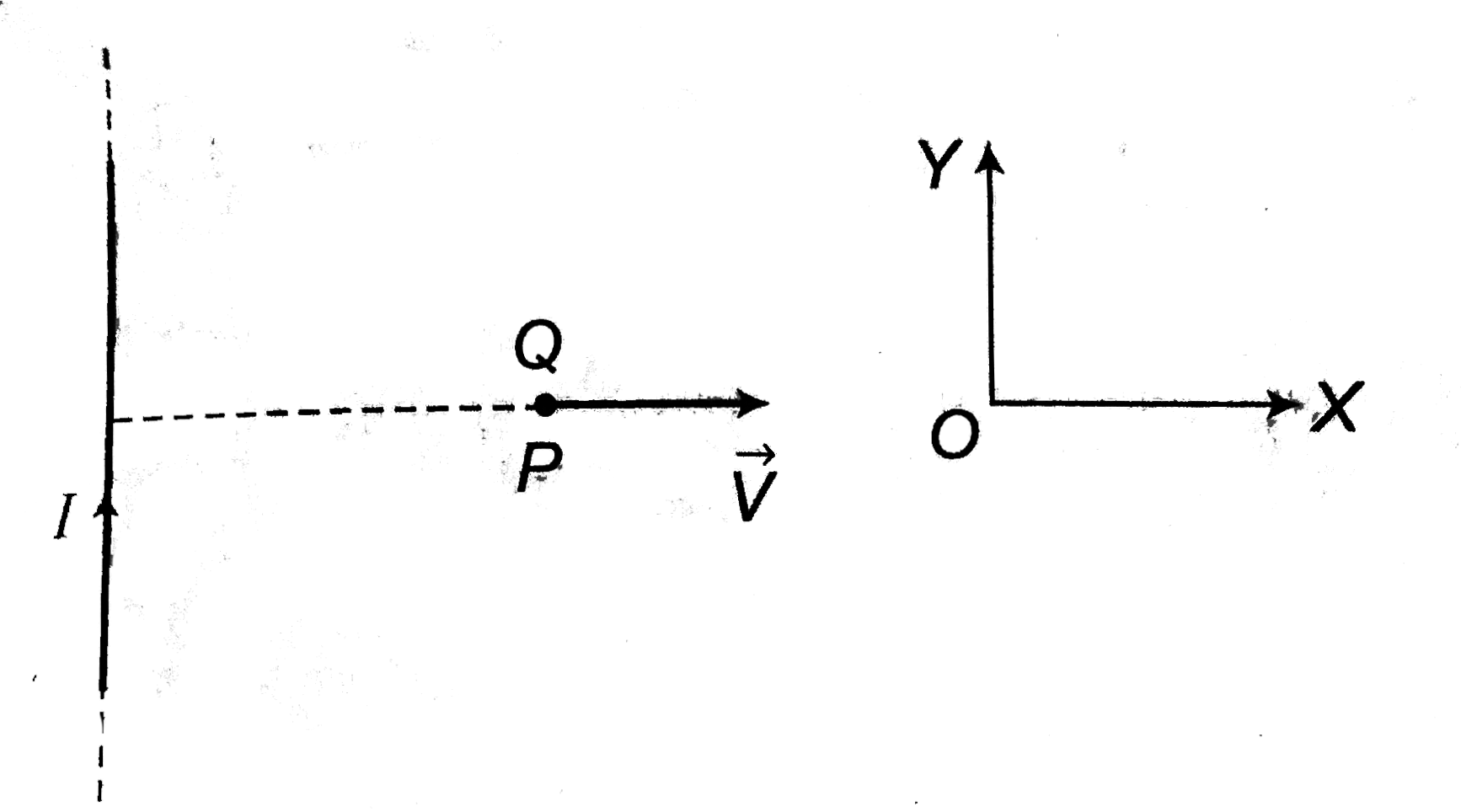
View SolutionA very long straight wire carries a current I. At the instant when a charge +Q at point P has velocity→V, as shown, the force on the charge is-
View SolutionA point Q at a distance 3 from the point P(1,1,1) lying on the line joining the points
A(0,−1,3) and P has the coordinates
View SolutionFind a unit vector in the direction of −−→PQ, where P and Q have coordinates (5, 0, 8) and (3, 3, 2) respectively.
View SolutionIn the ΔABC, the coordinates of B are (0,0),AB=2,∠ABC=π3 and the middle point of BC has the coordinates (2,0). The centroid of the triangle is
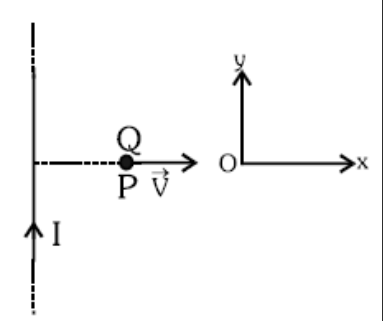
View Solutiona very long straight wire carries a current I. at the instant when are charge -Q at point P has velocity v as shown in figure the force on the charge is

View SolutionPoint A lies on the curve y=ex2 and has the coordinate (x,e−x2) where x>0. Point B has the coordinates (x,0). If 'O' is the origin, then the maximum area of the ΔAOB is
View Solution
