When a Daniel cell is connected in the secondary circuit of a potentiometer, the balancing length is found to be 540 cm. If the balancing length becomes 500 cm. When the cell is short-circuited with 1Ω, the internal resistance of the cell is
The correct Answer is:0.08
To find the internal resistance of the Daniel cell when it is short-circuited, we can follow these steps:
Step 1: Understand the initial conditions
When the Daniel cell is connected to the potentiometer, the balancing length is 540 cm. This means that the potential difference (E) across the cell can be expressed as:
E=V0×L1
where V0 is the potential drop per unit length of the potentiometer wire and L1=540cm.
Step 2: Understand the conditions when the cell is short-circuited
When the cell is short-circuited with a 1 ohm resistor, the balancing length changes to 500 cm. The potential difference across the battery can now be expressed as:
E=V0×L2
where L2=500cm.
Step 3: Set up the equations
From the two conditions, we can set up the following equations:
1. E=V0×540
2. E=I×(R+1) where I is the current through the circuit and R is the internal resistance of the cell.
Step 4: Calculate the current when short-circuited
The current I can be expressed as:
I=ER+1
Step 5: Relate the two equations
From the second condition, we can express the potential difference across the external circuit (1 ohm resistor) as:
E=I×1=I
Substituting I from the previous equation gives:
E=ER+1
Step 6: Substitute the values of balancing lengths
Now, we can relate the two expressions for E:
V0×540V0×500=1R+1
This simplifies to:
540500=1R+1
Step 7: Solve for R
Cross-multiplying gives:
540(R+1)=500
540R+540=500
540R=500−540
540R=−40
R=−40540=−227
Step 8: Correct the approach
Since we are looking for internal resistance, we should have:
R+1=540500
R+1=2725
R=2725−1=27−2525=225
Step 9: Final answer
Thus, the internal resistance R of the cell is:
R=0.08Ω
When the Daniel cell is connected to the potentiometer, the balancing length is 540 cm. This means that the potential difference (E) across the cell can be expressed as:
E=V0×L1
where V0 is the potential drop per unit length of the potentiometer wire and L1=540cm.
When the cell is short-circuited with a 1 ohm resistor, the balancing length changes to 500 cm. The potential difference across the battery can now be expressed as:
E=V0×L2
where L2=500cm.
From the two conditions, we can set up the following equations:
1. E=V0×540
2. E=I×(R+1) where I is the current through the circuit and R is the internal resistance of the cell.
The current I can be expressed as:
I=ER+1
From the second condition, we can express the potential difference across the external circuit (1 ohm resistor) as:
E=I×1=I
E=ER+1
Now, we can relate the two expressions for E:
V0×540V0×500=1R+1
540500=1R+1
Cross-multiplying gives:
540(R+1)=500
540R+540=500
540R=500−540
540R=−40
R=−40540=−227
Since we are looking for internal resistance, we should have:
R+1=540500
R+1=2725
R=2725−1=27−2525=225
Thus, the internal resistance R of the cell is:
R=0.08Ω
Similar Questions
When 6 identical cells of no internal resistance are connected in series in the secondarycircuit of a potentio meter, the balancing lengths is .l., balancing length becomes 1/3 when some cells are connected wrongly, the number of cells connected wrongly are
View SolutionThe adjoining figure shows the connection of potentiometer experiment to determine internal resistance of a leclanche cell. When the cell is an open circuit the balancing length of the potentiometer wire is 3 .4m and on closing the key K2 the balancing length becomes 17.m. If the resistance R through which current is dream is 10Ω then the internal resistance of the cell is:
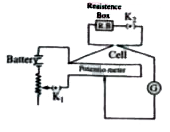
View Solution
Knowledge Check
In a potentiometer the balancing with a cell is at length of 220cm. On shunting the cell with a resistance of 3Ω balance length becomes 130cm. What is the internal resistance of this cell.
A4.5ΩB7.8ΩC6.3ΩD2.08Ω
In a potentiometer experiment the balancing with a cell is at length 240 cm. On shunting the cell with a resistance of 2Ω, the balancing length becomes 120 cm.The internal resistance of the cell is
View SolutionIn an experiment to determine the internal resistance of a cell with potentiometer, the balancing length is 165 cm. When a resistance of 5 ohm is joined in parallel with the cell the balancing length is 150 cm. The internal resistance of cell is
View SolutionIn an experiment to measure the internal resistance of a cell by a potentiometer, it is found that the balance point is at a length of 2m when the cell is shunted by a 5Ω resistance and is at a length of 3m when the cell is shunted by a 10Ω resistance, the internal resistance of the cell is then
View SolutionFor the given circuit,
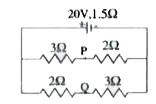
If internal resistance of cell is 1.5Ω, then
View SolutionTwo cells of E.M.F. E1 and E2(E2>E1) are connected in series in the secondary circuit of a potentiometer experiment for determination of E.M.F. The balancing length is found to be 825 cm. Now when the terminals to cell E1 are reversed, then the balancing length is found to be 225 cm. The ratio of E1 and E2 is
View SolutionIn an experiment to measure the internal resistance of a cell by potentiometer, it is found that the balance point is at a length of 2 m when the cell is shunted by a 4Ω resistance and at 3 m when cell is shunted by a 8Ω resistance. The internal resistance of cell is -
View SolutionIn a potentiometer experiment the balancing length with a cell is 560 cm. When an external resistance of 10Ω is connected in parallel to the cell, the balancing length changes by 60 cm. Find the internal resistance of the cell.
View Solution