A particle is moving in a force field given by potential energy U=−λ(x+y+z)from point (1,1,1) to (2, 3, 4). The work done in the process is
3λ
1.5λ
6λ
12λ
The correct Answer is:C
To solve the problem, we need to calculate the work done by a particle moving in a force field defined by the potential energy function U=−λ(x+y+z) as it moves from point (1,1,1) to point (2,3,4).
Step 1: Identify the initial and final points
The initial point is (x1,y1,z1)=(1,1,1) and the final point is (x2,y2,z2)=(2,3,4).
Step 2: Calculate the potential energy at the initial point
Using the potential energy formula:
U1=−λ(x1+y1+z1)=−λ(1+1+1)=−λ⋅3=−3λ
Step 3: Calculate the potential energy at the final point
Using the potential energy formula:
U2=−λ(x2+y2+z2)=−λ(2+3+4)=−λ⋅9=−9λ
Step 4: Calculate the change in potential energy
The change in potential energy ΔU as the particle moves from the initial point to the final point is given by:
ΔU=U2−U1=(−9λ)−(−3λ)=−9λ+3λ=−6λ
Step 5: Relate the change in potential energy to work done
According to the work-energy theorem, the work done W by conservative forces is equal to the negative of the change in potential energy:
W=−ΔU=−(−6λ)=6λ
Conclusion
The work done in the process of moving from point (1,1,1) to point (2,3,4) is:
6λ
The initial point is (x1,y1,z1)=(1,1,1) and the final point is (x2,y2,z2)=(2,3,4).
Using the potential energy formula:
U1=−λ(x1+y1+z1)=−λ(1+1+1)=−λ⋅3=−3λ
Using the potential energy formula:
U2=−λ(x2+y2+z2)=−λ(2+3+4)=−λ⋅9=−9λ
The change in potential energy ΔU as the particle moves from the initial point to the final point is given by:
ΔU=U2−U1=(−9λ)−(−3λ)=−9λ+3λ=−6λ
According to the work-energy theorem, the work done W by conservative forces is equal to the negative of the change in potential energy:
W=−ΔU=−(−6λ)=6λ
The work done in the process of moving from point (1,1,1) to point (2,3,4) is:
6λ
Similar Questions
A particale moves under the effect of a force F=Cx from x=0 to x=x1. The work down in the process is
View SolutionA particle is acted upon by a force →F=yˆi+xˆj newton. When the particle is moved from (1 m, 1 m) to (9m, 3 m) via straight path, work done by →F is y. What is the value of xy?
View Solution
Knowledge Check
A particle in a certain conservative force field has a potential energy given by V=20xyz. The force exerted on it is
A(20yz)ˆi+(20xz)ˆj+(20xyz2)ˆkB−(20yz)ˆi−(20xz)ˆj+(20xyz2)ˆkC−(20yz)ˆi−(20xz)ˆj−(20xyz2)ˆkD(20yz)ˆi+(20xz)ˆj−(20xyz2)ˆk
A particle moves in one dimension in a conservation force field. The potential energy is depicted in the graph below.
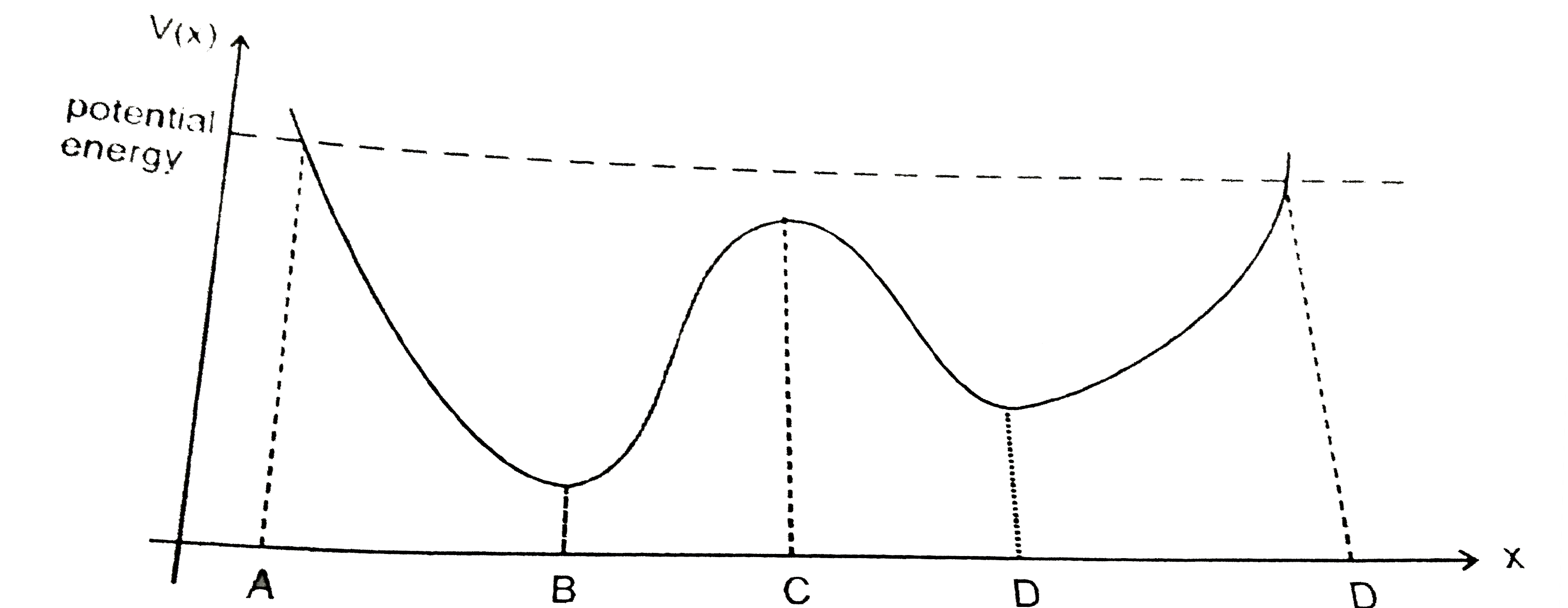
If the particle starts to move from rest from the point A, then
View SolutionA particle moves in one dimension in a conservation force field. The potential energy is depicted in the graph below.

If the particle starts to move from rest from the point A, then
View SolutionA force bar F = (3hat i-4 hat j +b hat k)N is acting on the particle which is moving from point A ( 0-1, 1) m to the point B(2, 2 3) m If net work done by the force on the particle is zero then value of b is
View SolutionA charge is moved in an electric field of a fixed charge distribution from point A to another point B slowly. The work done by external agent in doing so is 100J . What is the change in potential energy of the charge as it moves from A to B ? What is the work done by the electric field of the charge distribution as the charge moves from A to B ?
View SolutionA charge is moved in an electric field of a fixed charge distribution from point A to another point B slowly. The work done by external agent in doing so is 100J. What is the change in potential energy of the charge as it moves from A to B ? What is the work done by the electric field of the charge distribution as the charge moves from A to B ?
View SolutionA particle is moving in a conservative force field from point A to point B.UA and UB are the potential energies of the particle at point A and B and WC is the work done by conservative forces in the process of taking the particle from A and B, which of the following is true?
View SolutionA particle of mass m=3 kg is moving on a straight line in a conservative force field in which the potential energy associated with the particle is given by U(y)=2y2−30y+450. At t=0, particle is at y=8m and moving towards positive y- axis with 1m/s
View Solution
