In the primary circuit of a potentiometer, a cell of E.M.F 1 V and a rheostat of 15Ω are connected in series. If the resistance of the potentiometer wire is 10Ω the minimum voltage at the ends of the wire (in V) will be
0.1
0.4
0.06
1.0
The correct Answer is:B
To solve the problem step by step, we will use the principles of electrical circuits, specifically applying Kirchhoff's voltage law.
Step 1: Understand the Circuit Configuration
We have a circuit consisting of:
- A cell with an EMF (E) of 1 V.
- A rheostat (variable resistor) with a resistance (R_H) of 15 Ω.
- A potentiometer wire with a resistance (R_W) of 10 Ω.
Step 2: Apply Kirchhoff's Voltage Law
According to Kirchhoff's voltage law, the sum of the potential differences (voltage) in a closed loop is equal to the EMF of the sources in that loop.
The equation can be set up as follows:
E−I⋅RW−I⋅RH=0
Where:
- E=1V (EMF of the cell)
- RW=10Ω (resistance of the potentiometer wire)
- RH=15Ω (resistance of the rheostat)
- I is the current flowing through the circuit.
Step 3: Rearrange the Equation
Rearranging the equation gives:
E=I⋅(RW+RH)
Step 4: Substitute Known Values
Substituting the known values into the equation:
1=I⋅(10+15)
1=I⋅25
Step 5: Solve for Current (I)
Now, solve for the current I:
I=125A
Step 6: Calculate the Minimum Voltage Across the Potentiometer Wire
The voltage across the potentiometer wire (V_AB) can be calculated using Ohm's Law:
VAB=I⋅RW
Substituting the values:
VAB=(125)⋅10
VAB=1025=0.4V
Conclusion
The minimum voltage at the ends of the potentiometer wire is 0.4 V.
---
We have a circuit consisting of:
- A cell with an EMF (E) of 1 V.
- A rheostat (variable resistor) with a resistance (R_H) of 15 Ω.
- A potentiometer wire with a resistance (R_W) of 10 Ω.
According to Kirchhoff's voltage law, the sum of the potential differences (voltage) in a closed loop is equal to the EMF of the sources in that loop.
E−I⋅RW−I⋅RH=0
- E=1V (EMF of the cell)
- RW=10Ω (resistance of the potentiometer wire)
- RH=15Ω (resistance of the rheostat)
- I is the current flowing through the circuit.
Rearranging the equation gives:
E=I⋅(RW+RH)
Substituting the known values into the equation:
1=I⋅(10+15)
1=I⋅25
Now, solve for the current I:
I=125A
The voltage across the potentiometer wire (V_AB) can be calculated using Ohm's Law:
VAB=I⋅RW
Substituting the values:
VAB=(125)⋅10
VAB=1025=0.4V
The minimum voltage at the ends of the potentiometer wire is 0.4 V.
Similar Questions
A 2 V battery, a 990Ω resistor and a potentiometer of 2 m length, all are connected in series of the resistance of potentiometer wire is 10Ω, then the potential gradient of the potentiometer wire is
View SolutionA 2 V battery, a 990Ω resistor and a potentiometer of 2 m length, all are connected in series of the resistance of potentiometer wire is 10Ω, then the potential gradient of the potentiometer wire is
View SolutionA potentiometer wire of length 1 m has a resistance of 10Ω. It is connected to a 6V battery in series with a resistance of 5Ω. Determine the emf of the primary cell which gives a balance point at 40cm.
View SolutionIn fig. battery E is balanced on 55cm length of potentiometer wire but when a resistance of 10Ω is connected in parallel with the battery then it balances on 50cm length of the potentiometer wire then internal resistance r of the battery is:-
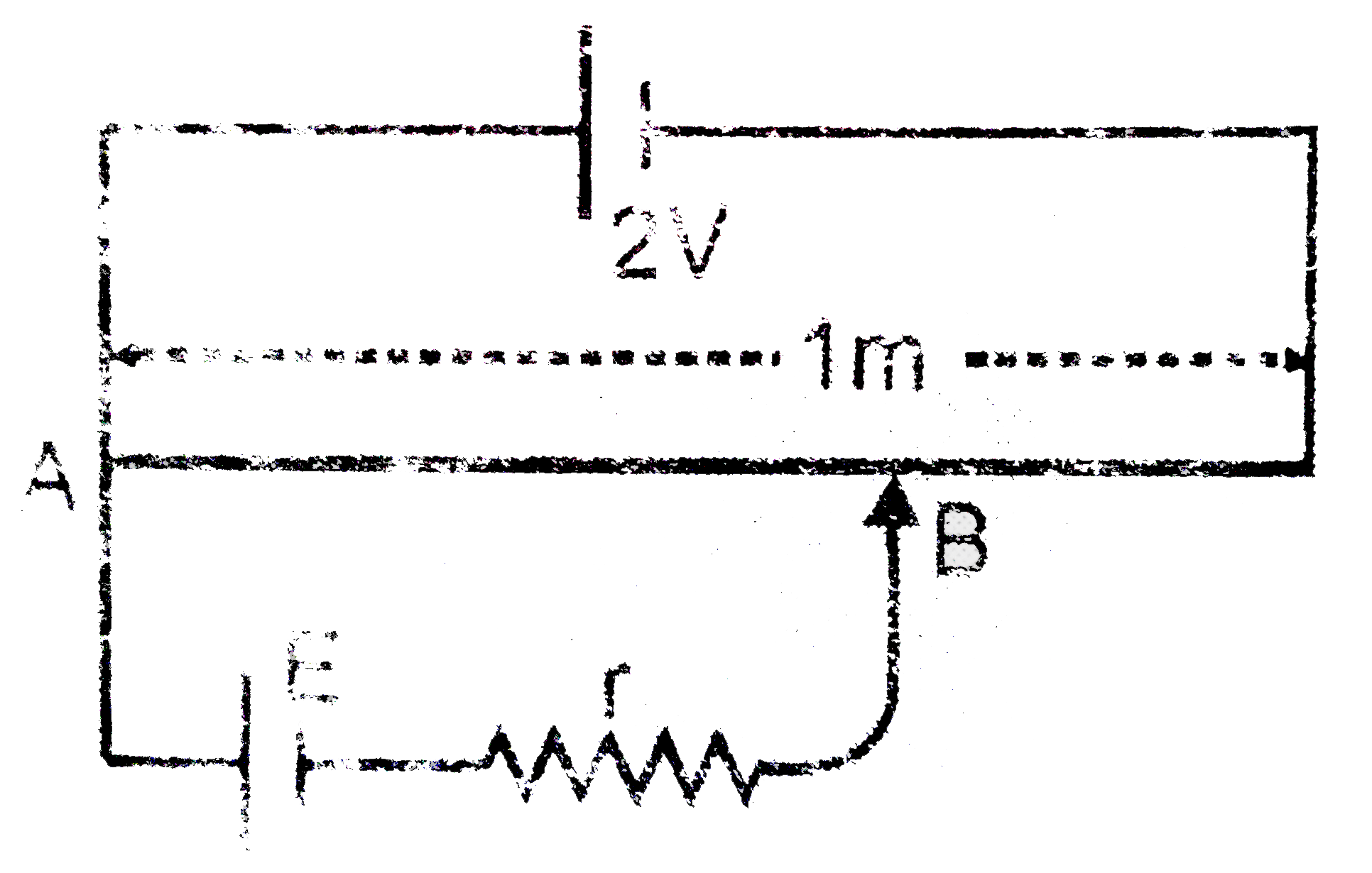
View SolutionA cell of e.m.f. 1.8 V and internal resistance 2 Ω is connected in series with an ammeter of resistance 0.7 Ω and a resistor of 4.5 Ω as shown in Fig.
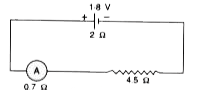
What would be the reading of the ammeter ?
View SolutionA potentiometer wire of length 1.0 m has a resistance of 15 ohm. It is connected to a 5 V source in series with a resistance of 5Ω. Determine the emf of the primary cell which has a balance point at 60 cm.
View SolutionA potentiometer consists of a wire of length 4 m and resistance 10Ω. It is connected to a cell of emf 2V.The potential gradient of the wire is
View SolutionA potentiometer wire 10 long has a resistance of 40Ω. It is connected in series with a resistances box and a 2 v storage cell. If the potential gradient along the wire is 0.01Vm the resistance unplugged in the box is
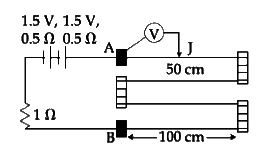
View SolutionIn the circuit shown, a four-wire potentiometer is made of a 400cm long wire, which extents between A and B . The resistance per unit length of the potentiometer wire is rL=0.01Ω/cm. If an ideal voltmeter is connected as shown with jockey J at 50 cm from end A, the expected reading of the voltmeter will be :
View SolutionA cell whose e.m.f. is 2V and internal resistance is 0.1Ω is connected with a resistance of 3.9Ω the voltage across the cell terminal will be
View Solution
