The centre of mass of three particles of masses 1 kg, 2 kg and 3 kg is at (2,2, 2). The position of the fourth mass of 4 kg to be placed in the system as that the new centre of mass is at (0, 0, 0) is
(−3,−3,−3)
(−3,3,−3)
(2,3,−3)
(2,−2,3)
The correct Answer is:A
To find the position of the fourth mass (4 kg) such that the new center of mass of the system is at (0, 0, 0), we can follow these steps:
Step 1: Understand the Given Data
We have three masses:
- m1=1kg
- m2=2kg
- m3=3kg
The center of mass of these three particles is given as (2,2,2).
Step 2: Calculate the Total Mass
The total mass of the three particles is:
M=m1+m2+m3=1+2+3=6kg
Step 3: Use the Center of Mass Formula
The formula for the center of mass (xcm,ycm,zcm) of a system of particles is given by:
xcm=m1x1+m2x2+m3x3m1+m2+m3
Similarly for ycm and zcm.
Given that the center of mass is at (2,2,2), we can write:
m1x1+m2x2+m3x3=12(for x-coordinate)
m1y1+m2y2+m3y3=12(for y-coordinate)
m1z1+m2z2+m3z3=12(for z-coordinate)
Step 4: Introduce the Fourth Mass
Let the position of the fourth mass m4=4kg be (x4,y4,z4).
The new center of mass after adding the fourth mass should be at (0,0,0). Thus, we can write:
x′cm=m1x1+m2x2+m3x3+m4x4m1+m2+m3+m4=0
y′cm=m1y1+m2y2+m3y3+m4y4m1+m2+m3+m4=0
z′cm=m1z1+m2z2+m3z3+m4z4m1+m2+m3+m4=0
Step 5: Set Up the Equations
Substituting the known values into the equations:
12+4x410=0⇒12+4x4=0⇒4x4=−12⇒x4=−3
12+4y410=0⇒12+4y4=0⇒4y4=−12⇒y4=−3
12+4z410=0⇒12+4z4=0⇒4z4=−12⇒z4=−3
Step 6: Conclusion
Thus, the position of the fourth mass should be:
(x4,y4,z4)=(−3,−3,−3)
We have three masses:
- m1=1kg
- m2=2kg
- m3=3kg
The total mass of the three particles is:
M=m1+m2+m3=1+2+3=6kg
The formula for the center of mass (xcm,ycm,zcm) of a system of particles is given by:
xcm=m1x1+m2x2+m3x3m1+m2+m3
Similarly for ycm and zcm.
m1x1+m2x2+m3x3=12(for x-coordinate)
m1y1+m2y2+m3y3=12(for y-coordinate)
m1z1+m2z2+m3z3=12(for z-coordinate)
Let the position of the fourth mass m4=4kg be (x4,y4,z4).
x′cm=m1x1+m2x2+m3x3+m4x4m1+m2+m3+m4=0
y′cm=m1y1+m2y2+m3y3+m4y4m1+m2+m3+m4=0
z′cm=m1z1+m2z2+m3z3+m4z4m1+m2+m3+m4=0
Substituting the known values into the equations:
12+4x410=0⇒12+4x4=0⇒4x4=−12⇒x4=−3
12+4y410=0⇒12+4y4=0⇒4y4=−12⇒y4=−3
12+4z410=0⇒12+4z4=0⇒4z4=−12⇒z4=−3
Thus, the position of the fourth mass should be:
(x4,y4,z4)=(−3,−3,−3)
Similar Questions
The coordinates of the centre of mass of a system of three particles of mass 1g,2g and 3g are (2,2,2). Where should a fourth particle of mass 4 g be positioned so that the centre of mass of the four particle system is at the origin of the three-dimensional coordinate system ?
View SolutionCentre of mass of two particle with masses 2 kg and 1 kg locsted at (1, 0, 1) and (2, 2, 0) has the co - ordinates of
View Solution
Knowledge Check
Centre of mass of three particles of masses 1kg,2kgand3kg lies at the point (1,2,3) and centre of mass of another system of particles 3kgand2kg lies at the point (−1,3,−2). Where should we put a particle of mass 5kg so that the centre of mass of entire system lies at the centre of mass of first system ?
A(0, 0, 0)B(1, 3, 2)C(-1, 2, 3)D(3, 1, 8)Three particles of masses 1kg,32kg,and2kg are located the vertices of an equilateral triangle of side a. The x,y coordinates of the centre of mass are.
Aa. 5a9,2a3√3Bb. 2a3√3,5a9Cc. 5a9,2a√3Dd. 2a√3,5a9
Two particles of masses 1kg and 2kg are located at x=0 and x=3m. Find the position of their centre of mass.
View SolutionTwo particles of masses 1kg and 2kg are located at x=0 and x=3m. Find the position of their centre of mass.
View SolutionThree point particles of masses 1.0 kg, 1.5 kg and 2.5 kg are placed at three corners of a right angle triangle as shown in figure. The centre of mass of the system is at a point :
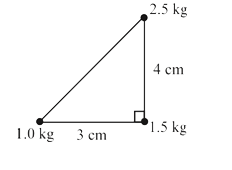
View SolutionThree point particles of masses 1.0 kg, 1.5 kg and 2.5 kg are placed at three corners of a right angle triangle as shown in figure. The centre of mass of the system is at a point :

View SolutionLocate the centre of mass of a system of three particles 1.0 kg, 2.0 kg and 3.0 kg placed at the corners of an equilateral traingular of side 1m.
View SolutionTwo bodies of masses 10 kg and 20 kg are located in x-y plane at (0, 1) and (1, 0). The position of their centre of mass is
View Solution
