Three masses of 2 kg, 4 kg and 4 kg are placed at the three points (1, 0, 0), (1, 1, 0) and (0, 1, 0) respectively. The position vector of its centre of massis
35ˆi+45ˆj
(3ˆi+ˆj)
25gati+45ˆj
15ˆi+35ˆj
To find the position vector of the center of mass of the three given masses, we can follow these steps:
Step 1: Identify the masses and their coordinates
We have three masses:
- Mass m1=2kg at position r1=(1,0,0)
- Mass m2=4kg at position r2=(1,1,0)
- Mass m3=4kg at position r3=(0,1,0)
Step 2: Write the formula for the center of mass
The position vector of the center of mass Rcm is given by the formula:
Rcm=m1r1+m2r2+m3r3m1+m2+m3
Step 3: Substitute the values into the formula
Substituting the values of the masses and their respective position vectors:
Rcm=2⋅(1,0,0)+4⋅(1,1,0)+4⋅(0,1,0)2+4+4
Step 4: Calculate the numerator
Calculating each term in the numerator:
1. For m1:
2⋅(1,0,0)=(2,0,0)
2. For m2:
4⋅(1,1,0)=(4,4,0)
3. For m3:
4⋅(0,1,0)=(0,4,0)
Now, adding these vectors together:
(2,0,0)+(4,4,0)+(0,4,0)=(2+4+0,0+4+4,0+0+0)=(6,8,0)
Step 5: Calculate the denominator
The total mass is:
m1+m2+m3=2+4+4=10
Step 6: Divide the sum of the vectors by the total mass
Now, we can find the center of mass vector:
Rcm=(6,8,0)10=(610,810,0)=(35,45,0)
Final Answer
The position vector of the center of mass is:
Rcm=(35,45,0)
---
We have three masses:
- Mass m1=2kg at position r1=(1,0,0)
- Mass m2=4kg at position r2=(1,1,0)
- Mass m3=4kg at position r3=(0,1,0)
The position vector of the center of mass Rcm is given by the formula:
Substituting the values of the masses and their respective position vectors:
Calculating each term in the numerator:
2⋅(1,0,0)=(2,0,0)
2. For m2:
4⋅(1,1,0)=(4,4,0)
3. For m3:
4⋅(0,1,0)=(0,4,0)
The total mass is:
Now, we can find the center of mass vector:
The position vector of the center of mass is:
Topper's Solved these Questions
- System of particles & rotational MotionBOOK - SL ARORACHAPTER - System of particles & rotational MotionEXERCISE - EXERCISE
353 Videos
- ROTATIONAL MOTIONBOOK - SL ARORACHAPTER - ROTATIONAL MOTIONEXERCISE - Problem for self practice
90 Videos
- Thermal Properties of MatterBOOK - SL ARORACHAPTER - Thermal Properties of MatterEXERCISE - Exercise
449 Videos
Similar Questions
Point masses 1,2,3and4kg are lying at the point (0,0,0),(2,0,0),(0,3,0) and (–2,–2,0) respectively. The moment of inertia of this system about x-axis will be
View SolutionThree point masses of 1kg,2kgand3kg lie at (1,2),(0,−1)and(2,−3) respectively. Calculate the co-ordinates of the centre of mass of the system.
View Solution
Knowledge Check
The centres of three spherical masses of 1 kg, 2 kg and 3 kg have co-orinates (4,0) m,(0,3)m and (-2,5)m respectively. What is the position vector of its centre of mass is terms of its x and y co-ordinates?
A→Rcm=2ˆi+3ˆjB→RcM=13ˆi+52ˆjCveRcm=≡−13ˆi+3.5ˆjD→rcm=23ˆi−53ˆjTwo bodies of mass 2 kg and 5 kg have position (1 m, 2 m, 1 m) and (3 m, 2 m, -1 m) respectively. The position vector of centre of mass is
A(177ˆi+2ˆj−37ˆk)mB(17ˆi+14ˆj−3ˆk)mC(2ˆi+177ˆj−37ˆk)mD(14ˆi+17ˆj−3ˆk)mThree bodies of masses 3kg, 2kg and 1 kg kept at points (3ˆi+2ˆj),(5ˆj+ˆk) and (2ˆi+ˆk) respectively. Then the position vector of their centre of mass is given by
A→Rcm=11ˆi6+38ˆj+2ˆkB→Rcm=11ˆi6+83ˆj+ˆk2C→Rcm=7ˆi6+58ˆj+2ˆkD→RCM=11ˆi6+85ˆj+3ˆk
Four particles of masses 1kg,2kg,3kg and 4kg are placed the four vertices A,B,C and D, respectively, of a square of side 1m. Find the position of centre of mass of the particles.
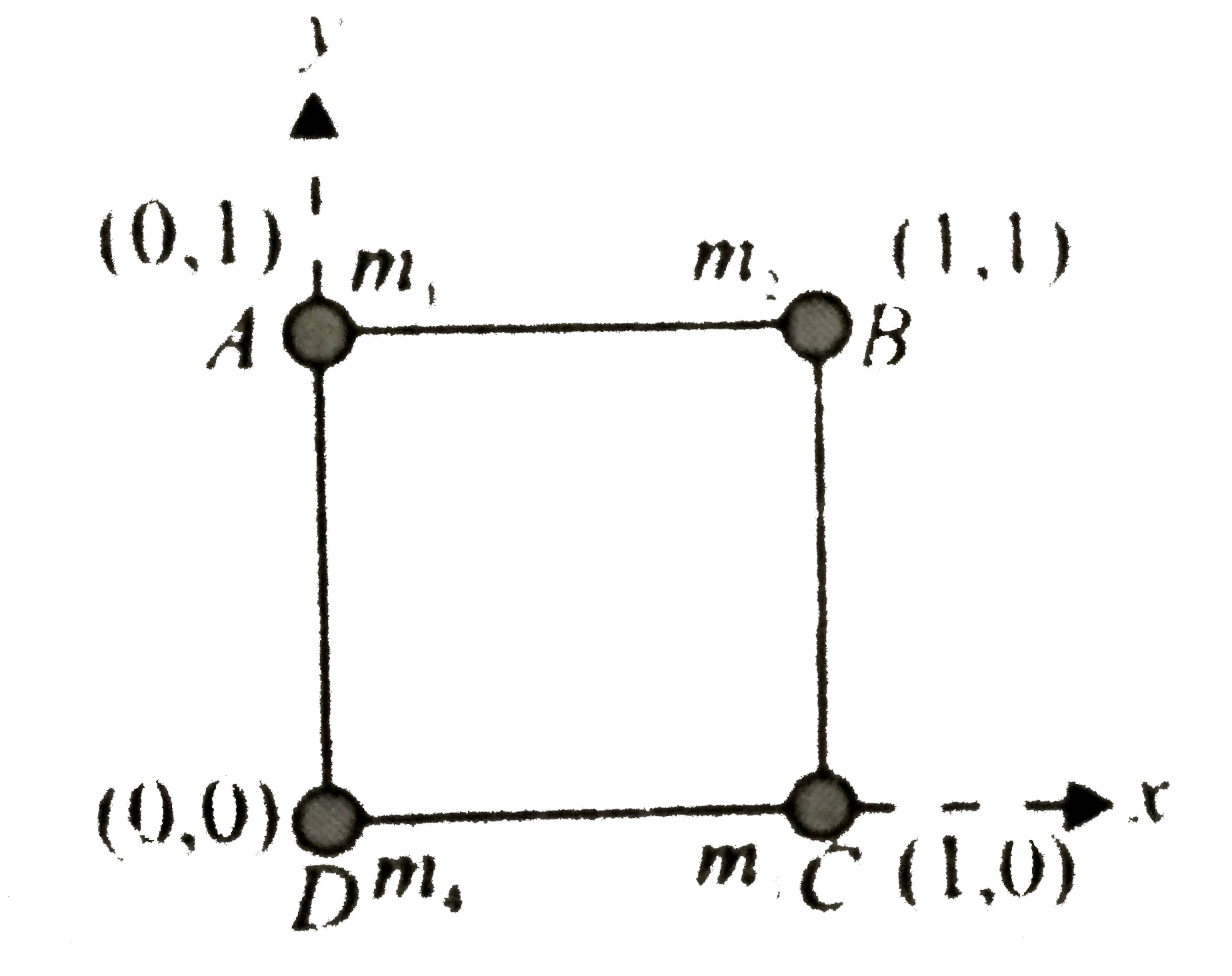
View SolutionThree point masses of 1kg, 2kg and 3kg lie at (0,0), (1,2), (3,−1) respectively. Calculate the coordinates of the centre of mass of the system.
View SolutionPoint masses of 2 kg, 3 kg, 5 kg and 7 kg are placed at the corners of a square ABCD respectively whose each side is 1 m long. The position of the centre of mass of the system is
View SolutionFour particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A, B, C and D of a square of side 1m. Find the position of centre of mass of the particles.
View SolutionThree point charges 1μC,1μC and −2μC are placed at points having coordinates (0,1,0)cm, (1,0,0) cm and (0,0,0)cm respectively. The magnitude of electric dipole moment of the system is
View Solution
