How does the electric field (E) between the plates of a charged cylindrical capacitor vary with the distance r from the axis of the cylinder ?
E∝1r2
E∝1r
E∝r2
E∝r
The correct Answer is:B
To determine how the electric field (E) between the plates of a charged cylindrical capacitor varies with the distance (r) from the axis of the cylinder, we can follow these steps:
Step 1: Understand the Configuration
We have a cylindrical capacitor consisting of two coaxial cylinders. The inner cylinder has a linear charge density of +λ, and the outer cylinder has a linear charge density of -λ. The outer cylinder is grounded, meaning its potential is zero.
Step 2: Identify the Regions
1. Inside the inner cylinder (r < B): The electric field (E) is zero because there is no charge enclosed.
2. Between the inner and outer cylinders (B < r < A): This is the region where we need to determine the electric field.
3. Outside the outer cylinder (r > A): The electric field (E) is again zero.
Step 3: Apply Gauss's Law
To find the electric field in the region between the cylinders (B < r < A), we apply Gauss's Law, which states:
∮E⋅dA=Qencϵ0
Step 4: Choose a Gaussian Surface
We consider a cylindrical Gaussian surface of radius r (where B < r < A) and height L. The area vector dA is directed outward, and the electric field E is also directed outward.
Step 5: Calculate the Left Side of Gauss's Law
The left side of Gauss's Law becomes:
∮E⋅dA=E⋅(2πrL)
Step 6: Calculate the Charge Enclosed
The charge enclosed by the Gaussian surface is given by the linear charge density of the inner cylinder:
Qenc=λL
Step 7: Set Up the Equation
Substituting the left and right sides into Gauss's Law gives:
E⋅(2πrL)=λLϵ0
Step 8: Solve for Electric Field (E)
Now, we can solve for the electric field E:
E=λ2πrϵ0
Step 9: Analyze the Result
From the equation E=λ2πrϵ0, we see that the electric field E is inversely proportional to the distance r from the axis of the cylinder. This means that as you move away from the inner cylinder, the electric field decreases.
Conclusion
The electric field between the plates of a charged cylindrical capacitor varies inversely with the distance r from the axis of the cylinder.
---
We have a cylindrical capacitor consisting of two coaxial cylinders. The inner cylinder has a linear charge density of +λ, and the outer cylinder has a linear charge density of -λ. The outer cylinder is grounded, meaning its potential is zero.
1. Inside the inner cylinder (r < B): The electric field (E) is zero because there is no charge enclosed.
2. Between the inner and outer cylinders (B < r < A): This is the region where we need to determine the electric field.
3. Outside the outer cylinder (r > A): The electric field (E) is again zero.
To find the electric field in the region between the cylinders (B < r < A), we apply Gauss's Law, which states:
We consider a cylindrical Gaussian surface of radius r (where B < r < A) and height L. The area vector dA is directed outward, and the electric field E is also directed outward.
The left side of Gauss's Law becomes:
The charge enclosed by the Gaussian surface is given by the linear charge density of the inner cylinder:
Substituting the left and right sides into Gauss's Law gives:
Now, we can solve for the electric field E:
From the equation E=λ2πrϵ0, we see that the electric field E is inversely proportional to the distance r from the axis of the cylinder. This means that as you move away from the inner cylinder, the electric field decreases.
The electric field between the plates of a charged cylindrical capacitor varies inversely with the distance r from the axis of the cylinder.
Similar Questions
A parallel plate capacitor has an electric field of 105V/m between the plates. If the charge on the capacitor plate is 1μC, then force on each capacitor plate is-
View SolutionThe weight of an object on the surface of the Earth is 40 N. Its weight at a height equal to the radius of the Earth is
View Solution
Knowledge Check
The magnitude of electric field →E in the annular region of a charged cylindrical capacitor.
Ais the same throughoutBis higher near the outer cylinder than near the inner cylinderCvaries as 1r2 where r is the distance from the axisDvaries as 1r3 where r is the distance from the axis.As the distance between the plates of a parallel plate capacitor decreased
AIf both assertion and reason are ture and reason is the correct explanation of assertion.BIf both assertin and reason are ture but reason is not the correct explanation of assertion .CIf assertion is true but reason is false.DIf both assertion and reason are false.Electric field intensity (E) due to an electric dipole varies with distance (r ) from the point of the center of dipole as :
A1rand1r2B1r2and1rC1r3and1r3D1r3and1r2
Answer the following:
(a) When a parallel plate capacitor is connected across a dc battery, explain briefly how the capacitor gets charged.
(b) A parallel plate capacitor of capacitance 'C' is charged to 'V' volt by a battery. After some time the battery is disconnected and the distance between the plates is doubled. Now a slab of dielectric constant 1<k<2 is introduced to fill the space between the plates. How will the following be affected ?
(i) The electric field between the plates of the capacitor.
(ii) The energy stored in the capacitor. Justify your answer in each case.
(c) The electric potential as a function of distance 'x' is shown in the figure. Draw a graph of the electric field E as a function of x.
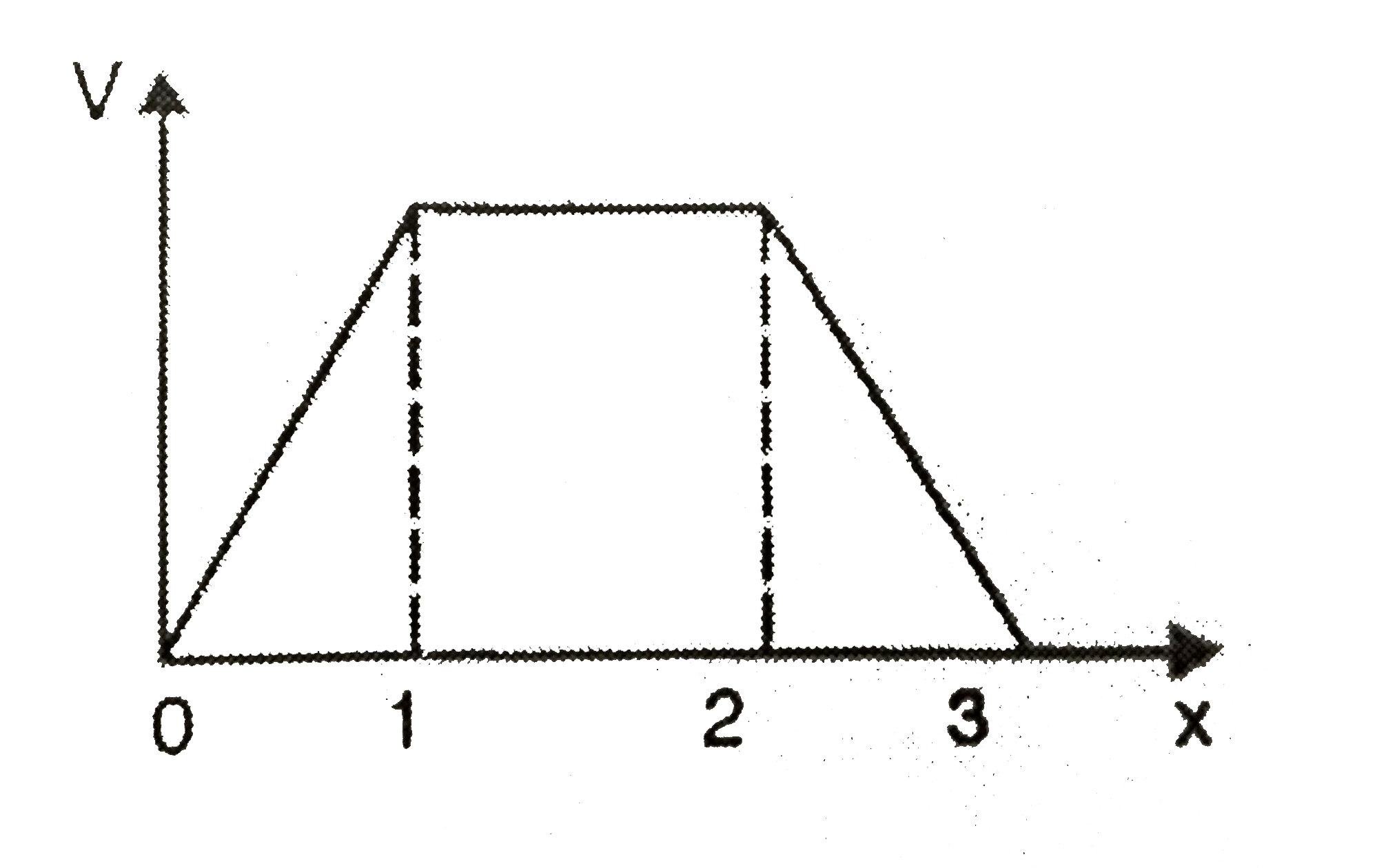
View SolutionA cylinder of radius R and length l is placed in a uniform electric field E parallel to the axis of the cylinder. The total flux over the curved surface of the cylinder is
View SolutionTwo parallel-plate capacitors with different distances between the plates are connected in parallel to a voltage source. A point positive charge is moved from a point A, that is exactly in the middle between the plates of a capacitor C1 to a point B(or a capacitor C2 that lies at a distance from the negative plate of C2 equal to half the distance between the plates of C1) During this process of moving the charge.
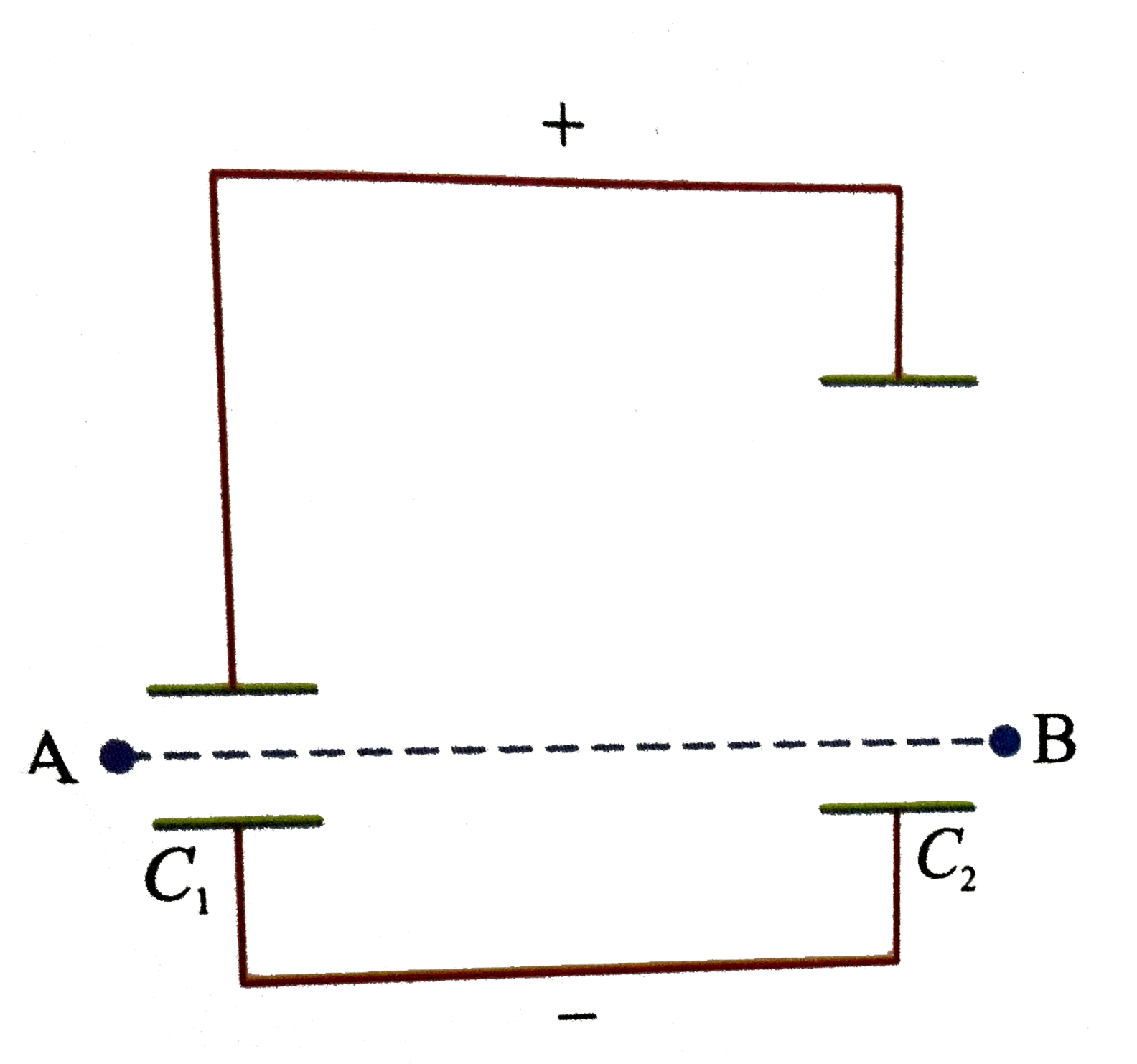 .
.
View SolutionA point charge q is placed at the origin . How does the electric field due to the charge very with distance r from the origin ?
View SolutionA long cylindrical volume contains a uniformly distributed charge of density ρ. Find the electric field at a point P inside the cylindrical volume at a distance x from its axis (figure 30-E5) ,
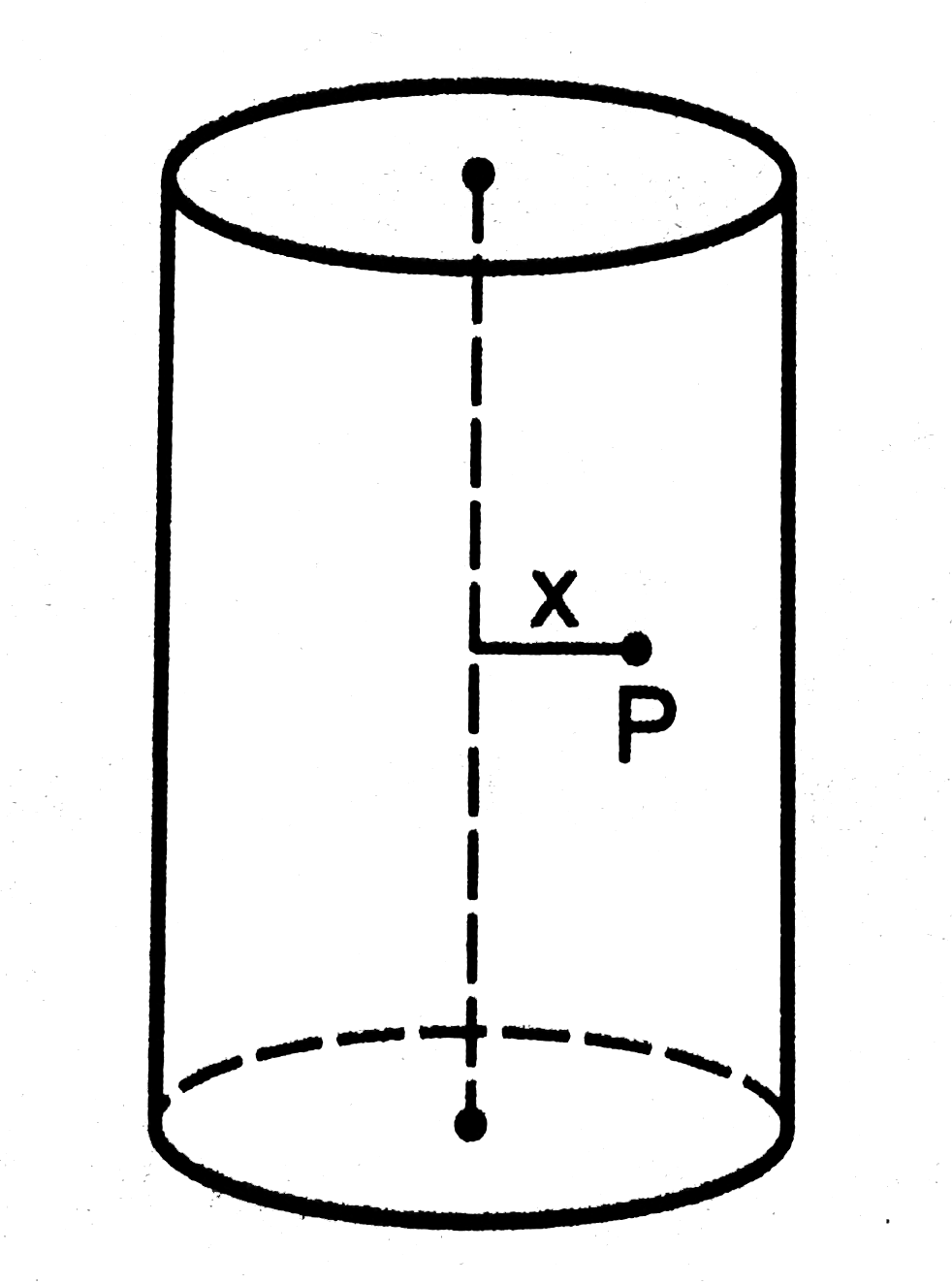
View Solution
