In a circular motion of a particle , the tangential acceleration of the particle is given by at=9ms−2 . The radius of the circle is 4m . The particle was initially at rest. Time after which total acceleration of the particle makes an angle of 45∘ with the radial acceleration is
(a)13s
(b)23s
(c)53s
(d)43s
The correct Answer is:B
To solve the problem, we need to find the time after which the total acceleration of the particle makes an angle of 45∘ with the radial acceleration. Here are the steps to arrive at the solution:
Step 1: Understand the relationship between tangential and radial acceleration
We know that the total acceleration A of a particle in circular motion can be resolved into two components: tangential acceleration at and radial (centripetal) acceleration ar. The angle θ between the total acceleration and the radial acceleration is given by:
tan(θ)=atar
Step 2: Set up the equation for the angle
Given that the angle θ=45∘, we have:
tan(45∘)=1⟹at=ar
Step 3: Calculate the radial acceleration
The radial acceleration ar is given by the formula:
ar=v2r
where v is the velocity of the particle and r is the radius of the circular path. We know from the problem that r=4m.
Step 4: Relate tangential acceleration to velocity
We are given that the tangential acceleration at=9m/s2. Setting at equal to ar gives us:
9=v24
Step 5: Solve for velocity v
From the equation above, we can solve for v:
v2=9×4=36⟹v=√36=6m/s
Step 6: Relate tangential acceleration to time
The tangential acceleration is also defined as the rate of change of velocity:
at=dvdt
Substituting the known value of at:
9=dvdt
Step 7: Integrate to find time t
To find the time t taken to reach the velocity of 6m/s:
∫60dv=∫t09dt
This gives us:
6−0=9t−0⟹6=9t
Step 8: Solve for t
Now, solving for t:
t=69=23s
Conclusion
The time after which the total acceleration of the particle makes an angle of 45∘ with the radial acceleration is:
23s
We know that the total acceleration A of a particle in circular motion can be resolved into two components: tangential acceleration at and radial (centripetal) acceleration ar. The angle θ between the total acceleration and the radial acceleration is given by:
Given that the angle θ=45∘, we have:
The radial acceleration ar is given by the formula:
We are given that the tangential acceleration at=9m/s2. Setting at equal to ar gives us:
From the equation above, we can solve for v:
The tangential acceleration is also defined as the rate of change of velocity:
To find the time t taken to reach the velocity of 6m/s:
Now, solving for t:
The time after which the total acceleration of the particle makes an angle of 45∘ with the radial acceleration is:
Similar Questions
In a circular motion of a particle the tangential acceleration of the particle is given by a1=2m/s2. The radius of the circle described is 4 m. The particle is initially at rest. Time after which total acceleration of the particle makes 45∘ with radial acceleration is :
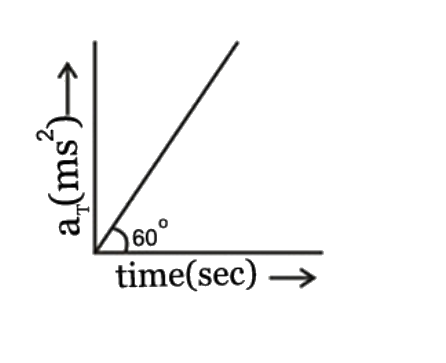
View SolutionTangental acceleration of a particle moving in a circle of radius 1 m varies with time t as shown in figure (initial velocity of the particle is zero). Time after which total acceleration of particle makes an angle of 30∘ with radial acceleration is
View SolutionStarting from rest, the acceleration of a particle is a=2(t-1). The velocity of the particle at t=5s is :-
View SolutionMotion of particle is given by equation
s=(5t3+3t2+8t+17)m
The value of acceleration of the particle at t = 2 s is
View SolutionIf a particle moves in a circle of radius of 4m at speed given by v=2t where v is in m/s and t in sec.At t=4s ,net accleration of particle will be:
View SolutionVelocity of a particle is given as v=(2t2−3)m/s. The acceleration of particle at t = 3s will be :
View SolutionIf s=et (sin t - cos t) is the equation of motion of a moving particle, then acceleration at time t is given by
View SolutionIn a non - uniform circular motaion the ratio of tangential to radial acceleration is (where, r= radius of circle, v= speed of the particle, α= angular acceleration)
View SolutionIs the acceleration of particle in uniform circular motion constant or vartiable?
View SolutionThe velocity time relation of a particle is given by v =(3t2−2t−1)m/s Calculate the position and acceleration of the particle when velocity of the particle is zero . Given the initial position of the particle is 5m .
View Solution
