A chance of magnitude 1.6×10−19C moving in a circle of radius 5 cm in a uniform magnetic field 0.5 T After applying E=0.15Vm−1 charge starts moving in a straight line mass of charge will be
23×10−20kg
43×10−20kg
63×10−20kg
13×10−20kg
The correct Answer is:B
To solve the problem step by step, we need to find the mass of a charge moving in a magnetic field and then transitioning to a straight line motion due to an electric field.
Step 1: Understand the Forces Acting on the Charge
When the charge is moving in a circle, the magnetic force acts as the centripetal force. The magnetic force FB can be expressed as:
FB=QVB
where:
- Q is the charge,
- V is the velocity of the charge,
- B is the magnetic field strength.
Step 2: Set Up the Centripetal Force Equation
The centripetal force FC required to keep the charge moving in a circle is given by:
FC=mv2r
where:
- m is the mass of the charge,
- v is the velocity,
- r is the radius of the circular path.
Step 3: Equate the Forces
Since the magnetic force provides the centripetal force, we can set them equal to each other:
QVB=mv2r
Step 4: Rearranging for Velocity
From the equation above, we can express the velocity V:
V=QBrm
Step 5: Introduce the Electric Field
When the electric field E is applied, the electric force FE acting on the charge is given by:
FE=EQ
For the charge to start moving in a straight line, the electric force must balance the magnetic force:
EQ=QVB
This simplifies to:
E=VB
Step 6: Substitute for Velocity
From the earlier expression for V:
E=QBrmB
This can be rearranged to find the mass m:
m=QB2rE
Step 7: Plug in the Values
Now, substituting the known values:
- Q=1.6×10−19C
- B=0.5T
- r=5cm=0.05m
- E=0.15V/m
Substituting these values into the equation:
m=(1.6×10−19)×(0.5)2×(0.05)0.15
Step 8: Calculate the Mass
Calculating the components:
B2=(0.5)2=0.25
Now substituting:
m=(1.6×10−19)×0.25×0.050.15
Calculating the numerator:
1.6×0.25×0.05=0.02×10−19
Now dividing by 0.15:
m=0.02×10−190.15=2×10−211.5=43×10−20
Final Answer
Thus, the mass of the charge is:
m=43×10−20kg
---
When the charge is moving in a circle, the magnetic force acts as the centripetal force. The magnetic force FB can be expressed as:
FB=QVB
where:
- Q is the charge,
- V is the velocity of the charge,
- B is the magnetic field strength.
The centripetal force FC required to keep the charge moving in a circle is given by:
FC=mv2r
where:
- m is the mass of the charge,
- v is the velocity,
- r is the radius of the circular path.
Since the magnetic force provides the centripetal force, we can set them equal to each other:
QVB=mv2r
From the equation above, we can express the velocity V:
V=QBrm
When the electric field E is applied, the electric force FE acting on the charge is given by:
FE=EQ
For the charge to start moving in a straight line, the electric force must balance the magnetic force:
EQ=QVB
This simplifies to:
E=VB
From the earlier expression for V:
E=QBrmB
This can be rearranged to find the mass m:
m=QB2rE
Now, substituting the known values:
- Q=1.6×10−19C
- B=0.5T
- r=5cm=0.05m
- E=0.15V/m
m=(1.6×10−19)×(0.5)2×(0.05)0.15
Calculating the components:
B2=(0.5)2=0.25
Now substituting:
m=(1.6×10−19)×0.25×0.050.15
Calculating the numerator:
1.6×0.25×0.05=0.02×10−19
Now dividing by 0.15:
m=0.02×10−190.15=2×10−211.5=43×10−20
Thus, the mass of the charge is:
m=43×10−20kg
Similar Questions
A particle having the same charge as of electron moves in a circular path of radius 0.5 cm under the influence of a magnetic field of 0.5 T. If an electric field of 100V/m makes it to move in a straight path, then the mass of the particle is ( Given charge of electron =1.6×10−19C)
View SolutionA particle moves in a circle of diamater 1.0 cm under the action of magnetic field of 0.40 T, An electric field of 200Vm−1 makes the path straight. Find the charges/mass ratio of the particle.
View SolutionA charged particle of charge 1 mC and mass 2g is moving with a speed of 5m/s in a uniform magnetic field of 0.5 tesla. Find the maximum acceleration of the charged particle
View SolutionA charged particle of charge 1 mC and mass 2g is moving with a speed of 5m/s in a uniform magnetic field of 0.5 tesla. Find the maximum acceleration of the charged particle
View SolutionAs a charged particle 'q' moving with a velocity →v enters a uniform magnetic field →B, it experience a force →F=q(→v×→B).Forθ=0∘or180∘,θ being the angle between →vand→B, force experienced is zero and the particle passes undeflected. For θ=90∘, the particle moves along a circular arc and the magnetic force (qvB) provides the necessary centripetal force (mv2/r). For other values of θ(θ≠0∘,180∘,90∘), the charged particle moves along a helical path which is the resultant motion of simultaneous circular and translational motions.
Suppose a particle that carries a charge of magnitude q and has a mass 4×10−15 kg is moving in a region containing a uniform magnetic field →B=−0.4ˆkT. At some instant, velocity of the particle is →v=(8ˆi−6ˆj4ˆk)×106ms−1 and force acting on it has a magnitude 1.6 N
If the coordinates of the particle at t = 0 are (2 m, 1 m, 0), coordinates at a time t = 3 T, where T is the time period of circular component of motion. will be (take π=3.14)
View SolutionA particle having a charge of 10.0μC and mass 1μg moves in a circle of radius 10 cm under the influence of a magnetic field of induction 0.1T. When the particle is at a point P, a uniform electric field is switched on so that the particle starts moving along the tangent with a uniform velocity. The electric field is
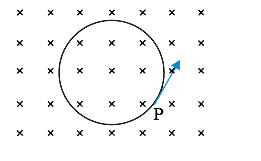
View SolutionAnswer the following:
a) Obtain the expression for the deflecting torque acting on the current carrying rectangular coil of a Galvanometer in a uniform magnetic field. Why is a radial magnetic field employed in the moving coil galvanometer?
b) Particles of mass 1.6×10−27 kg and charge 1.6×10−19 C are accelerated in a cyclotron of dee radius 40 cm. It employs a magnetic field of 0.4T. Find the kinetic energy (in MeV) of the particle beam imparted by the accelerator.
View SolutionAn electron (q=1.6×10−19C) is moving at right angles to a uniform magnetic field of 3.534×10−5 T The time taken by the electron to complete a circular orbit is
View SolutionA semicircular ring of radius 0.5 m is uniformly charged with a total charge of 1.5×10−9 coul. The electric potential at the centre of this ring is :
View SolutionA charge of 10−6C is describing a circular path of radius 1cm making 5 revolution per second. The magnetic induction field at the centre of the circle is
View Solution
