The relation between length L and radius R of the cylinder , if its moment of inertia about its axis is equal to that about the equatorial axis, will be
L = R
L = 2R
L = 3R
L=√3R
The correct Answer is:D
To find the relation between the length L and radius R of a cylinder when its moment of inertia about its axis is equal to that about the equatorial axis, we can follow these steps:
Step 1: Write the moment of inertia about the axis of the cylinder
The moment of inertia I1 of a solid cylinder about its own axis is given by the formula:
I1=12mR2
where m is the mass of the cylinder and R is its radius.
Step 2: Write the moment of inertia about the equatorial axis
The moment of inertia I2 of a solid cylinder about an axis through its center and perpendicular to its length (equatorial axis) can be calculated using the parallel axis theorem:
I2=112mL2+mR2
Here, L is the length of the cylinder.
Step 3: Set the two moments of inertia equal
According to the problem, we have:
I1=I2
Substituting the expressions we found:
12mR2=112mL2+mR2
Step 4: Simplify the equation
We can cancel m from both sides (assuming m≠0):
12R2=112L2+R2
Now, rearranging gives:
12R2−R2=112L2
This simplifies to:
−12R2=112L2
Step 5: Multiply through by -1
To make the equation easier to work with, multiply both sides by -1:
12R2=−112L2
Step 6: Clear fractions by multiplying by 12
Multiply through by 12 to eliminate the fractions:
6R2=−L2
Step 7: Rearranging and solving for L
Rearranging gives:
L2=6R2
Taking the square root of both sides results in:
L=√6R
Conclusion
Thus, the relation between the length L and radius R of the cylinder is:
L=√6R
The moment of inertia I1 of a solid cylinder about its own axis is given by the formula:
I1=12mR2
where m is the mass of the cylinder and R is its radius.
The moment of inertia I2 of a solid cylinder about an axis through its center and perpendicular to its length (equatorial axis) can be calculated using the parallel axis theorem:
I2=112mL2+mR2
Here, L is the length of the cylinder.
According to the problem, we have:
I1=I2
Substituting the expressions we found:
12mR2=112mL2+mR2
We can cancel m from both sides (assuming m≠0):
12R2=112L2+R2
Now, rearranging gives:
12R2−R2=112L2
This simplifies to:
−12R2=112L2
To make the equation easier to work with, multiply both sides by -1:
12R2=−112L2
Multiply through by 12 to eliminate the fractions:
6R2=−L2
Rearranging gives:
L2=6R2
Taking the square root of both sides results in:
L=√6R
Thus, the relation between the length L and radius R of the cylinder is:
L=√6R
Similar Questions
A circular disc of radius R and thickness R6 has moment of inertia I about its axis. If it is melted and casted into a solid sphere then what will be its moment of inertia, about its diametric axis?
View SolutionA uniform disc of radius R lies in the x−y plane, with its centre at origin. Its moment of inertia about z-axis is equal to its moment of inertia about line y=x+c. The value of c will be.
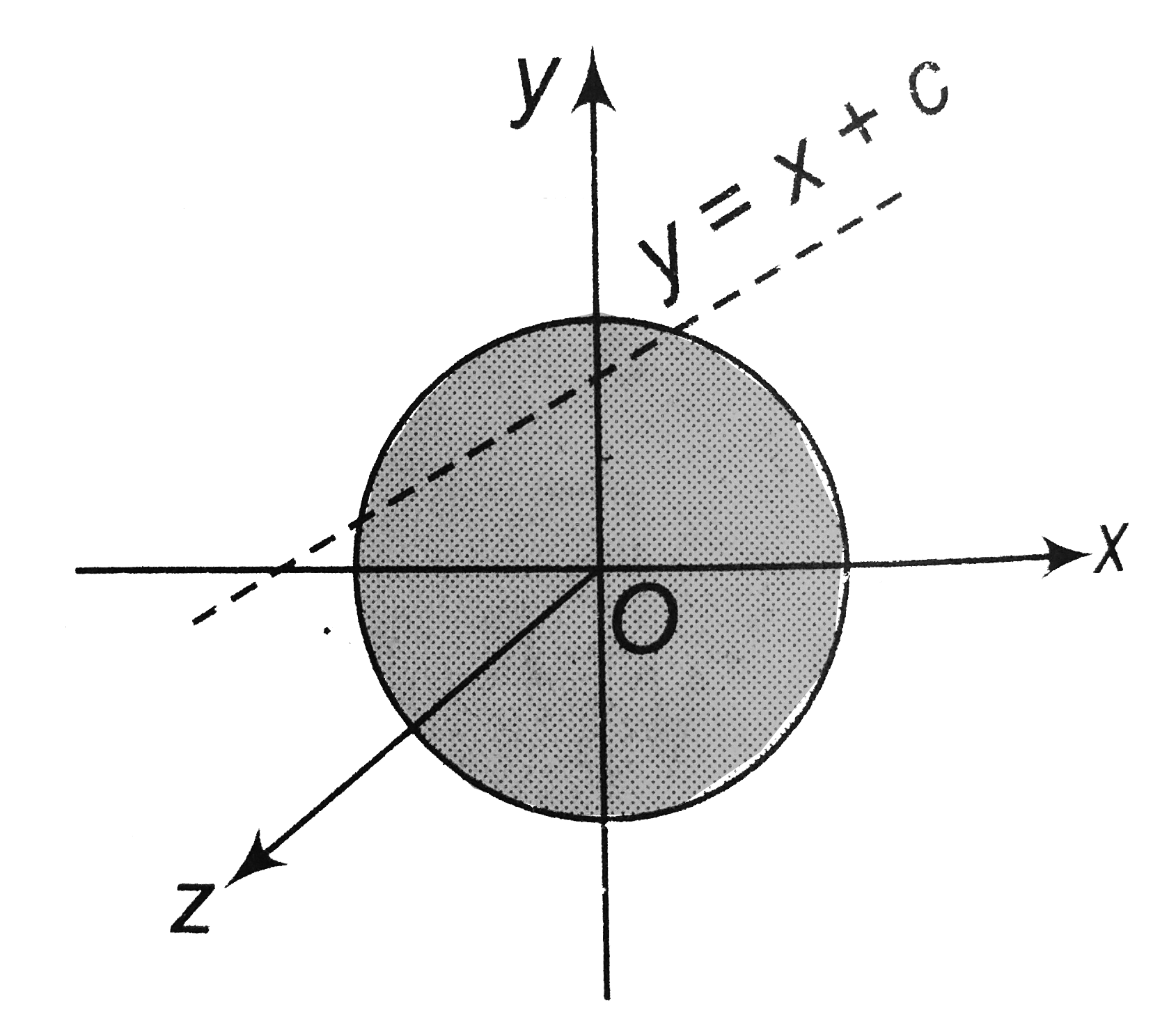 .
.
View Solution
Knowledge Check
A thin wire of length l and mass m is bent in the form of a semicircle as shown in the figure. Its moment of inertia about an axis joining its free ends will be
 Aml2BzeroCml2π2Dml22π2
Aml2BzeroCml2π2Dml22π2
A uniform disc of radius R lies in x-y plane with its centre at origin. Its moment of inertia about the axis x=2R and y=0 is equal to the moment of inertia about the axis y=d and z=0, where d is equal to
View SolutionThe moment of inertia of a ring about its geometrical axis is I, then its moment of inertia about its diameter will be
View SolutionThe diagram shows a uniform disc of mass M & radius 'a', if the moment of inertia of the disc about the axis XY is I, its moment of inertia about an axis through O and perpendicular to the plane of the disc is

View SolutionThe moment of inertia of thin uniform circular disc about one of the diameter is I. Its moment of inertia about an axis perpendicular to the circular surface and passing through its centre is
View SolutionWhat is moment of inertia of a cylinder of radius r, along its height?
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be

View SolutionA thin wire of length l and mass m is bent in the form of a semicircle as shown in the figure. Its moment of inertia about an axis joining its free ends will be

View Solution
