In a potentiometer experiment if the voltage across resistance R and R + r are balanced at the length l1andl2 respectively the value of resistance r will be
(l1−l2l2)R
(l1−l2l1)R
(l2−l1l1)R
(l2−l1l2)R
The correct Answer is:C
To solve the problem step by step, we will use the principles of a potentiometer and the relationships between voltage, resistance, and length.
1. Understanding the Potentiometer Principle:
In a potentiometer, the potential difference (voltage) across a length of wire is directly proportional to the length of the wire. This can be expressed as:
V=k⋅L
where V is the voltage, k is a constant (proportionality constant), and L is the length of the wire.
2. Setting Up the Equations:
For the first balance at length l1 with resistance R:
V=k⋅l1(1)
For the second balance at length l2 with resistance R+r:
V′=k⋅l2(2)
3. Relating Voltage to Resistance:
According to Ohm's law, the voltage across a resistor can also be expressed as:
V=I⋅RandV′=I′⋅(R+r)
where I and I′ are the currents through the resistors R and R+r, respectively.
4. Equating the Two Voltages:
Since both equations (1) and (2) represent the same potential difference, we can equate them:
k⋅l1=I⋅Randk⋅l2=I′⋅(R+r)
5. Finding the Wavelength:
From the first equation, we can express k:
k=Vl1=I⋅Rl1
Substituting k in the second equation:
I⋅Rl1⋅l2=I′⋅(R+r)
6. Subtracting the Equations:
Rearranging gives:
I⋅R⋅l2l1=I′⋅(R+r)
By subtracting the first equation from the second, we can isolate r:
(R+r)−R=I⋅Rl1⋅(l2−l1)
Thus,
r=I⋅Rl1⋅(l2−l1)
7. Final Expression for Resistance r:
We can express r in terms of R, l1, and l2:
r=Rl1⋅(l2−l1)
Conclusion:
The value of resistance r can be expressed as:
r=R⋅(l2−l1)l1
In a potentiometer, the potential difference (voltage) across a length of wire is directly proportional to the length of the wire. This can be expressed as:
V=k⋅L
where V is the voltage, k is a constant (proportionality constant), and L is the length of the wire.
For the first balance at length l1 with resistance R:
V=k⋅l1(1)
For the second balance at length l2 with resistance R+r:
V′=k⋅l2(2)
According to Ohm's law, the voltage across a resistor can also be expressed as:
V=I⋅RandV′=I′⋅(R+r)
where I and I′ are the currents through the resistors R and R+r, respectively.
Since both equations (1) and (2) represent the same potential difference, we can equate them:
k⋅l1=I⋅Randk⋅l2=I′⋅(R+r)
From the first equation, we can express k:
k=Vl1=I⋅Rl1
Substituting k in the second equation:
I⋅Rl1⋅l2=I′⋅(R+r)
Rearranging gives:
I⋅R⋅l2l1=I′⋅(R+r)
By subtracting the first equation from the second, we can isolate r:
(R+r)−R=I⋅Rl1⋅(l2−l1)
Thus,
r=I⋅Rl1⋅(l2−l1)
We can express r in terms of R, l1, and l2:
r=Rl1⋅(l2−l1)
The value of resistance r can be expressed as:
r=R⋅(l2−l1)l1
Similar Questions
In a series resonant circuit, the ac, voltage across resistance R, inductance L and capacitance are 5V, 10V and 10V, respectively. The ac. voltage applied to the circuit will be
View SolutionIn an LCR series ac circuit the voltage across L,C and R are V1,V2 and V3 respectively The voltage of the source is .
View Solution
Knowledge Check
AB is wire of potentiometer with the increase in the value of resistance R, the shift in the balance point J will be
 Atoward BBtoward ACremains constantDfirst towards B then back towards A
Atoward BBtoward ACremains constantDfirst towards B then back towards A
In an L-C-R circuit the AC voltage across R, L and C comes out as 10 V , 10 V and 20 V respectively . The voltage across the enter combination will be
View SolutionIf in a meter bridge experiment, the balancing length l was 25 cm for the situation shown in the figure. If the length and diameter of the of wire of resistance R is made half, then find the new balancing length in centimetre is
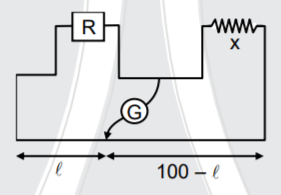
View SolutionIf in a meter bridge experiment, the balancing length l was 25 cm for the situation shown in the figure. If the length and diameter of the of wire of resistance R is made half, then find the new balancing length in centimetre is

View SolutionIn a potentiometer experiment, the balancing length with a resistance of 2Ω is found to be 100cm, while that of an unknown resistance is 500cm. Calculate the value of the unknown resistance.
View Solution
A uniform potentiometer wire AB of length 100 cm has a resistance of 5Ω and it is connected in series with an external resistance R and a cell of emf 6 V and negligible internal resistance. If a source of potential drop 2 V is balanced against a length of 60 cm of the potentiometer wire, the value of resistance R is
View SolutionIn a series L-C-R circuit the voltage across resistance , capacitance and inductance is 10 V each. If the capacitance is short circuited, the voltage across the inductance will be
View SolutionIf the resistance of potentiometer wire is 15r then calculate the balance length l
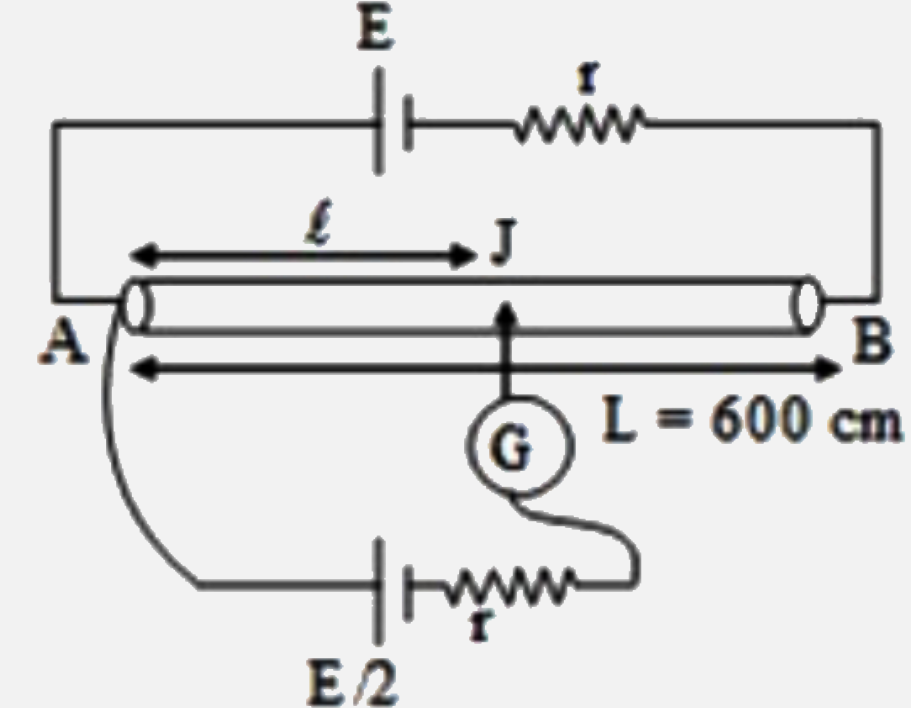
View Solution
