A conductor of resistance is stretched uniformly till its length if doubled. The wire is now bent in the form of an equivalent triangle. The effective resistance between the ends of any side of the triangle in ohm is
2
1
The correct Answer is:B
To solve the problem step by step, we will follow these steps:
Step 1: Understand the initial conditions
We have a conductor with an initial resistance R=3Ω. When the conductor is stretched uniformly, its length is doubled.
Step 2: Determine the new resistance after stretching
When the length of the conductor is doubled, the cross-sectional area A will decrease. Since the volume of the conductor remains constant, we can use the relationship:
Volume=Length×Area
Let the original length be L and the original area be A. The new length is 2L and the new area A′ can be calculated as:
L⋅A=2L⋅A′⟹A′=A2
Step 3: Calculate the new resistance
The resistance R′ of the conductor can be calculated using the formula:
R′=ρL′A′
Substituting the new length and area:
R′=ρ2LA/2=ρ4LA=4R
Since the original resistance R=3Ω:
R′=4×3Ω=12Ω
Step 4: Form the equilateral triangle
Now, the wire with resistance 12Ω is bent into the form of an equilateral triangle. Each side of the triangle will have equal resistance. Since the total length of the wire is now 2L, and it is divided into 3 equal sides, the resistance of each side Rside is:
Rside=R′3=12Ω3=4Ω
Step 5: Calculate the effective resistance between two points
To find the effective resistance between the ends of any side of the triangle, we note that when measuring between two vertices of the triangle, we have two resistors of 4Ω in parallel (the two other sides of the triangle). The formula for the equivalent resistance Req of two resistors R1 and R2 in parallel is given by:
1Req=1R1+1R2
Substituting R1=R2=4Ω:
1Req=14+14=24=12
Thus,
Req=2Ω
Final Answer
The effective resistance between the ends of any side of the triangle is 2Ω.
---
We have a conductor with an initial resistance R=3Ω. When the conductor is stretched uniformly, its length is doubled.
When the length of the conductor is doubled, the cross-sectional area A will decrease. Since the volume of the conductor remains constant, we can use the relationship:
Volume=Length×Area
Let the original length be L and the original area be A. The new length is 2L and the new area A′ can be calculated as:
L⋅A=2L⋅A′⟹A′=A2
The resistance R′ of the conductor can be calculated using the formula:
R′=ρL′A′
Substituting the new length and area:
R′=ρ2LA/2=ρ4LA=4R
Since the original resistance R=3Ω:
R′=4×3Ω=12Ω
Now, the wire with resistance 12Ω is bent into the form of an equilateral triangle. Each side of the triangle will have equal resistance. Since the total length of the wire is now 2L, and it is divided into 3 equal sides, the resistance of each side Rside is:
Rside=R′3=12Ω3=4Ω
To find the effective resistance between the ends of any side of the triangle, we note that when measuring between two vertices of the triangle, we have two resistors of 4Ω in parallel (the two other sides of the triangle). The formula for the equivalent resistance Req of two resistors R1 and R2 in parallel is given by:
1Req=1R1+1R2
Substituting R1=R2=4Ω:
1Req=14+14=24=12
Thus,
Req=2Ω
The effective resistance between the ends of any side of the triangle is 2Ω.
Similar Questions
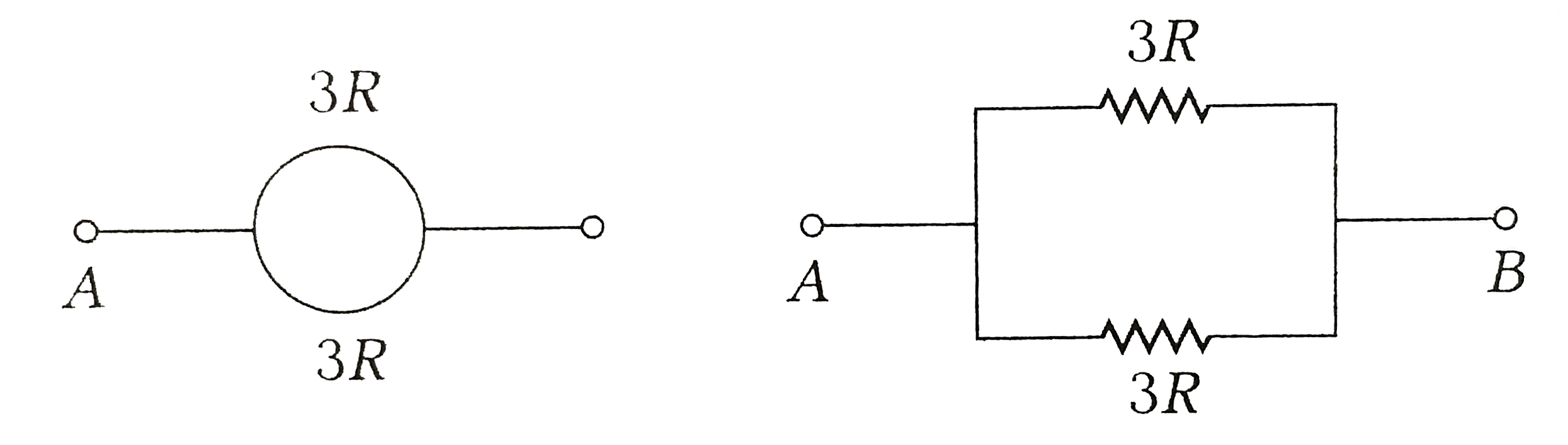
A wire of resistance 8R is bent in the form of a circle. What is the effective resistance between the ends of a diameter AB?
View SolutionA wire has a resistance of 12 ohm . It is bent in the form of equilateral triangle. The effective resistance between any two corners of the triangle is
View Solution
Knowledge Check
A uniform wire of resistance 36Ω is bent in the form of a circle. The effective resistance across the points A and B is
 A5ΩB15ΩC7.2ΩD30Ω
A5ΩB15ΩC7.2ΩD30Ω
A wire of resistance 6R is bent in the form of a circle. What is the effective resistance between the ends of the diameter?
View SolutionA uniform wire is bent in the form of a circle as shown in the figure. The effective resistance between A and B is maximum if theta is
_PHY_E01_003_Q01.png)
View SolutionA wire is bent in the form of a triangle now the equivalent resistance between its one end and the mid point of the side is
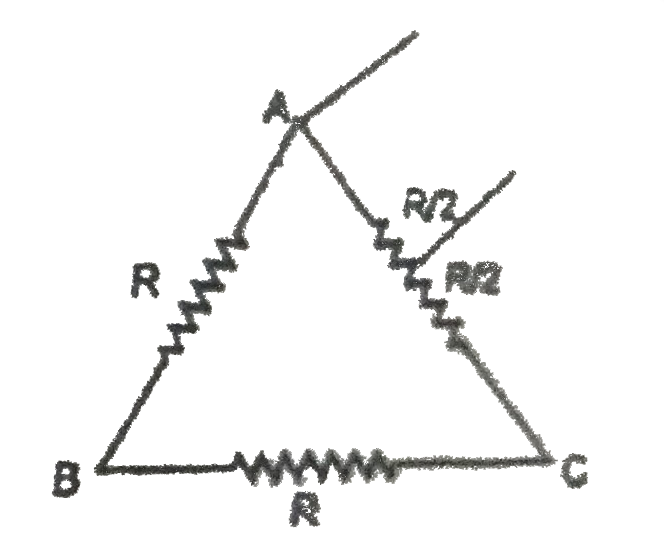
View SolutionThe resistance of each side of an equilateral triangle is 6 ohm. Calculate the equivalent resistance between ends of a side.
View SolutionA wire has resistance 12Ω. It is bent in the form of a circle. The effective resistance between two points across a diameter is.
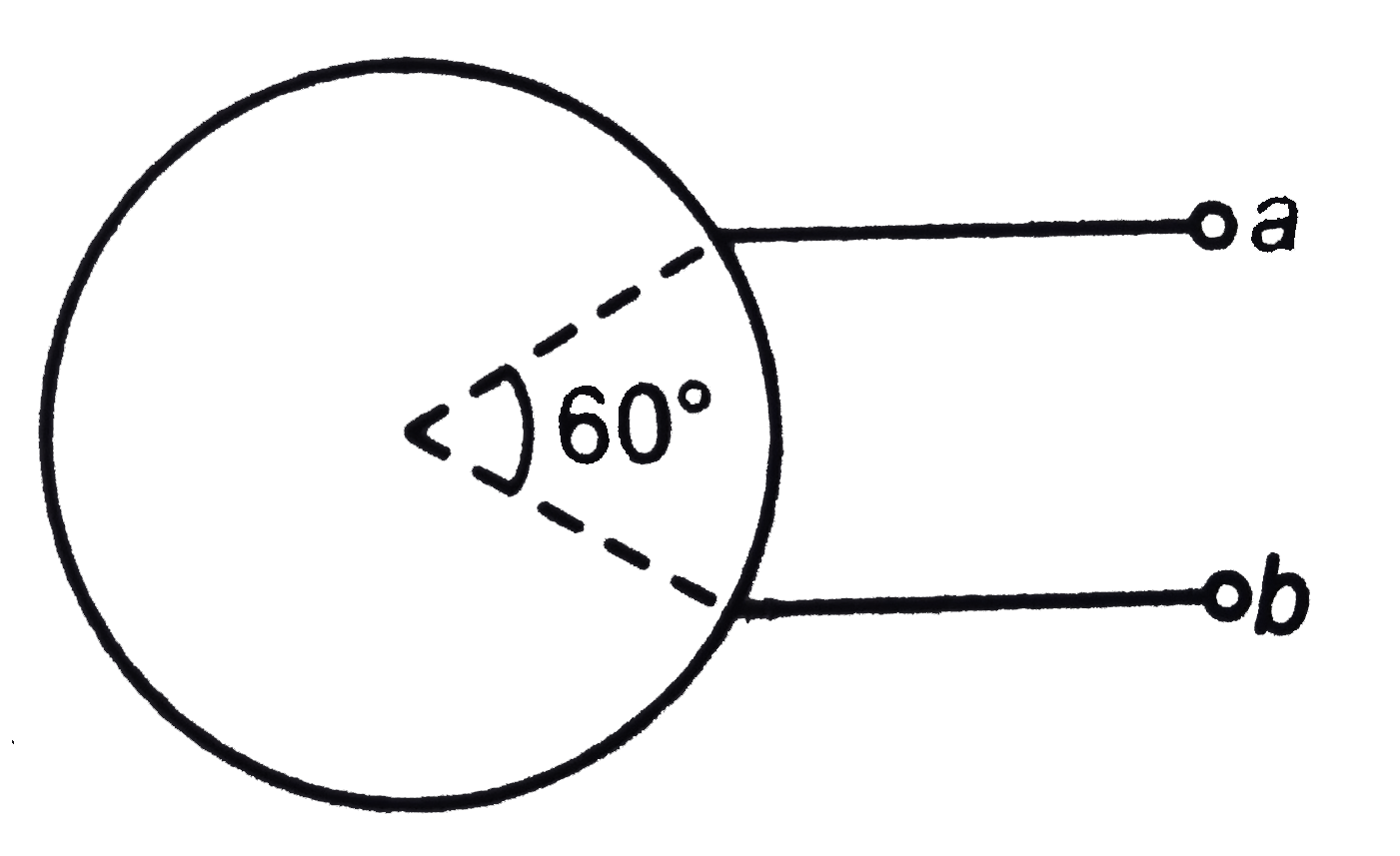
View SolutionA uniform wire of resistance 18Ω is bent in the form of a circle. The effective resistance across the points a and b is
View SolutionA wire has resistance of 24Ω is bent in the following shape. The effective resistance between A and B is
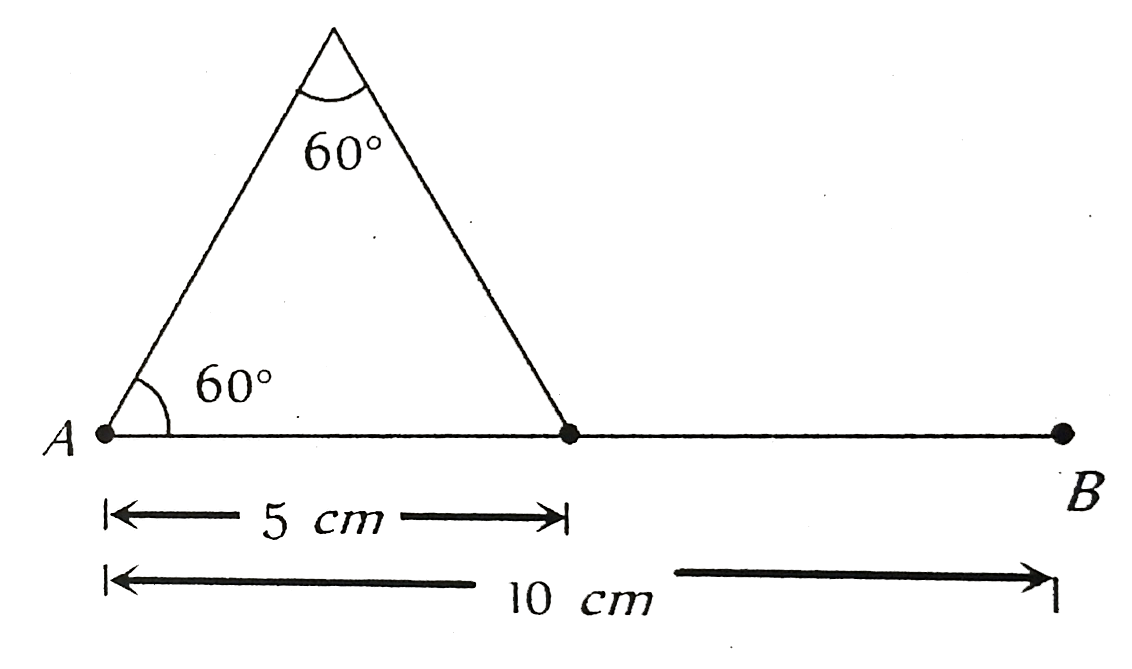
View Solution
