A wire has a resistance of 12 ohm . It is bent in the form of equilateral triangle. The effective resistance between any two corners of the triangle is
6Ω
83Ω
9Ω
12Ω
The correct Answer is:B
To solve the problem of finding the effective resistance between any two corners of a wire bent in the form of an equilateral triangle, we can follow these steps:
Step 1: Determine the total resistance of the wire
The total resistance of the wire is given as R0=12Ω.
Step 2: Calculate the length of each side of the triangle
Since the wire is bent into the shape of an equilateral triangle, the total length of the wire is divided into three equal parts. Therefore, the length of each side of the triangle is:
L=Ltotal3
The resistance of each side of the triangle can be calculated using the formula for resistance:
Rside=R03=12Ω3=4Ω
Step 3: Draw the circuit
Label the corners of the triangle as A, B, and C. The resistances between the corners are:
- RAB=4Ω (between A and B)
- RAC=4Ω (between A and C)
- RBC=4Ω (between B and C)
Step 4: Analyze the circuit between two corners
To find the effective resistance between points A and B, we can see that:
- RAC and RBC are in series with each other.
- Therefore, the total resistance of the path from A to C to B is:
RAC+RBC=4Ω+4Ω=8Ω
Step 5: Combine the resistances in parallel
Now, we have two paths between A and B:
1. Directly through RAB=4Ω
2. Through RAC and RBC which totals to 8Ω
These two resistances are in parallel. The formula for equivalent resistance RAB for two resistors in parallel R1 and R2 is given by:
1RAB=1R1+1R2
Substituting the values:
1RAB=14Ω+18Ω
Step 6: Calculate the equivalent resistance
Calculating the right-hand side:
1RAB=28+18=38
Thus,
RAB=83Ω
Conclusion
The effective resistance between any two corners of the triangle is:
RAB=83Ω
The total resistance of the wire is given as R0=12Ω.
Since the wire is bent into the shape of an equilateral triangle, the total length of the wire is divided into three equal parts. Therefore, the length of each side of the triangle is:
L=Ltotal3
The resistance of each side of the triangle can be calculated using the formula for resistance:
Rside=R03=12Ω3=4Ω
Label the corners of the triangle as A, B, and C. The resistances between the corners are:
- RAB=4Ω (between A and B)
- RAC=4Ω (between A and C)
- RBC=4Ω (between B and C)
To find the effective resistance between points A and B, we can see that:
- RAC and RBC are in series with each other.
- Therefore, the total resistance of the path from A to C to B is:
RAC+RBC=4Ω+4Ω=8Ω
Now, we have two paths between A and B:
1. Directly through RAB=4Ω
2. Through RAC and RBC which totals to 8Ω
1RAB=1R1+1R2
Substituting the values:
1RAB=14Ω+18Ω
Calculating the right-hand side:
1RAB=28+18=38
Thus,
RAB=83Ω
The effective resistance between any two corners of the triangle is:
RAB=83Ω
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Match the columns
4 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
A uniform metallic wire has a resistance of 18 Ω and is bent into an equiolateral triangle. Then, the resistance between any two vertices of the triangle is :
View SolutionA wire has resistance 12Ω. It is bent in the form of a circle. The effective resistance between two points across a diameter is.
View SolutionA wire has resistance of 24Ω is bent in the following shape. The effective resistance between A and B is
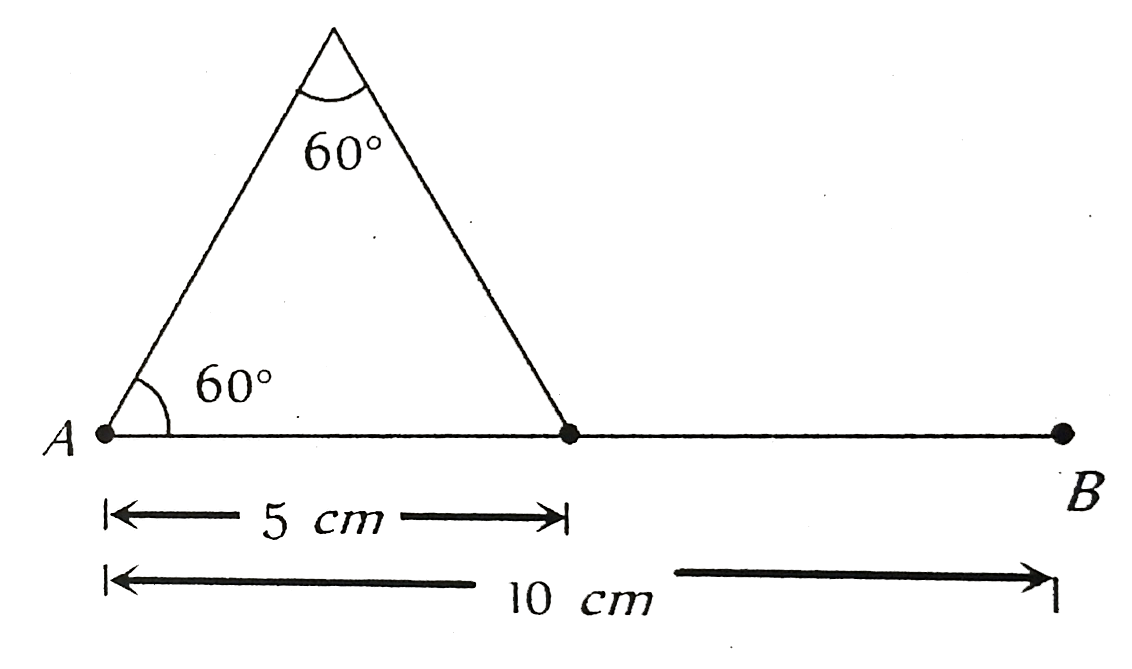
View SolutionA conductor of resistance 3Ω is stretched uniformly till its length if doubled. The wire is now bent in the form of an equivalent triangle. The effective resistance between the ends of any side of the triangle in ohm is
View SolutionA wire is bent in the form of a triangle now the equivalent resistance between its one end and the mid point of the side is
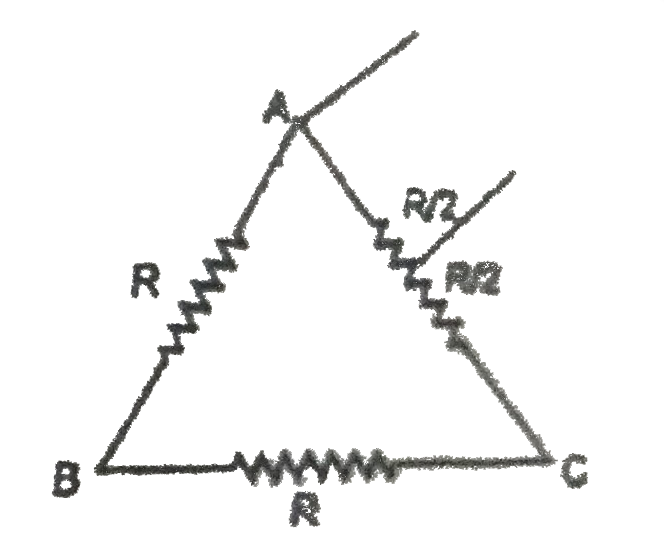
View SolutionA wire of resistance 8R is bent in the form of a circle. What is the effective resistance between the ends of a diameter AB?
View SolutionA wire of resistance 6R is bent in the form of a circle. What is the effective resistance between the ends of the diameter?
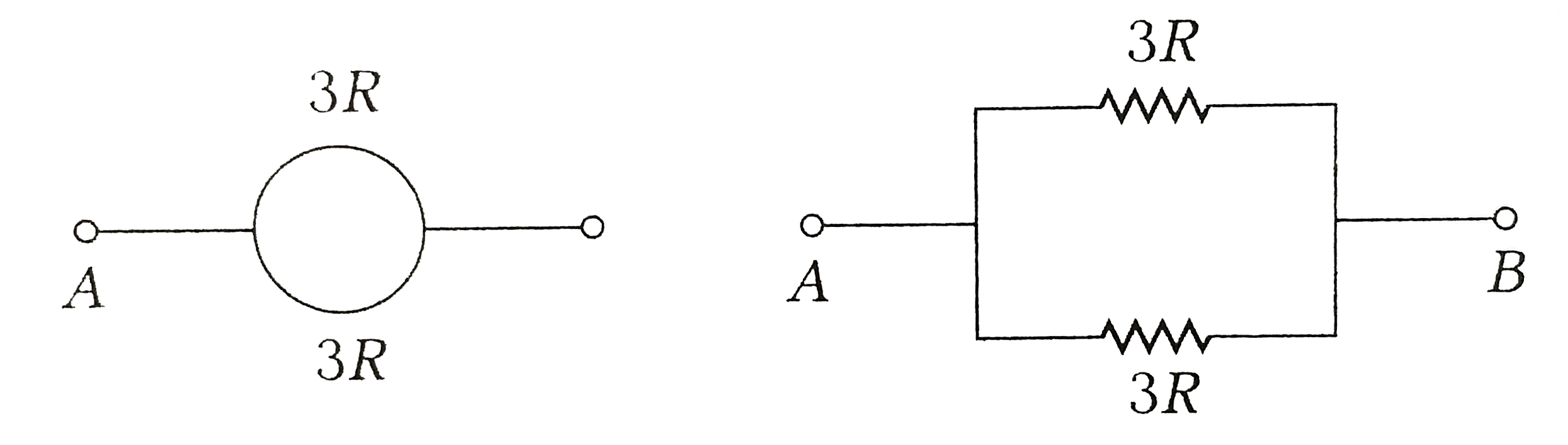
View SolutionA uniform wire of resistance 18Ω is bent in the form of a circle. The effective resistance across the points a and b is
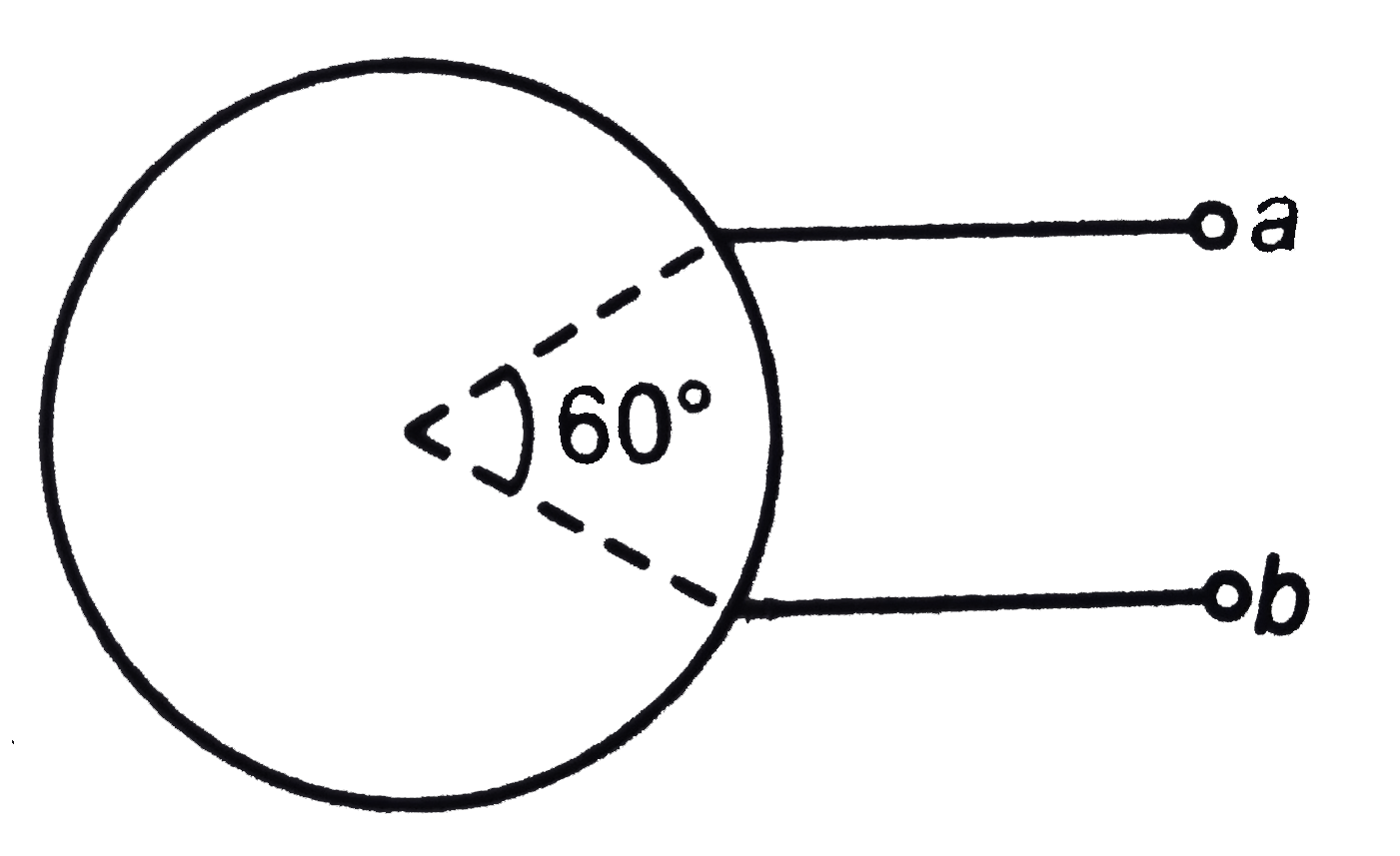
View SolutionIn the given network of resistances, the effective resistance between A and B is
View SolutionA uniform wire of resistance 36Ω is bent in the form of a circle. The Effective resistance between A and B is (O is the centre of circle):

View Solution
