A man of mass 60 kg climbed down using an elevator . The elevator had an acceleration of 4ms−2 . If the acceleration due to gravity is 10ms−2 , the man's apparent weight on his way down is
(a)60 N
(b)240 N
(c)360 N
(d)840 N
The correct Answer is:C
To find the man's apparent weight while he is descending in the elevator, we can follow these steps:
Step 1: Understand the Forces Acting on the Man
When the man is in the elevator, two main forces act on him:
1. The gravitational force acting downward, which is given by Fg=m⋅g.
2. The normal force acting upward, which we will denote as N.
Step 2: Identify the Given Values
- Mass of the man, m=60kg
- Acceleration of the elevator, a=4m/s2
- Acceleration due to gravity, g=10m/s2
Step 3: Write the Equation for Apparent Weight
When the elevator accelerates downward, the apparent weight N can be calculated using the following equation derived from Newton's second law:
N=m⋅(g−a)
This equation states that the normal force (apparent weight) is equal to the gravitational force minus the force due to the elevator's acceleration.
Step 4: Substitute the Values into the Equation
Now we can substitute the known values into the equation:
N=60kg⋅(10m/s2−4m/s2)
N=60kg⋅(6m/s2)
Step 5: Calculate the Apparent Weight
Now we can perform the multiplication:
N=60⋅6=360N
Conclusion
The man's apparent weight while descending in the elevator is 360N.
When the man is in the elevator, two main forces act on him:
1. The gravitational force acting downward, which is given by Fg=m⋅g.
2. The normal force acting upward, which we will denote as N.
- Mass of the man, m=60kg
- Acceleration of the elevator, a=4m/s2
- Acceleration due to gravity, g=10m/s2
When the elevator accelerates downward, the apparent weight N can be calculated using the following equation derived from Newton's second law:
N=m⋅(g−a)
This equation states that the normal force (apparent weight) is equal to the gravitational force minus the force due to the elevator's acceleration.
Now we can substitute the known values into the equation:
N=60kg⋅(10m/s2−4m/s2)
N=60kg⋅(6m/s2)
Now we can perform the multiplication:
N=60⋅6=360N
The man's apparent weight while descending in the elevator is 360N.
Similar Questions
Find the acceleration of 3kg mass when acceleration of 2kg mass is ms−2 as shwon in fig.
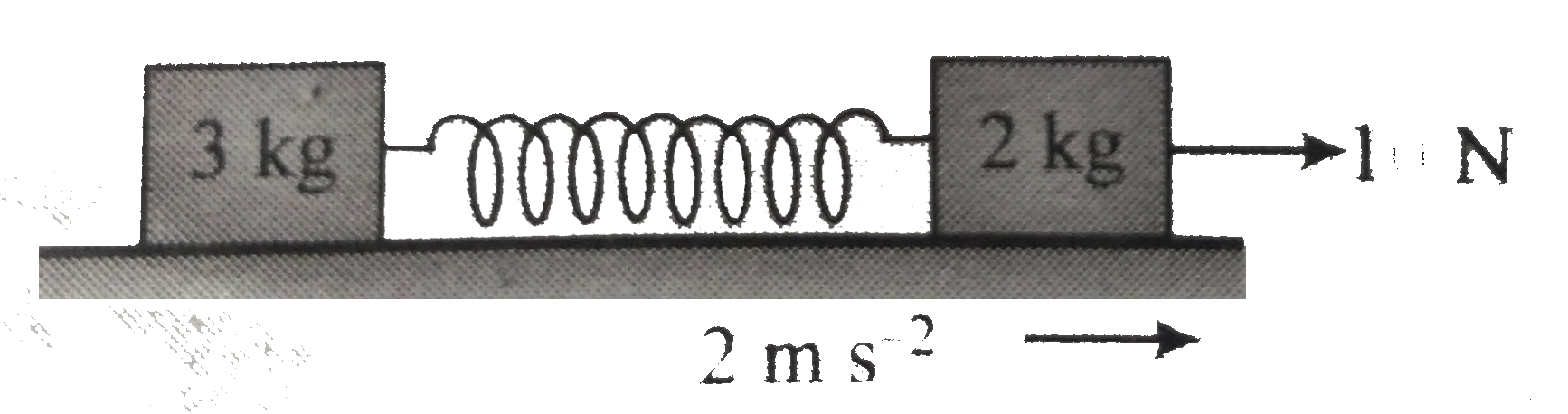
View SolutionA man of mass 60 kg is in a lift and lift is accelerating upwards with acceleration 4m/s2. Calculate effective weight of man in lift.
View SolutionA boy of mass 40 kg climbs up a rope with an acceleration of 2ms−2 . What is the tension in the rope ?
View SolutionFind the acceleration of 3 kg mass when acceleration of 2 kg mass is 2ms−2 as shown in figure-2.140
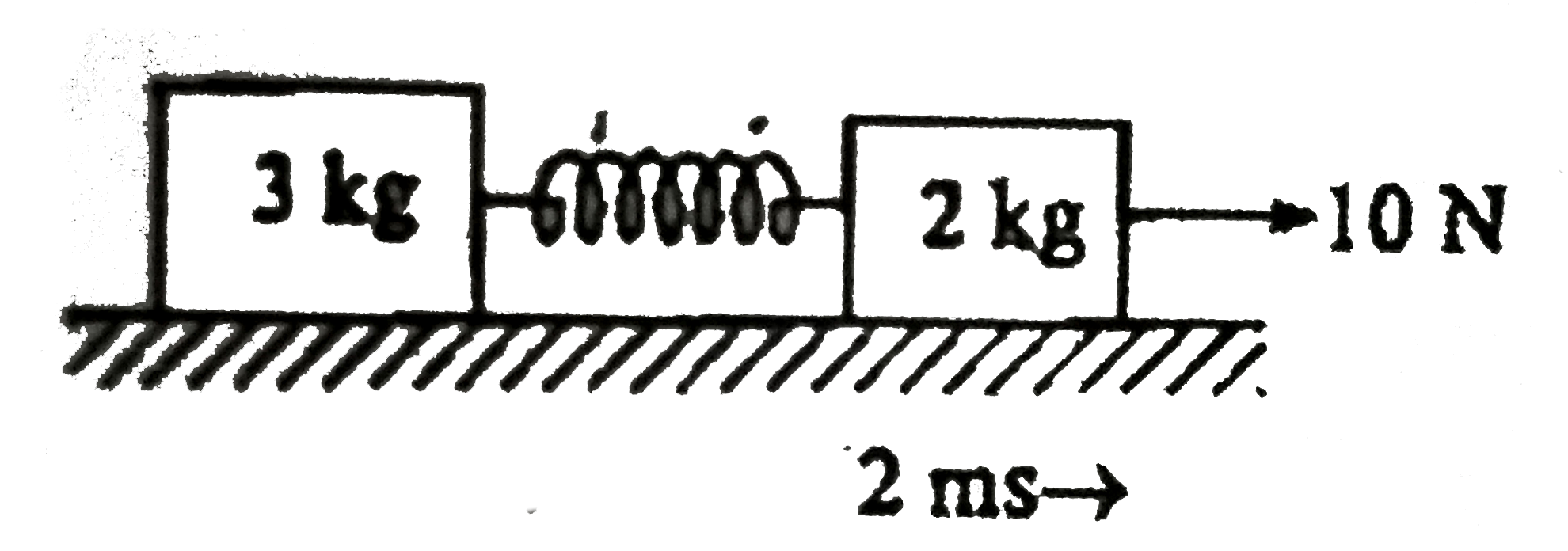
View SolutionA 60 kg man stands on an elevator floor The elevator is going up with constant acceleration of 1.96 m/s2. Percentage change in the apparent weight of the person is
View SolutionA man in a lift feels an apparent weight W when the lift is moving up with a uniform acceleration of 1/3rd of the acceleration due to gravity. If the same man were in the same lift now moving down with a uniform acceleration that is 1/2 of the acceleration due to gravity, then his apparent weight is
View SolutionAn elevator weighing 6000 kg is pulled upward by a cable with an acceleration of 5ms−2 . Taking g to be 10ms−2 , then the tension in the cable is
View SolutionThe friction of the air causes a vertical retardation equal to 10% of the acceleration due to gravity (takeg=10ms−2) The maximum height will be decreased by:
View SolutionA man of mass 60 kg is standing on a horizontal conveyor belt. When the belt is given an acceleration of 1ms−2, the man remains stationary with respect to the moving belt. If g=10ms−2, The net force acting on the man is

View SolutionA balloon of mass 10 kg is raising up with an acceleration of 20ms−2. If a mass of 4 kg is removed from the balloon its acceleration becomes ( take, g=10ms−2)
View Solution
