When connected across the terminals of a cell, a voltmeter measures 5 V and a connected ammeter measures 10 A of current. A resistance of 2 ohm s is connected across the terminals of the cell. The current flowing through this resistance will be
The correct Answer is:m(R−r)M+m,m√2g(R−r)M(M+m)
To solve the problem step by step, we will follow the principles of Ohm's law and the current division rule.
Step 1: Identify the given values
- Voltage (V) = 5 V
- Current (I) = 10 A
- Resistance (R) = 2 Ω (the resistance connected across the terminals of the cell)
Step 2: Calculate the internal resistance of the cell
Using Ohm's law, which states that V=I⋅R, we can find the internal resistance (R_internal) of the cell.
Rinternal=VI=5V10A=0.5Ω
Step 3: Determine the total resistance in the circuit
The internal resistance of the cell (0.5 Ω) and the external resistance (2 Ω) are in parallel. The formula for the equivalent resistance (R_eq) of two resistors in parallel is given by:
1Req=1Rinternal+1Rexternal
Substituting the values we have:
1Req=10.5+12
Calculating the right-hand side:
1Req=2+0.5=2.5
Now, taking the reciprocal to find R_eq:
Req=12.5=0.4Ω
Step 4: Calculate the total current through the circuit
The total current flowing through the circuit remains the same as measured, which is 10 A.
Step 5: Use the current division rule to find the current through the 2 Ω resistor
According to the current division rule, the current through the 2 Ω resistor (I_2) can be calculated as:
I2=I⋅RinternalRinternal+Rexternal
Substituting the values we have:
I2=10A⋅0.5Ω0.5Ω+2Ω
Calculating the denominator:
I2=10A⋅0.52.5=10A⋅0.2=2A
Final Answer
The current flowing through the 2 Ω resistor is 2 A.
---
- Voltage (V) = 5 V
- Current (I) = 10 A
- Resistance (R) = 2 Ω (the resistance connected across the terminals of the cell)
Using Ohm's law, which states that V=I⋅R, we can find the internal resistance (R_internal) of the cell.
The internal resistance of the cell (0.5 Ω) and the external resistance (2 Ω) are in parallel. The formula for the equivalent resistance (R_eq) of two resistors in parallel is given by:
The total current flowing through the circuit remains the same as measured, which is 10 A.
According to the current division rule, the current through the 2 Ω resistor (I_2) can be calculated as:
The current flowing through the 2 Ω resistor is 2 A.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-IV B14videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-V A20videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-III26videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)6videos
CIRCULAR MOTION
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective14videos
GEOMETRICAL OPTICS
Similar Questions
Resistors of 1, 2, 3 ohm are connected in the form of a triangle. If a 1.5V cell of negligible internal resistance is connected across 3 ohm resistor, the current flowing through this resistance will be
View SolutionA battery of emf 2 V and initial resistance 1Ω is
connected across terminals A and B of the circuit shown
in figure
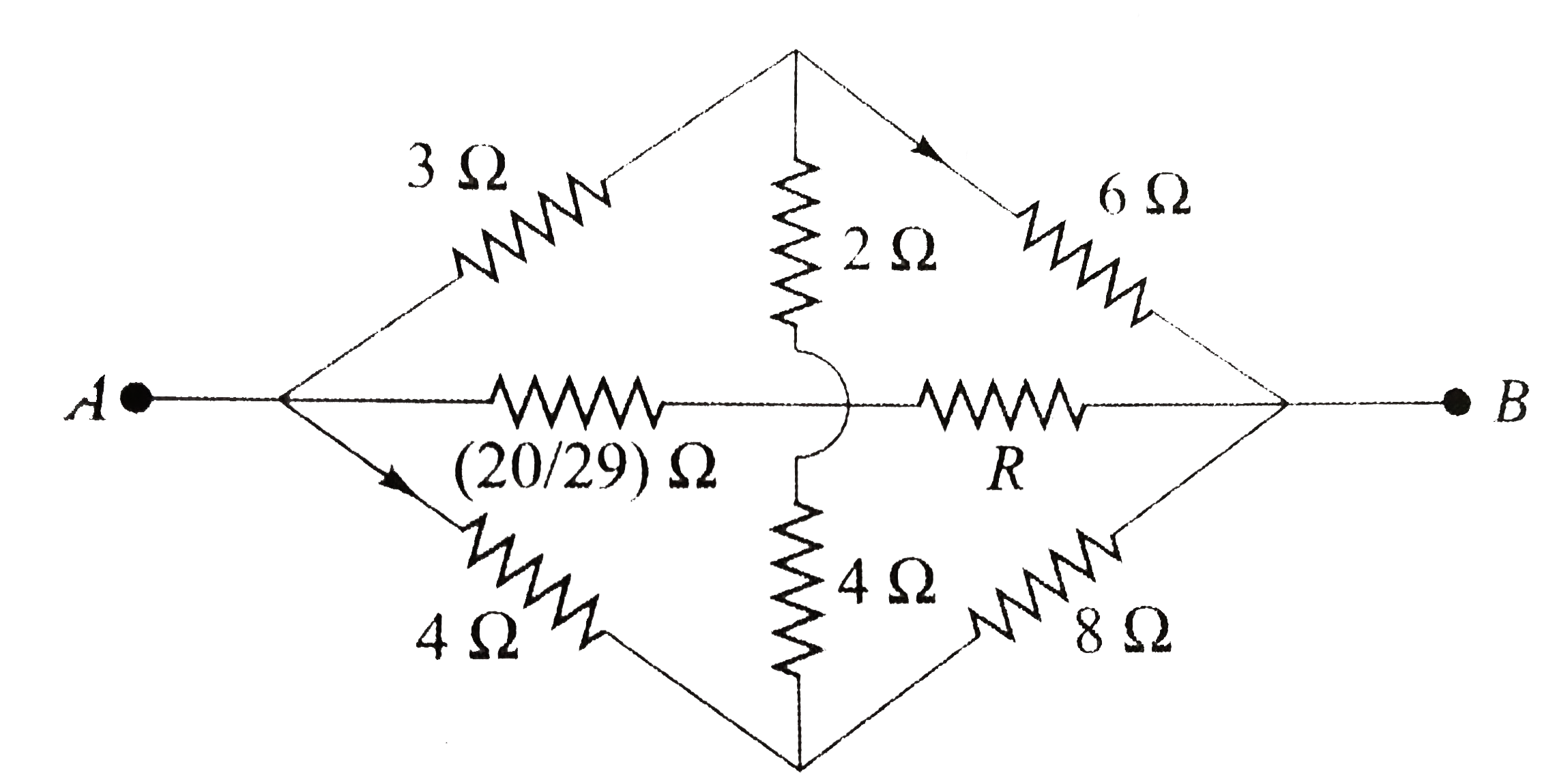 . View Solution
. View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance 1.5(Ω). Find the current flow through battery ?
View SolutionSix resistors, each of value3Ω are connected as shown in the figure. A cell of emf 3V is connected across AB. The effective resistance across AB and the current through the arm AB will be :
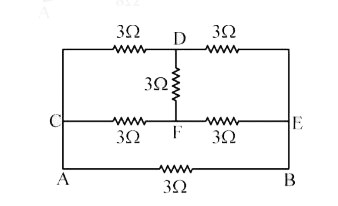 View Solution
View SolutionA 50V battery is connected across a 10 ohm resistor. The current is 4.5A is flowing through the resistor then the internal resistance of the battery is
View SolutionFind the current through the 10Ω resistance connected across AB
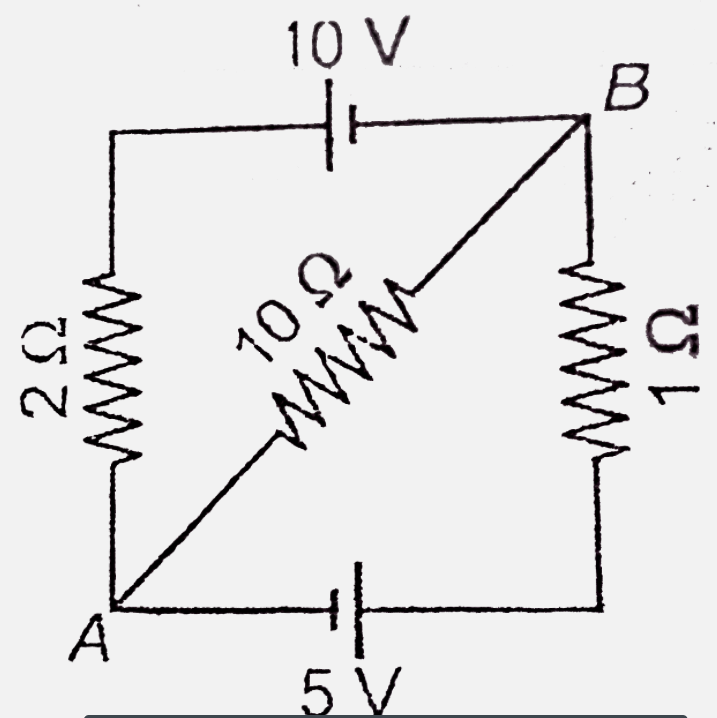 View Solution
View SolutionWrite any two factors on which internal resistance of a cell depends . The reading on a high resistance voltmeter , when a cell is connected across it , is 2.0 V . When the terminals of the cell are also connected to a resistance of 3Ω as shown in the circuit , the voltmeter reading drops to 1.5 V . Find the internal resistance of the cell.
View SolutionIn a potentiometer experiment it is found that no current passes through the galvanometer when the terminals of the cell are connected across 0.52m of the potentiometer wire. If the cell is shunted by a resistance of 5Ω balance is obtained when the cell connected across0.4m of the wire. Find the internal resistance of the cell.
View SolutionIn a potentiometer experiment it is found that no current passes through the galvanometer when the terminals of the cell are connected across 0.52m of the potentiometer wire. If the cell is shunted by a resistance of 5Ω balance is obtained when the cell connected across0.4m of the wire. Find the internal resistance of the cell.
View SolutionThe emf of a daniel cell is 1.08V. When the terminals of the cell are connected to resistance of 3Ω, the potential difference across the terminals is found to be 0.6 V. Then , the internal resistance of the cell is
View Solution

