A sphere of mass m is rolling without sliding along positive x-axis on a rough horizontal surface of coefficient of friction μ. It elastically collides with a wall and then returns. The correct statement of frictional force (f) acting on the sphere is
f=μmgˆi before collision and f=μmgˆi after collision
f=0 before collision and f=+μmgˆi after collision
f<μmgˆi before collision and f=μmgˆi after collision
f=μmgˆi before collision and just after collision
The correct Answer is:B
To solve the problem, we need to analyze the motion of the sphere before and after it collides with the wall. Here are the steps to arrive at the solution:
Step 1: Understand the Initial Motion of the Sphere
The sphere is rolling without sliding along the positive x-axis. This means that the center of mass of the sphere is moving in the positive x direction, while the point of contact with the ground is moving in the opposite direction (negative x direction).
Hint: Remember that for rolling without slipping, the velocity of the center of mass and the velocity of the point of contact have a specific relationship.
Step 2: Identify the Direction of Friction Force Before Collision
Since the bottom point of the sphere is moving in the negative x direction, the frictional force must act in the positive x direction to prevent slipping. This frictional force helps maintain the rolling motion.
Hint: Friction acts in the direction that opposes the relative motion between the surfaces in contact.
Step 3: Analyze the Collision with the Wall
When the sphere collides elastically with the wall, its velocity reverses direction. The center of mass will now move in the negative x direction immediately after the collision.
Hint: In an elastic collision, both momentum and kinetic energy are conserved.
Step 4: Determine the Direction of Friction Force After Collision
After the collision, the bottom point of the sphere is still rotating in the clockwise direction. Therefore, the bottom point is again moving in the negative x direction. The frictional force will still act in the positive x direction to maintain rolling without slipping.
Hint: The direction of friction depends on the motion of the point of contact relative to the surface.
Step 5: Calculate the Magnitude of the Frictional Force
The maximum static friction force can be calculated using the formula:
f=μ⋅N
where N is the normal force. For a sphere of mass m on a horizontal surface, the normal force N is equal to the weight of the sphere, mg. Therefore, the frictional force is:
f=μ⋅mg
Hint: The normal force is influenced by the weight of the object, which is important for calculating friction.
Step 6: Conclude the Result
Since the frictional force acts in the positive x direction both before and after the collision, we can summarize that:
- Before collision: f=μmg^i
- After collision: f=μmg^i
Thus, the correct statement is that the frictional force acting on the sphere is f=μmg^i both before and after the collision.
Final Answer: The correct statement is F=μmg^i before collision and F=μmg^i after collision.
The sphere is rolling without sliding along the positive x-axis. This means that the center of mass of the sphere is moving in the positive x direction, while the point of contact with the ground is moving in the opposite direction (negative x direction).
Since the bottom point of the sphere is moving in the negative x direction, the frictional force must act in the positive x direction to prevent slipping. This frictional force helps maintain the rolling motion.
When the sphere collides elastically with the wall, its velocity reverses direction. The center of mass will now move in the negative x direction immediately after the collision.
After the collision, the bottom point of the sphere is still rotating in the clockwise direction. Therefore, the bottom point is again moving in the negative x direction. The frictional force will still act in the positive x direction to maintain rolling without slipping.
The maximum static friction force can be calculated using the formula:
f=μ⋅N
where N is the normal force. For a sphere of mass m on a horizontal surface, the normal force N is equal to the weight of the sphere, mg. Therefore, the frictional force is:
f=μ⋅mg
Since the frictional force acts in the positive x direction both before and after the collision, we can summarize that:
- Before collision: f=μmg^i
- After collision: f=μmg^i
Similar Questions
A block of mass 10 kg is placed on a rough horizontal surface of coefficient of friction 0.1. A pulling force of 100 N acts on it at 37∘ with the horizontal. The frictional force acting on the body is ..... N.
View SolutionA massless string is wrapped around a hollow cylinder having mass m and radius r. The cylinder is kept on a rough horizontal surface (coefficient of friction is μ). A constant force F is applied as shown in the figure. In case of pure rolling, the friction force acting on the bottom most point of the cylinder is
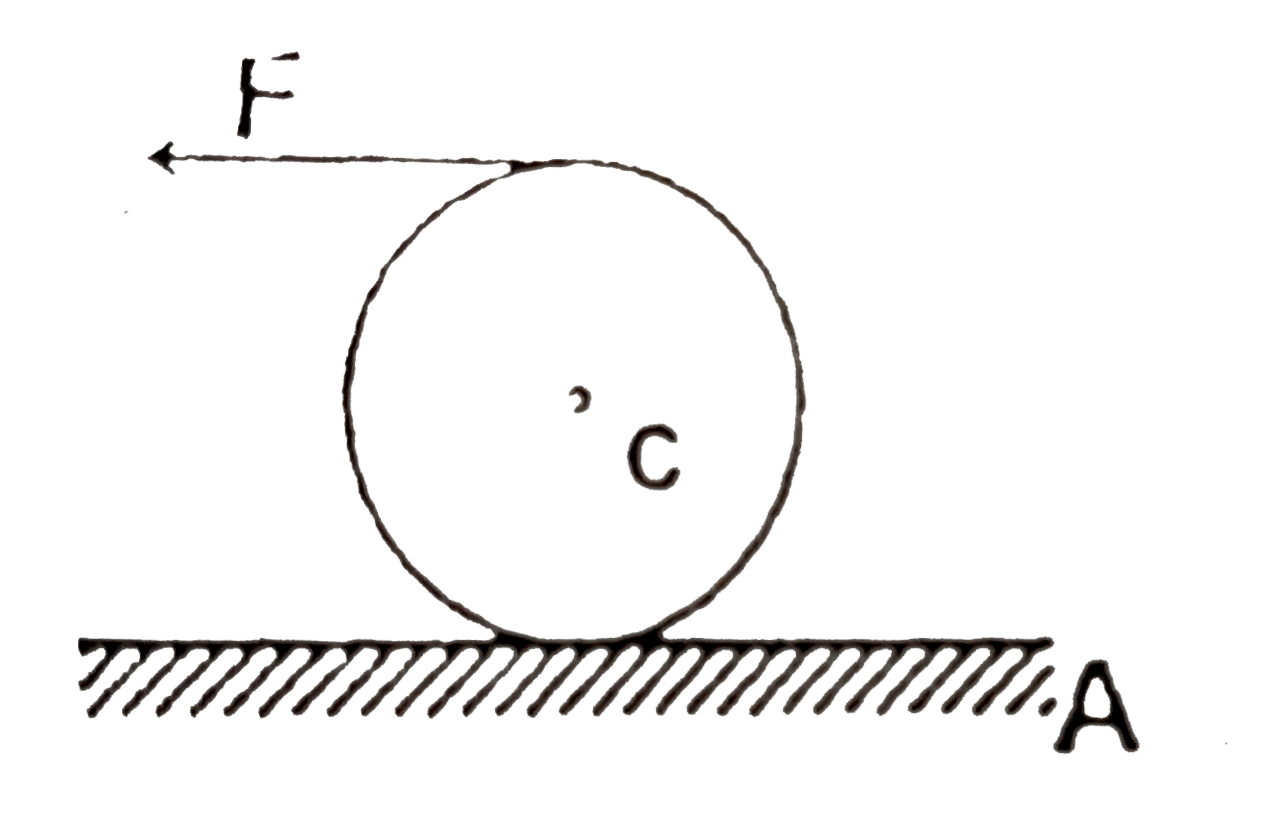
View Solution
A solid sphere is rolling purely on a rough horizontal surface (coefficient of kinetic friction =μ) with speed of centre =u. It collides inelastically with a smooth vertical wall at a certain moment, the coefficient of restituting being 12. The sphere will begin pure rolling after a time.
View SolutionA solid sphere of mass m is lying at rest on a rough horizontal surface. The coefficient of friction between the ground and sphere is μ. The maximum value of F, so that the sphere will not slip, is equal to

View SolutionA uniform solid sphere A of mass m is rolling without sliding on a a smooth horizontal surface. It collides elastically and head - on with another stationary hollow sphere B of the same mass and radius. Assuming friction to be absent everywhere, the ratio of the kinetic energy of B to that of A just after the collision is
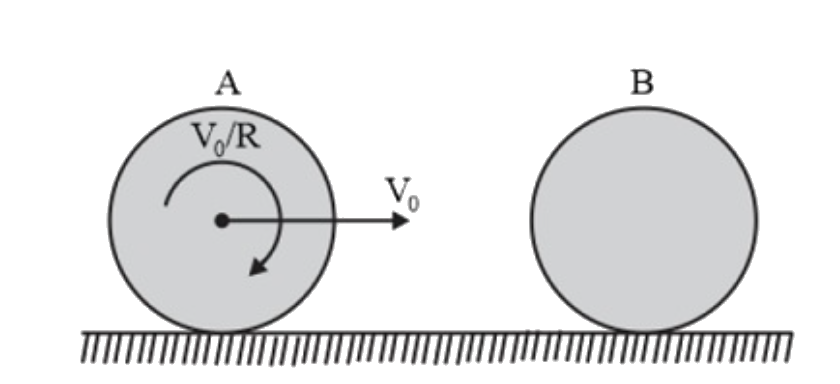
View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
View SolutionA block is kept on a rough horizontal surface as shown. Its mass is 2 kg and coefficient of friction between block and surface (μ)=0.5. A horizontal force F is acting on the block. When

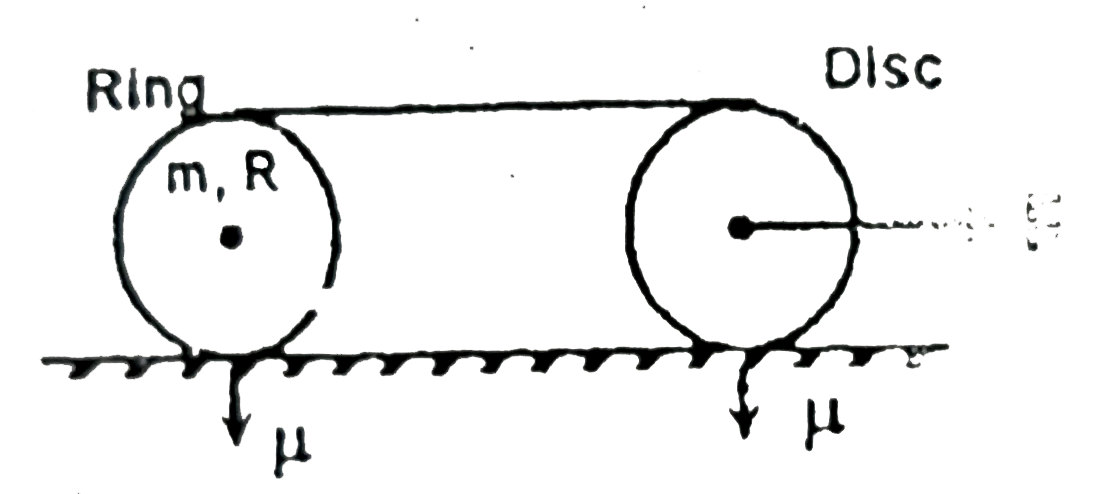
View SolutionIn the given situation disc and ring are connected with a string as shown in the figure. Both are placed on the rough surface of coefficient of friction μ. A force F is applied on the centre of disc horizontally. Then frictional force acting on the ring will be
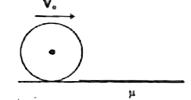
View SolutionA ring of mass m sliding on a smooth surface with velocity v0 enters rough surface with coefficient of kinetic friction μk, then
View Solution