Three point charges of +2q,+2qand−4q are placed at the corners A, B and C of an equilateral triangle ABC of side x. The magnitude of the electric dipole moment of this system is ?
2 qx
3√2qx
3 qx
2√3qx
The correct Answer is:D
To find the magnitude of the electric dipole moment of the system of three point charges located at the corners of an equilateral triangle, we can follow these steps:
Step 1: Identify the Charges and their Positions
We have three charges:
- Charge at A: +2q
- Charge at B: +2q
- Charge at C: −4q
These charges are placed at the corners of an equilateral triangle ABC with side length x.
Step 2: Break Down the Charges into Dipoles
We can treat the charges +2q at points A and B as forming a dipole with the charge −4q at point C. To analyze the dipole moments, we can consider the following:
- The dipole moment →P1 formed by the charge at A and the charge at C.
- The dipole moment →P2 formed by the charge at B and the charge at C.
Step 3: Calculate Individual Dipole Moments
The dipole moment →P is given by the formula:
→P=q⋅d
where q is the charge and d is the distance between the charges.
For dipole P1 (between +2q at A and −2q at C):
P1=2q⋅x
For dipole P2 (between +2q at B and −2q at C):
P2=2q⋅x
Step 4: Determine the Direction of the Dipoles
The direction of the dipole moment is from the negative charge to the positive charge. Therefore, both dipoles P1 and P2 point towards the center of the triangle.
Step 5: Calculate the Resultant Dipole Moment
Since both dipoles are at an angle of 60∘ to each other (the angle in an equilateral triangle), we can use the formula for the resultant of two vectors:
P=√P21+P22+2P1P2cos(60∘)
Substituting P1=P2=2qx and cos(60∘)=12:
P=√(2qx)2+(2qx)2+2(2qx)(2qx)(12)
=√4q2x2+4q2x2+4q2x2
=√12q2x2=2√3qx
Final Result
Thus, the magnitude of the electric dipole moment of the system is:
2√3qx
We have three charges:
- Charge at A: +2q
- Charge at B: +2q
- Charge at C: −4q
We can treat the charges +2q at points A and B as forming a dipole with the charge −4q at point C. To analyze the dipole moments, we can consider the following:
- The dipole moment →P1 formed by the charge at A and the charge at C.
- The dipole moment →P2 formed by the charge at B and the charge at C.
The dipole moment →P is given by the formula:
→P=q⋅d
where q is the charge and d is the distance between the charges.
P1=2q⋅x
P2=2q⋅x
The direction of the dipole moment is from the negative charge to the positive charge. Therefore, both dipoles P1 and P2 point towards the center of the triangle.
Since both dipoles are at an angle of 60∘ to each other (the angle in an equilateral triangle), we can use the formula for the resultant of two vectors:
P=√P21+P22+2P1P2cos(60∘)
P=√(2qx)2+(2qx)2+2(2qx)(2qx)(12)
=√4q2x2+4q2x2+4q2x2
=√12q2x2=2√3qx
Thus, the magnitude of the electric dipole moment of the system is:
2√3qx
Similar Questions
Electric charges q,q,–2q are placed at the corners of an equilateral triangle ABC of side l. The magnitude of electric dipole moment of the system is
View SolutionEqual charges q are placed at the vertices A and B of an equilatral triangle ABC of side a. The magnitude of electric field at the point C is
View Solution
Knowledge Check
Electric charges q,q,–2q are placed at the corners of an equilateral triangle ABC of side l. The magnitude of electric dipole moment of the system is
AqlB√3qlCzeroD4ql
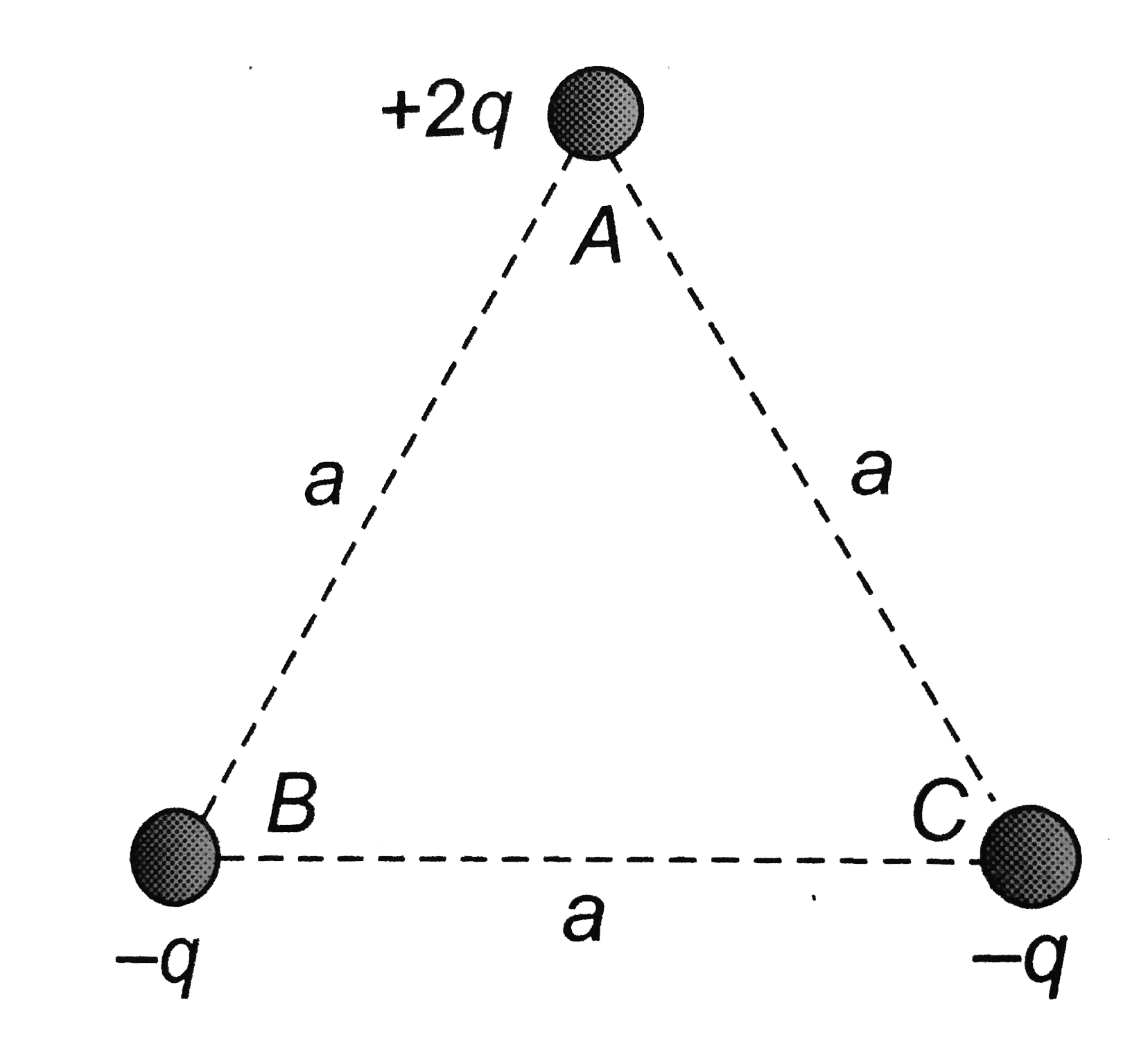
Three charges of (+2q),(−q) and (−q) are placed at the corners A,B and C of an equilateral triangle of side a as shown in the adjoining figure. Then the dipole moment of this combination is
View SolutionThree charges 2q,−q,and−q are located at the vertices of an equilateral triangle. At the center of the triangle,
View SolutionFour charges of +q, +q +q and +q are placed at the corners A, B, C and D of s square. The resultant force on the charge at D
View SolutionThree point charges q are placed at three vertices of an equilateral triangle of side a. Find magnitude of electric force on any charge due to the other two.
View SolutionThree points charges of 1C,2Cand3C are placed at the corners of an equilateral triangle of side 100 cm. Find the work done to move these charges to the corners of a similar equilateral triangle of side 50 cm.
View SolutionThree points charges of 1C,2Cand3C are placed at the corners of an equilateral triangle of side 100 cm. Find the work done to move these charges to the corners of a similar equilateral triangle of side 50 cm.
View SolutionFour charges of +q, +q +q and +q are placed at the corners A, B, C and D of s square. The resultant force on the charge at D
View Solution
