A ball having velocity v towards the right and having angular velocity clockwise approaches the wall. It collides elastically with wall and moves towards the left . Ground and wall are frictionless. Select the correct statement about the angular velocity of the ball after the collision .
It will be anti - clockwise
It becomes zero
Angular speed decreases
It will be clockwise
The correct Answer is:D
To solve the problem, we need to analyze the situation step by step:
Step 1: Understand the Initial Conditions
The ball is moving towards the right with a velocity v and has an angular velocity that is clockwise.
Hint: Identify the direction of both linear and angular velocities before the collision.
Step 2: Analyze the Collision
The ball collides elastically with the wall. In an elastic collision, both momentum and kinetic energy are conserved. However, since the wall is frictionless, we need to focus on how the collision affects the ball's linear and angular velocities.
Hint: Recall the properties of elastic collisions and how they affect velocities.
Step 3: Determine the Linear Velocity After Collision
After the collision, the ball moves towards the left with the same speed v (but in the opposite direction). This is due to the elastic nature of the collision.
Hint: Remember that the speed remains the same in an elastic collision, but the direction changes.
Step 4: Analyze the Effect on Angular Velocity
Since the wall and ground are frictionless, there is no tangential force acting on the ball during the collision. The normal forces exerted by the wall act through the center of the ball, which means they do not create any torque about the center of the ball.
Hint: Consider how torque is related to angular acceleration and how forces act on the ball.
Step 5: Conclusion on Angular Velocity
Because there is no torque acting on the ball (the tangential torque is zero), there is no angular acceleration. Therefore, the angular velocity of the ball remains unchanged in magnitude and direction. Since it was initially clockwise, it will still be clockwise after the collision.
Hint: Recall the relationship between torque, angular acceleration, and angular velocity.
Final Answer
The angular velocity of the ball after the collision remains in the clockwise direction.
Correct Statement: The angular velocity of the ball after the collision remains clockwise.
The ball is moving towards the right with a velocity v and has an angular velocity that is clockwise.
The ball collides elastically with the wall. In an elastic collision, both momentum and kinetic energy are conserved. However, since the wall is frictionless, we need to focus on how the collision affects the ball's linear and angular velocities.
After the collision, the ball moves towards the left with the same speed v (but in the opposite direction). This is due to the elastic nature of the collision.
Since the wall and ground are frictionless, there is no tangential force acting on the ball during the collision. The normal forces exerted by the wall act through the center of the ball, which means they do not create any torque about the center of the ball.
Because there is no torque acting on the ball (the tangential torque is zero), there is no angular acceleration. Therefore, the angular velocity of the ball remains unchanged in magnitude and direction. Since it was initially clockwise, it will still be clockwise after the collision.
The angular velocity of the ball after the collision remains in the clockwise direction.
Similar Questions
A small ball is projected horizontally between two large blocks. The ball is given a velocity Vms−1 and each of the large blocks move uniformly with a velocity of 2Vms−1. The ball collides elastically with the blocks. If the velocity of the blocks do not change due to the collision, then find out the velocity of the ball after the 2nd collision.
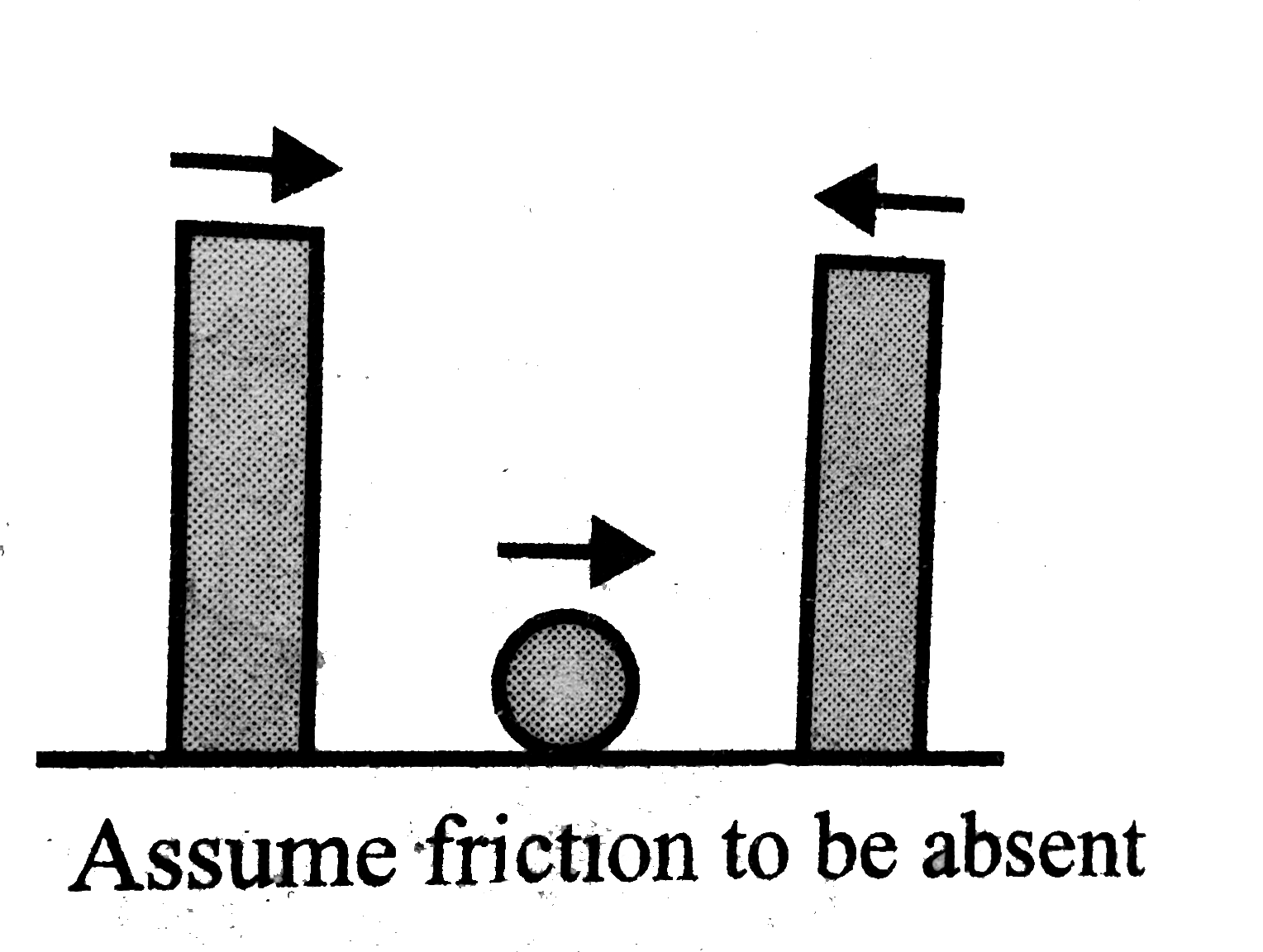
View SolutionA small ball of mass m collides with as rough wal having coeficient of friction μ at an angle θ with the normal to the wall. If after collision the ball moves wilth angle α with the normal to the wall and the coefficient of restitution is e, then find the reflected velocity v of the ball just after collision.

View Solution
Knowledge Check
A ball of mass m moving with a speed 2v0 collides head-on with an identical ball at rest. If e is the coefficient of restitution, then what will be the ratio of velocity of two balls after collision?
A1−e1+eBe−1e+1C1+e1−eDe+1e−1A ball of mass m moving with a speed 2v0 collides head-on with an identical ball at rest. If e is the coefficient of restitution, then what will be the ratio of velocity of two balls after collision?
A1−e1+eB1+e1−eCe−1e+1De+1e−1
A heavy ball of mass 2M moving with a velocity v0 collides elastically head on with a cradle of three identical ball each of mass M as shown in figure. Determine the velocity of each ball after collision.

View SolutionA particle of mass m moving at a velocity v strikes with the wall at an angle α with the wall and leaves ball making same angle with the wall. Choose the correct statemet (s) from the following.
View SolutionA sphere is moving on a smooth surface with angular velocity ω and linear velocity v. If collides elastically with another identical sphere B kept at rest. Neglecting friction everywhere, let VA and ωA be linear and angular velocities of sphere A after the impact and let VB and ωB be the corresponding parameters for spehre B. Then
View SolutionA ball moving with a velocity v hits a massive wall moving towards the ball with a velocity a. An elastic impact lasts for time △t
View SolutionIf a ball strickes with a velocity u1 at the wall which itself is approaching it with a velocity u2 then find the velocity of the ball after collision with the wall.
View SolutionA ball rolls without sliding over a rough horizontal floor with velocity v0=7m/s towards a smooth vertical wall. If coefficient of restitution between the wall and the ball is e=0.7. Calculate velocity v of the ball after the collision.
View Solution
