With two resistance in the two gaps of a metre bridge the balance was found to be 1/3 m from the zero end. When a resistance is connected in series with the smaller of the two resistance, the point is shifted to 2/3 m from the same end, then are
4,2
2,4
Both (a) and (b)
Neither (a) nor (b)
The correct Answer is:B
To solve the problem, we will use the principles of a meter bridge and the concept of a balanced Wheatstone bridge.
1. Understanding the Setup:
We have a meter bridge with two resistances R1 and R2 placed in its gaps. The balance point is initially at 13 m from the zero end. This means that the lengths of the bridge wire on either side of the galvanometer are 13 m and 23 m.
2. Applying the Wheatstone Bridge Principle:
According to the principle of the Wheatstone bridge, we have:
R1R2=xL−x
where x is the length from the zero end (which is 13 m) and L is the total length of the bridge (1 m). Thus, we can write:
R1R2=1323=12
From this, we can express R2 in terms of R1:
R2=2R1(Equation 1)
3. Introducing the 6 Ohm Resistor:
When a 6 Ohm resistor is connected in series with the smaller resistance R1, the effective resistance becomes R′1=R1+6. The new balance point is now at 23 m from the zero end.
4. Applying the Wheatstone Bridge Principle Again:
Now, we apply the Wheatstone bridge principle again:
R′1R2=2313=2
Substituting R′1:
R1+6R2=2
Rearranging gives us:
R1+6=2R2(Equation 2)
5. Substituting Equation 1 into Equation 2:
Now, we substitute R2=2R1 from Equation 1 into Equation 2:
R1+6=2(2R1)
Simplifying this gives:
R1+6=4R1
Rearranging gives:
6=4R1−R1
6=3R1
Thus, we find:
R1=2Ω
6. Finding R2:
Now, substituting R1 back into Equation 1:
R2=2R1=2×2=4Ω
Final Answer:
The values of the resistances are:
- R1=2Ω
- R2=4Ω
We have a meter bridge with two resistances R1 and R2 placed in its gaps. The balance point is initially at 13 m from the zero end. This means that the lengths of the bridge wire on either side of the galvanometer are 13 m and 23 m.
According to the principle of the Wheatstone bridge, we have:
R1R2=xL−x
where x is the length from the zero end (which is 13 m) and L is the total length of the bridge (1 m). Thus, we can write:
R1R2=1323=12
From this, we can express R2 in terms of R1:
R2=2R1(Equation 1)
When a 6 Ohm resistor is connected in series with the smaller resistance R1, the effective resistance becomes R′1=R1+6. The new balance point is now at 23 m from the zero end.
Now, we apply the Wheatstone bridge principle again:
R′1R2=2313=2
Substituting R′1:
R1+6R2=2
Rearranging gives us:
R1+6=2R2(Equation 2)
Now, we substitute R2=2R1 from Equation 1 into Equation 2:
R1+6=2(2R1)
Simplifying this gives:
R1+6=4R1
Rearranging gives:
6=4R1−R1
6=3R1
Thus, we find:
R1=2Ω
Now, substituting R1 back into Equation 1:
R2=2R1=2×2=4Ω
The values of the resistances are:
- R1=2Ω
- R2=4Ω
Similar Questions
Two resistances are connected in the two gaps of a meter bridge. The balance point is 20cm from the zero end. When a resistance 15Ω is connected in series with the smaller of two resistance, the null point+ shifts to 40cm. The smaller of the two resistance has the value.
View SolutionTwo resistances are connected in the two gaps of a meter bridge. The balance point is 20cm from the zero end. When a resistance 15Ω is connected in series with the smaller of two resistance, the null point+ shifts to 40cm. The smaller of the two resistance has the value.
View Solution
Knowledge Check
Two resistances are connected in the two gaps of a meter bridge. The balance point is 20cm from the zero end. When a resistance 15Ω is connected in series with the smaller of two resistance, the null point+ shifts to 40cm. The smaller of the two resistance has the value.
A3B6C9D12Two resistances R1=100±3ΩandR2=200±4Ω are connected in series . Find the equivalent resistance of the series combination.
A(66.7±1.8)ΩB(66.7±4.0)ΩC(66.7±3.0)ΩD(66.7±7.0)Ω
Two resistances are connected in two gaps of a meter bridge. The balance point is 20cm from the zero end. A resistance of 15Ω is connected in series with the smaller of the two. The null point shifts to 40cm. The value of the smaller resistance in Ω is
View SolutionTwo unknown resistances are connected in two gaps of a meter-bridge. The null point is obtained at 40 cm from left end. A 30Ω resistance is connected in series with the smaller of the two resistances, the null point shifts by 20 cm to the right end. The value of smaller resistance in Ω is
View SolutionThe resistance in the two arms of the meter bridge are 5Ω and RΩ, respectively. When the resistance R is shunted with an equal resistance, the new balance point is 1.6l1.
The resistance R is
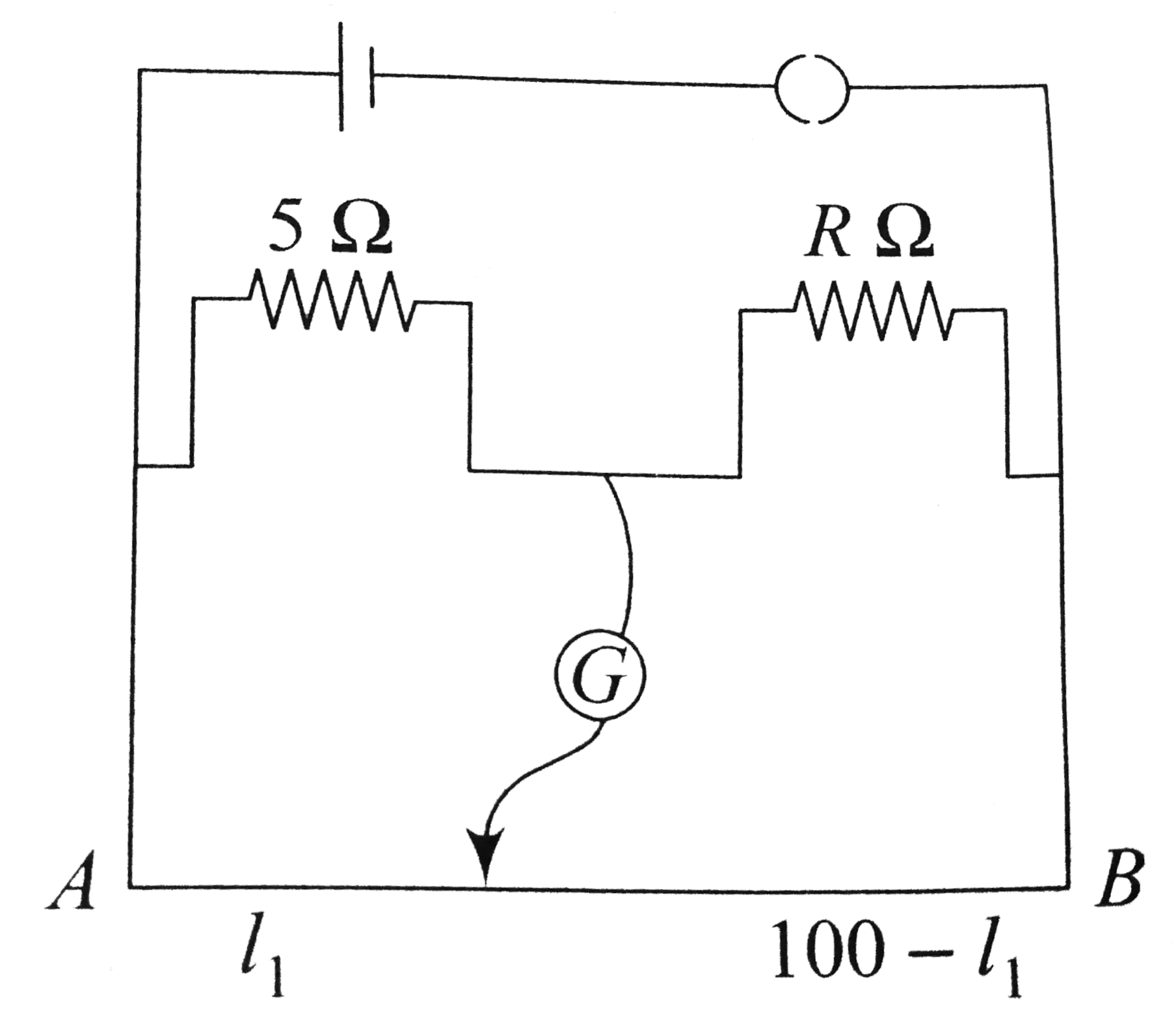
View SolutionThe resistance in the two arms of the meter bridge are 5Ω and RΩ, respectively. When the resistance R is shunted with an equal resistance, the new balance point is 1.6l1.
The resistance R is

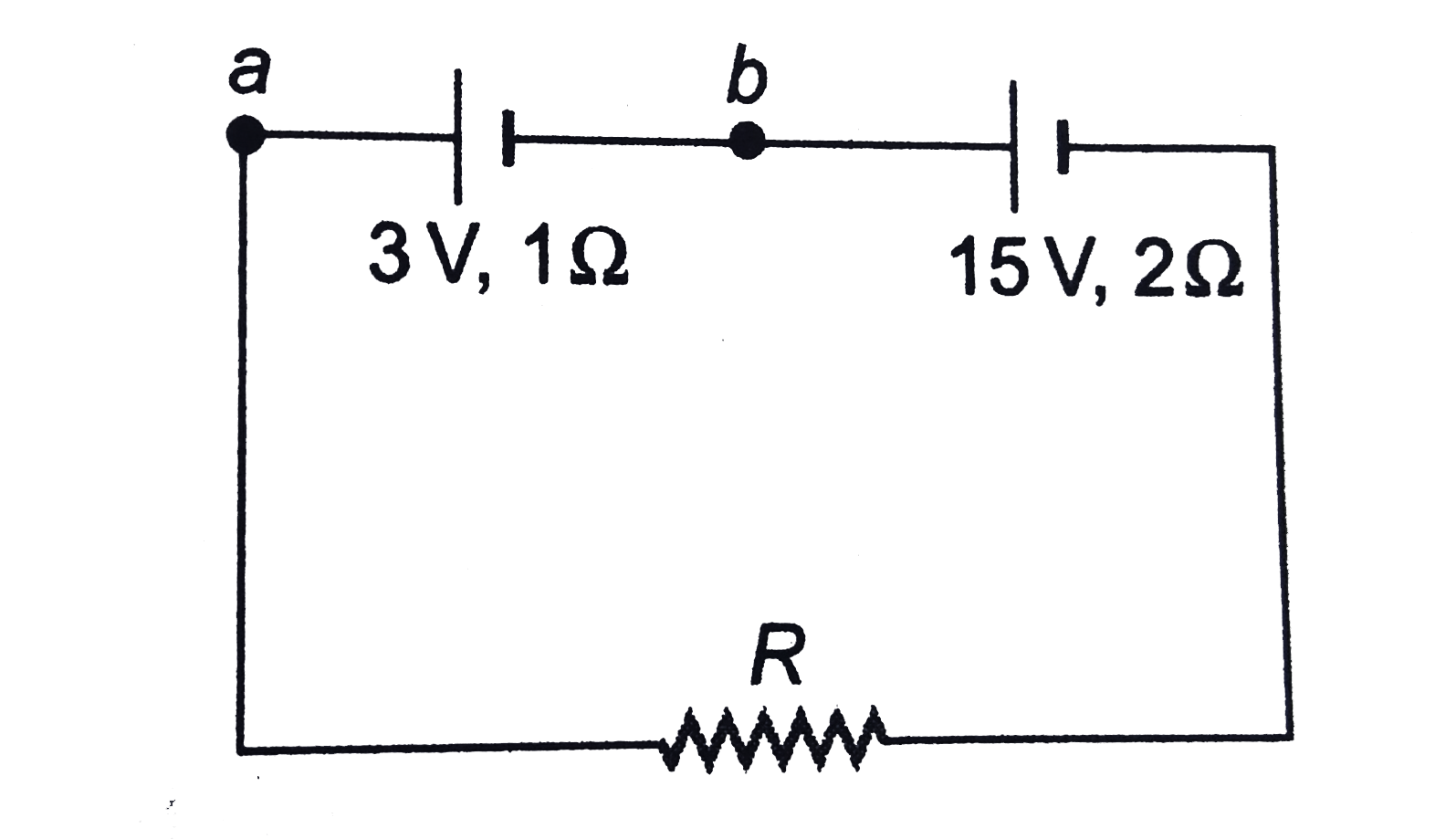
View SolutionTwo batteries one of the emf 3V, internal resistance 1Ω and the other of emf 15V, internal resistance 2Ω are connected in series with a resistance R as shown. If the potential difference between points a and b is zero, the resistance R in Ω is
View SolutionIn a meter-bridge experiment with a resistance R1 in left gap and a resistance X in a right gap. null point is obtained at 40cm from the left emf. With a resistance R2 in the left gap, the null point is obtainned at 50cm from left hand. Find the position of the left gap is containing R1 and R2 (i) in series and (ii) in parallel.
View Solution
