Mercury is completely filled in a rectangular take of height 72 cm. The atmospheric pressure at the place is 72 cm. of Hg. Find the distance in cm of point of application from bottom of tank of the net force , on the inner surface of the side vertical wall of tank.
32 cm
16 cm
74 cm
42 cm
The correct Answer is:A
To solve the problem, we need to find the distance from the bottom of the tank to the point of application of the net force on the inner surface of the side vertical wall of the tank. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Pressure at Depth
The pressure at a depth x in a fluid is given by:
P=Patm+ρgx
where:
- Patm is the atmospheric pressure (given as 72 cm of Hg),
- ρ is the density of mercury,
- g is the acceleration due to gravity,
- x is the depth from the surface of the fluid.
Step 2: Calculate the Force on a Differential Area
Consider a small horizontal strip at depth x with thickness dx and length L (the length of the tank). The differential area dA is:
dA=Ldx
The force dF acting on this differential area due to pressure is:
dF=P⋅dA=(Patm+ρgx)⋅(Ldx)
Step 3: Integrate to Find Total Force
To find the total force F on the wall, we integrate dF from the bottom of the tank (0 cm) to the top (72 cm):
F=∫720(Patm+ρgx)Ldx
Substituting Patm=ρg⋅72 (since 72 cm of Hg is equivalent to the pressure exerted by 72 cm of mercury):
F=L∫720(ρg⋅72+ρgx)dx
Step 4: Calculate the Integral
Calculating the integral:
F=L⋅ρg(72x+x22)720
Evaluating the limits:
F=L⋅ρg(72⋅72+7222)=L⋅ρg(5184+2592)=L⋅ρg⋅7776
Step 5: Find the Point of Application of Force
The point of application of the force can be found using the concept of torque. The torque τ about the bottom of the tank due to the force dF at depth x is:
dτ=dF⋅x=(Patm+ρgx)Ldx⋅x
Integrating this from 0 to 72 gives:
τ=∫720(Patm+ρgx)Lxdx
Step 6: Calculate the Torque Integral
Calculating the integral:
τ=L⋅ρg(72x2/2+x33)720
Evaluating the limits:
τ=L⋅ρg(72⋅722/2+7233)
Step 7: Relate Torque to Force and Distance
The point of application of the force from the bottom of the tank can be found using:
L0=τF
Substituting the values of τ and F calculated in previous steps.
Final Calculation
After performing the calculations, we find that the distance from the bottom of the tank to the point of application of the net force is:
Distance from bottom=30cm
The pressure at a depth x in a fluid is given by:
P=Patm+ρgx
where:
- Patm is the atmospheric pressure (given as 72 cm of Hg),
- ρ is the density of mercury,
- g is the acceleration due to gravity,
- x is the depth from the surface of the fluid.
Consider a small horizontal strip at depth x with thickness dx and length L (the length of the tank). The differential area dA is:
dA=Ldx
The force dF acting on this differential area due to pressure is:
dF=P⋅dA=(Patm+ρgx)⋅(Ldx)
To find the total force F on the wall, we integrate dF from the bottom of the tank (0 cm) to the top (72 cm):
F=∫720(Patm+ρgx)Ldx
Substituting Patm=ρg⋅72 (since 72 cm of Hg is equivalent to the pressure exerted by 72 cm of mercury):
F=L∫720(ρg⋅72+ρgx)dx
Calculating the integral:
F=L⋅ρg(72x+x22)720
Evaluating the limits:
F=L⋅ρg(72⋅72+7222)=L⋅ρg(5184+2592)=L⋅ρg⋅7776
The point of application of the force can be found using the concept of torque. The torque τ about the bottom of the tank due to the force dF at depth x is:
dτ=dF⋅x=(Patm+ρgx)Ldx⋅x
Integrating this from 0 to 72 gives:
τ=∫720(Patm+ρgx)Lxdx
Calculating the integral:
τ=L⋅ρg(72x2/2+x33)720
Evaluating the limits:
τ=L⋅ρg(72⋅722/2+7233)
The point of application of the force from the bottom of the tank can be found using:
L0=τF
Substituting the values of τ and F calculated in previous steps.
After performing the calculations, we find that the distance from the bottom of the tank to the point of application of the net force is:
Distance from bottom=30cm
Similar Questions
The volume of an air bubble becomes three times as it rises from the bottom of a lake to its surface. Assuming atmospheric pressure to be 75 cm of Hg and the density of water to be 1/10 of the density of mercury, the depth of the lake is
View SolutionA container of height 10 cm is filled with water. There is hole at bottom. Find the pressure difference between point A & B .
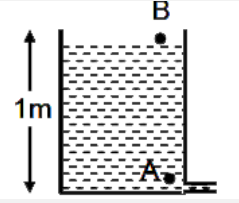
View SolutionThere are two holes one each along the opposite sides of a wide rectangular tank. The cross section of each hole is 0.01m2 and the vertical distance between the holes is one meter. The tank is filled with water. The net force on the tank in newton when water flows out of the holes is (density of water 1000kg/m3)
View SolutionA vessel of base area 100cm×60cm and height 200cm is completely filled with a liquid of density 1.1×103kgm−3.
(a) Ignoring the atmospheric pressure, find :
(i) the thrust at the bottom of the vessel,
(ii) the pressure at the bottom of the vessel,
(iii) The pressure at a depth of 5 cm from the free surface,
(iv) the net force experienced by a metal foil of area 10cm2 placed at a depth of 5 cm from the free surface,
(b) The thrust at the bottom of the vessel if the atmospheric pressure equal to 1×105Nm−2 is taken into account.
Take g=9.8ms−2 .
View SolutionWater is filled in a rectangular tank of size 3m×2m×1m. a) Find the total force exerted by the water on the bottom surface of the tank. b) Consider a vertical side of area 2m×1m. Take a horizontal strip of wide δx metre in this side, situated at a depth of x metre from the surface of water.Find the force by the water on this strip. c) Find the torque of the force calculate in part b) about the bottom edge of this side. d) Find the total force by the water on this side. e) Find the total torque by the water on the side about the bottom edge. neglect the atmospheric pressure and take =10ms−2.
View SolutionThe flat bottom of cylinder tank is silvered and water (μ=43) is filled in the tank upto a height h. A small bird is hovering at a height 3h from the bottom of the tank. When a small hole is opened near the bottom of the tank, the water level falls at the rate of 1 cm/s. The bird will perceive that his velocity of image is 1/x cm/sec (in downward directions) where x is
View Solution_S01_024_Q01.png)
Water and liquid is filled up behind a square wall of side l
Find out (a). Pressure at A, B and C
(b). Forces in part AB and BC
(c). Total force and point of application of force. (Neglect atmosphere pressure in every calculation.)
View SolutionWater and liquid are filled up behind a square wall of side. Find out
a. pressures at A,B and C
b. forces in part AB and BC
c. total force and point of application of force (neglect atmospheric pressure in every calculation)
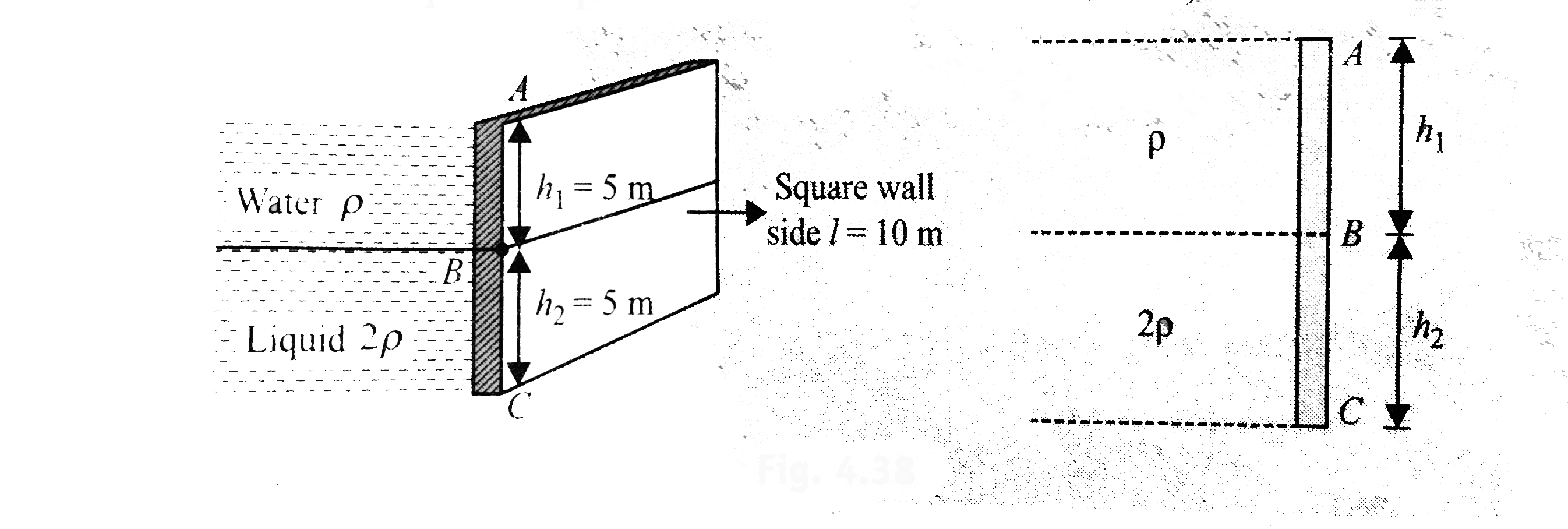
View SolutionA liquid of density ρ is filled upto a geight of 'h' in a container as shown in firgure. Base of the contaimer is a square of side L. Ignoring the atmospheric pressure find

(a) pressure force F1 on its base.
(b) torque of force F1 about an axis passing through C and perpendicular to plane of paper.
(c ) Pressure force F2 on the vertical side wall DC.
(d) torque of force F2 about the same axis mentioned in part (b).
(e) point of application of force F2
View SolutionFigure shows a large closed cylindrical tank containing water, Initially the air trapped above the water surface has a height h0and pressure 2p0 where p0is the atmospheric pressure. There is a hole in the wall of tank at a depth h1below the top from which water comes out. A long vertical tube is connected as shown. (a) Find the height h2 of the water in the long tube above the top initially. (b) Find the speed with which water comes out of hole.(c)Find the height of the water in the long tube above the top when the water stops coming out of the hole.

View Solution
